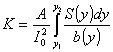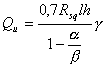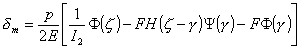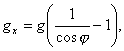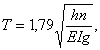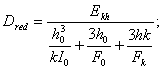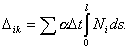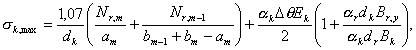|
|
ОРДЕНА ТРУДОВОГО КРАСНОГО
ЗНАМЕНИ ПОСОБИЕ (к СНиП II-22-81) Утверждено Москва Центральный институт
типового проектирования 1989 Рекомендовано к изданию научно-техническим советом ЦНИИСК им. Кучеренко Госстроя СССР. Пособие по проектированию
каменных и армокаменных конструкций (к СНиП II-22-81 „Каменные и армокаменные
конструкции. Нормы проектирования") /ЦНИИСК им. Кучеренко Госстроя СССР. -
М.: ВДПП Госстроя СССР, 1989. Приведены дополнительные
рекомендации по проектированию и расчету каменных и армокаменных конструкций, а
также примеры расчетов. Для инженерно-технических
работников проектных и строительных организаций. Табл. 56, ил. 97. При пользовании Пособием
следует учитывать утвержденные изменения строительных норм и правил и
государственных стандартов, публикуемые в журнале «Бюллетень строительной
техники", «Сборнике изменений строительных норм и правил" Госстроя
СССР и информационном указателе «Государственные стандарты СССР"
Госстандарта СССР. ПРЕДИСЛОВИЕПособие разработано на
основе „Руководства по проектированию каменных и армокаменных конструкций"
(М.: Стройиздат, 1974) и распространяется на проектирование каменных и
армокаменных конструкций жилых, общественных, промышленных и
сельскохозяйственных здание и сооружений, строящихся в летних и зимних условиях. Проектирование каменных
конструкции зданий, возводимых в зимнее время, производится в соответствии с
указаниями СНиП II-22-81 пп. [7.1-7.15] и разд. 8 настоящего Пособия. Текст СНиП II-22-81 в Пособии не приводится, но имеются ссылки на соответствующие пункты, таблицы, формулы и чертежи, которые указаны в квадратных скобках. Пособием следует пользоваться одновременно со СНиП II-22-81. Пособие разработано Отделом
прочности крупнопанельных и каменных зданий ЦНИИСК им. Кучеренко Госстроя СССР
(кандидаты техн. наук Г.Н. Брусенцов, С.А. Воробьева, А.А. Емельянов, В.А.
Камейко, П.Г. Лабозин, И.Т. Котов, Н.И. Левин, д-р техн. наук С.В.
Поляков, кандидаты техн. наук А.И. Рабинович, В.П. Хлебцов, д-р
техн. наук А.А. Шишкин. В подготовке примеров к Пособию принимали
участие инженеры (Э.М. Басаева, Л.М. Ломова, Е.Л. Степанова, Е.В.
Шенкаренко) при участии НИИ строительной физики (д-р техн. наук Ф.Л.
Ушков, канд. техн. наук А.И. Ананьев) и института Башкиргражданпроект
(В.А. Першин). Пункт 3.13 составлен по данным д-ра техн. наук Н.А.
Рохлина и А.М. Самедова (НИИСК Госстроя СССР). Подготовка рукописи к
изданию выполнена Г.Л. Брусенцовым, В.А. Камейко, П.Г. Лабозиным и А.Л.
Рабиновичем. 1.ОБЩИЕ ПОЛОЖЕНИЯ1.1. Настоящее Пособие
составлено в развитие СНиП II-22-81 и содержит методы
расчета и проектирования зданий и сооружений из каменных материалов. При проектировании каменных
и армокаменных конструкций следует соблюдать также требования соответствующих
нормативных документов, утвержденных или согласованных Госстроем СССР. Это указание относится, в
частности, к проектированию каменных и армокаменных конструкций зданий и
сооружений, подвергающихся динамическим воздействиям, а также предназначенных
для строительства в сейсмических районах, в условиях воздействия агрессивной
среды, систематических технологических температур выше 100° С, в зонах
распространения вечномерзлых, просадочных и набухающих грунтов и на
подрабатываемых территориях, к проектированию специальных видов каменных
конструкций (транспортных и гидротехнических сооружений, дымовых труб,
коллекторов и т. д.). 1.2. При проектировании
каменных и армокаменных конструкций необходимо, как правило, предусматривать
конструктивные решения, изделия и материалы, указанные в п. [1.2], и учитывать
требования пп. [1.3-1.6]. 1.3. Типовые проекты должны
предусматривать варианты конструктивных решений стен с учетом применения
изделий и материалов, указанных в п. [1.2]. Каменные конструкции следует
проектировать с наиболее полным использованием их несущей способности и
максимальным применением местных строительных материалов, запрещается
применение сплошной кирпичной кладки для наружных стен из полнотелого кирпича,
см. п. [1.2а]. Во избежание утолщения
наиболее нагруженных стен и столбов, где это необходимо по расчету прочности
конструкций, следует применять кирпич марок 150 и выше или усиление простенков
и столбов сетчатым армированием или железобетоном (комплексные конструкции). Выбор оптимальных
конструкций следует производить на основании приведенных затрат с учетом
стоимости материалов, трудовых затрат, транспорта, а также эксплуатационных
расходов, отдавая предпочтение индустриальным виброкирпичным конструкциям. 1.4. Проектами в необходимых
случаях следует предусматривать защиту каменных и армокаменных конструкций от
механических воздействий, а также от влияния влажностной или агрессивной среды
(защитные покрытия выступающих и особо подверженных увлажнению и внешним
воздействиям частей стены, облицовки, пароизоляционные и гидроизоляционные слои
и т. д.). Следует предусматривать
также защиту от коррозии стальных связей, закладных и соединительных деталей. 1.5. Кроме расчета конструкций законченного здания в условиях их совместной работы с другими элементами здания необходимо проверить расчетом прочность и устойчивость стен и других конструкций незаконченного здания в процессе возведения этих конструкций. Если по расчету устойчивость указанных конструкций окажется недостаточной, надлежит предусматривать временные крепления до устройства перекрытий или других конструкций, обеспечивающие их устойчивость. 1.6. При проверке прочности
и устойчивости стен, столбов, карнизов и других элементов в период возведения
зданий следует учитывать, что элементы перекрытий (балки, плиты и пр.)
укладываются по ходу кладки. Если условия возведения
запроектированных конструкций требуют особой последовательности работ,
выдерживания кладки или специальных конструктивных мероприятий, временных
креплений и т. д., об этом на чертежах должны быть сделаны специальные
указания. 1.7. При возведении
конструкций, расчетная несущая способность которых используется более чем на 80
%, следует производить систематический контроль прочности кирпича (камней) и
раствора. 2. МАТЕРИАЛЫ И ИЗДЕЛИЯОБЩИЕ ТРЕБОВАНИЯ2.1. Для возведения каменных
и армокаменных конструкций применяют искусственные и природные каменные
материалы в виде кирпича, камней, мелких и крупных блоков и панелей, а также
облицовочные и теплоизоляционные материалы, строительный раствор, бетон и
арматуру. 2.2. Искусственные и
природные каменные материалы, а также бетоны, применяемые для изготовления
камней, мелких и крупных блоков, должны удовлетворять требованиям ГОСТ
4.206-83 в части плотности, прочности, морозостойкости и других показателей
качества. 2.3. Предполагаемый срок
службы каменных материалов для наружной части стен и фундаментов и их проектные
марки по морозостойкости принимают при проектировании с учетом влажностного
режима помещений по указаниям, приведенным в пп. [2.3-2.5]. Влажностный режим
помещений принимается по СНиП II-3-79. 2.4. Доставляемые на
строительство каменные материалы должны иметь заводской паспорт, содержащий
сведения о пределе прочности (марке) и морозостойкости, а для легких и
теплоизоляционных материалов - и по их плотности (объемной массе). При
отсутствии паспорта строительная организация до применения этих материалов
должна провести необходимые испытания (ГОСТ 6427-75 и ГОСТ
8462-85). КИРПИЧ И КАМНИ КЕРАМИЧЕСКИЕ2.5. Кирпич изготовляют
полнотелым или пустотелым, с вертикальными пустотами, а керамические камни
только пустотелыми (ГОСТ 530-80), Масса кирпича и камней не должна превышать
4,3 кг. Применение пустотелых кирпича и камней в наружных стенах повышает их
сопротивление теплопередаче и позволяет уменьшить толщину стен. Во избежание заполнения сквозных
пустот раствором ширина их не должна превышать 12 мм, а диаметр круглых пустот
должен быть менее 16 мм. КИРПИЧ И КАМНИ СИЛИКАТНЫЕ2.6. Кирпич и камни
силикатные (ГОСТ 379-79) имеют такие же размеры и массу, как и керамические.
Силикатный кирпич толщиной 65 мм изготовляют полнотелым, а утолщенный кирпич -
пустотелым или полнотелым с пористыми заполнителями. Силикатные камни
изготовляют только пустотелыми с вертикальными круглыми пустотами диаметром
30-32 мм, замкнутыми с верхней стороны. При применении силикатных кирпича и
камней следует учитывать указания п. [1.3]. КИРПИЧ И КАМНИ КЕРАМИЧЕСКИЕ И СИЛИКАТНЫЕ ЛИЦЕВЫЕ2.7. Кирпич и камни лицевые (ГОСТ 7484-78
и ГОСТ 379-79) применяют для облицовки наружных стен здании и сооружений,
выполняемой одновременно с кладкой. Изготовляют кирпичи и камни с гладкой или
рельефной лицевой поверхностью, естественного цвета или окрашенными в массе
путем ввода в сырьевые материалы различных добавок. КАМНИ БЕТОННЫЕ СТЕНОВЫЕ2.8. Камни бетонные стеновые
(ГОСТ 6133-84),
сплошные и пустотелые, лицевые и рядовые изготовляют из тяжелых и легких
бетонов на цементных, силикатных и гипсовых вяжущих. Применяют их для несущих и
ограждающих конструкций зданий различного назначения. При применении камней,
изготовленных на силикатных и гипсовых вяжущих, следует учитывать указания п.
[1-3]. БЛОКИ ИЗ ЯЧЕИСТЫХ БЕТОНОВ СТЕНОВЫЕ МЕЛКИЕ2.9. Блоки из ячеистых
бетонов стеновые мелкие (ГОСТ 21520-76) применяют для кладки стен зданий
различного назначения с нормальным температурно-влажностным режимом. Применение
блоков в наружных стенах помещений с влажным режимом допускается при условии
нанесения на внутренние поверхности стен пароизоляционного покрытия. Применять
блоки для наружных стен помещений с мокрым режимом, а также для стен подвалов и
цоколей не допускается, см. п. [1.3]. БЛОКИ СТЕНОВЫЕ БЕТОННЫЕ2.10. Блоки стеновые
бетонные, изготовляемые из тяжелого бетона, легкого бетона на пористых
заполнителях, плотного силикатного бетона и автоклавного ячеистого бетона (ГОСТ
19010-82), применяют для наружных и внутренних стен зданий различного
назначения. Применение блоков из ячеистого бетона в наружных стенах помещений с
влажным режимом допускается при условии нанесения на внутренние поверхности
стен пароизоляционного покрытия. Применение блоков из ячеистого бетона не
допускается для стен помещений с мокрым режимом или при средне- и
сильноагрессивной степенях воздействия среды на конструкции, а также в стенах
цокольного этажа и технического подполья. КАМНИ СТЕНОВЫЕ ИЗ ГОРНЫХ ПОРОД2.11. Камни стеновые из
горных пород (ГОСТ 4001-84)
предназначены для кладки стен, перегородок и других частей зданий и сооружений.
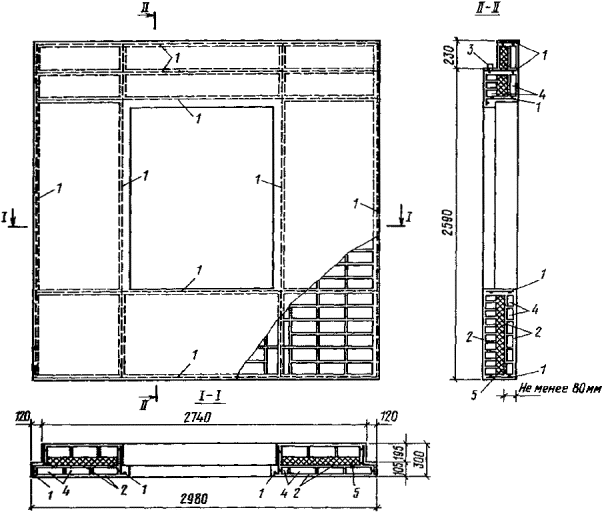
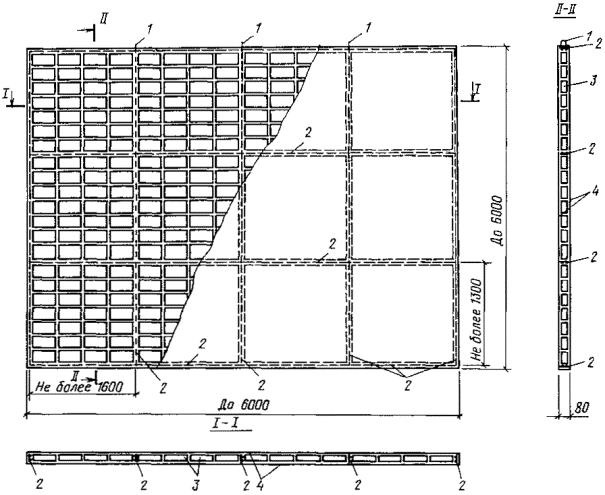
Масса одного камня не должна превышать 40 кг. ПАНЕЛИ И БЛОКИ СТЕНОВЫЕ ИЗ КИРПИЧА
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Возраст раствора, сут. |
Прочность раствора, %, при
температуре твердения, °С |
||||||||||
|
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
|
1 |
1 |
4 |
6 |
10 |
13 |
18 |
23 |
27 |
32 |
38 |
43 |
|
2 |
3 |
8 |
12 |
18 |
23 |
30 |
38 |
45 |
54 |
63 |
76 |
|
3 |
5 |
11 |
18 |
24 |
33 |
47 |
49 |
58 |
66 |
75 |
85 |
|
5 |
10 |
19 |
28 |
37 |
45 |
54 |
61 |
70 |
78 |
85 |
95 |
|
7 |
15 |
25 |
37 |
47 |
55 |
64 |
72 |
79 |
87 |
94 |
99 |
|
10 |
23 |
35 |
48 |
58 |
68 |
75 |
82 |
89 |
95 |
100 |
- |
|
14 |
31 |
45 |
60 |
71 |
80 |
85 |
92 |
96 |
100 |
- |
- |
|
21 |
42 |
58 |
74 |
85 |
92 |
96 |
100 |
103 |
- |
- |
- |
|
28 |
52 |
68 |
83 |
96 |
100 |
104 |
- |
- |
- |
- |
- |
Примечания: 1. Данные таблицы относятся
к растворам, твердеющим при относительной влажности воздуха 50-60 %.
2. При применении растворов,
изготовленных на шлакопортландцементе и пуццолановом портландцементе, следует
учитывать замедление нарастания их прочности при температуре твердения ниже 15 °С.
Величина прочности этих растворов определяется умножением значений, приведенных
в таблице, на коэффициенты: 0,3 - при температуре твердения 0°С; 0,7 - при 5 °С;
0,9 - при 9 °С и 1,0 - при 15 °С и выше.
3. Для промежуточных значений
температуры твердения и возраста раствора прочность его определяется
интерполяцией.
4. Растворы по плотности (в
сухом состоянии) подразделяют на тяжелые - плотностью 1500 кг/м3 и
легкие - плотностью менее 1500 кг/м3. Тяжелые растворы изготовляют с
применением плотных, а легкие - пористых заполнителей.
2.22. Прочность раствора зависит от температуры твердения. При температуре твердения, отличающейся от 20±2°С, прочность раствора, %, в возрасте 28 сут следует принимать по табл. 1.
3. ФИЗИКО-МЕХАНИЧЕСКИЕ СВОЙСТВА
НЕАРМИРОВАННОЙ И АРМИРОВАННОЙ
КАМЕННОЙ КЛАДКИ
ОСНОВНЫЕ ПОЛОЖЕНИЯ
3.1. Каменная кладка
является неоднородным телом, состоящим из камней и швов, заполненных раствором.
Этим обусловливаются следующие особенности ее работы: при сжатии кладки усилие
передается неравномерно вследствие местных неровностей и неодинаковой плотности
отдельных участков затвердевшего раствора. В результате камни подвергаются не
только сжатию, но также изгибу и срезу.
3.2. Характер разрушения кладки и степень влияния многочисленных факторов на ее прочность объясняются особенностями ее напряженного состояния при сжатии. Разрушение обычной кирпичной кладки при сжатии начинается с появления отдельных вертикальных трещин, как правило, над и под вертикальными швами, что объясняется явлениями изгиба и среза камня, а также концентрацией растягивающих напряжений над этими швами.
3.3. Первые трещины в
кирпичной кладке появляются при нагрузках меньших, чем разрушающие, причем
обычно отношение m = Ncrc:Nu тем меньше, чем слабее
раствор (Ncrc - нагрузка, соответствующая моменту
появления трещин; Nu - разрушающая нагрузка). Так например, для
кладок на растворах марок:
50 и выше m = 0,7 - 0,8
10 и 25 m = 0,6 - 0,7
0; 2 и 4 m = 0,4 - 0,6
Момент появления первых трещин
зависит от качества выполнения горизонтальных швов и плотности применяемого
раствора. При неровных швах и растворах малой объемной массы (например, с
заполнителем в виде легкого песка) величина m может быть меньше
приведенных значений.
В кладках из крупноразмерных
изделий (например, из некоторых видов высокопустотных керамических камней,
камней из ячеистого бетона) наступает хрупкое разрушение, первые трещины
появляются при нагрузках 0,85-1 от разрушающей.
3.4. На прочность кладки при
сжатии влияют следующие факторы: прочность камня; размеры камня; правильность
формы камня; наличие пустот в пустотелых камнях; прочность раствора;
удобоукладываемость (подвижность) раствора; упругопластические свойства
(деформативность) затвердевшего раствора; качество кладки; перевязка кладки;
сцепление раствора с камнем; степень заполнения раствором вертикальных швов
кладки.
Прочность камня и раствора, размеры и форма камня имеют решающее значение для прочности кладки.
Большое влияние на прочность
кладки оказывает сопротивление кирпича растяжению и изгибу. Поэтому
государственный стандарт устанавливает требования к прочности кирпича как при
сжатии, так и при изгибе. Прочность кирпича при изгибе оказывает меньшее
влияние на прочность кладки, чем при сжатии.
Прочность кладки при сжатии
вследствие возникновения в ней сложного напряженного состояния значительно
меньше сопротивления камня сжатию. Например, прочность кирпичной кладки при
слабых растворах составляет всего лишь 10-15 %, а при прочных растворах -
30-40% прочности кирпича.
Прочность кладки из камней
неправильной формы во много раз меньше прочности камня и составляет даже для
кладки на прочном растворе марки 100 из рваного бута высокой прочности лишь 5-8
% прочности камня. При одной и той же прочности камня и раствора прочность
кладки из постелистого бута в 1,5 раза, а из камня правильной формы в 3,5 раза
выше кладки из рваного бута.
3.5. Высокого качества
кладки, равномерного и плотного заполнения швов раствором можно достичь,
применяя вибрирование кирпичной кладки. В этом случае прочность кирпичной
кладки в 1,5-2 раза выше прочности обычной кладки среднего качества.
Качество заполнения шва в
значительной степени зависит от подвижности применяемого раствора. Прочность
кладки, выложенной на подвижных (пластичных) растворах, выше прочности кладки
на жестких растворах. В связи с этим в растворах применяют пластифицирующие и
водоудерживающие добавки в виде извести, глины и других материалов.
3.6. Перевязка кирпичной
кладки на прочном растворе при осевом сжатии несущественно влияет на прочность
кладки, если она выполняется не реже чем в каждом шестом ряду. Однако при
кладке, выполняемой в зимних условиях или в сейсмических районах, при большой
внецентренности приложения нагрузки и больших местных нагрузках рекомендуется
применять цепную перевязку.
3.7. Сцепление раствора с
камнем и качество заполнения вертикальных швов влияют на прочность кладки при
сжатии. Монолитность, трещиностойкость кладки и ее сопротивление усилиям изгиба
и растяжения при неравномерной осадке фундаментов, изменении температуры и
прочее существенно зависит от указанных факторов.
ПРЕДЕЛ ПРОЧНОСТИ КЛАДКИ
3.8. Предел прочности всех
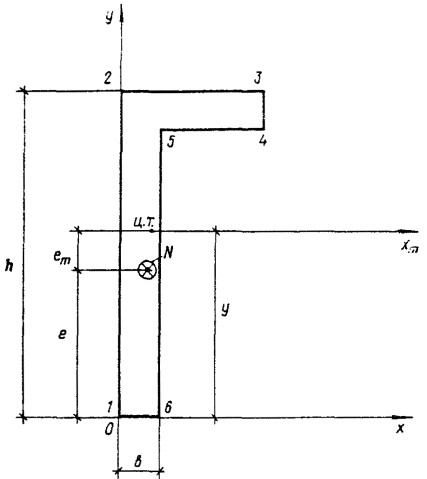
видов кладок при кратковременном загружении определяется по формуле профессора
Л.И. Онищика:
где Ru - предел прочности кладки при
сжатии;
R1 - предел прочности камня при
сжатии;
R2 - предел прочности раствора
(кубиковая прочность).
Коэффициент А характеризует
максимально возможную, так называемую «конструктивную», прочность кладки.
Действительно, из формулы (1)
следует, что при R2®¥ Ru=АR1.
Коэффициент А (конструктивный
коэффициент) определяется по формуле
![]() , (2)
, (2)
где R1 выражен в кгс/см2.
Величины коэффициентов a, b, m и n
приведены в табл. 2.
Таблица 2
|
Кладка |
а |
b |
m |
n |
|
Кирпичная (высота ряда от 5 до 15 см) и из крупных
кирпичных блоков |
0,2 |
0,3 |
1,25 |
3 |
|
Из сплошных камней правильной формы (высота ряда
18-29 см) |
0,15 |
0,3 |
1,1 |
2,5 |
|
То же, из пустотелых камней |
0,15 |
0,3 |
1,5 |
2,5 |
|
Из сплошных крупных блоков (высота ряда 60 см и
более) |
0,09 |
0,3 |
См. примеч. |
|
|
Из рваного бутового камня (для кладки в возрасте 3
мес) |
0,2 |
0,25 |
2,5 |
8,0 |
Примечание. При определении прочности
кладки из сплошных легкобетонных крупных блоков принимается коэффициент А =
0,8, а из крупных блоков тяжелого бетона А = 0,9.
Если прочность кирпича при
изгибе меньше предусмотренной ГОСТ 530-80, то конструктивный коэффициент А для
кладки определяется по формуле
![]() , (3)
, (3)
где Rub - прочность кирпича при
изгибе.
Коэффициент g
применяют при определении прочности кладки на растворах низких марок (25 и
ниже). Эти коэффициенты принимают равными при:
R2>R2,1 g=1
R2<R2,1
![]() , (4)
, (4)
Для кладки из кирпича и
камней правильной формы R2,1=0,04R1; g0=0,75;
для бутовой кладки R2,1=0,08R1; g0=0,25.
Формула (1) установлена для случаев, когда качество
кладки соответствует уровню массового строительства, а применяемые растворы
достаточно подвижны и удобоукладываемы. Если эти условия не соблюдаются, то
влияние ряда факторов учитывается применением дополнительных коэффициентов к
значениям Ru, вычисленным по формуле (1). В случае, например, применения жестких,
неудобных для кладки цементных растворов (без добавки глины или извести),
растворов на шлаковом или другом легком песке, а также сильно сжимаемых (в
возрасте до 3 мес.) известковых растворов пределы прочности кладки понижаются
на 15% по сравнению с вычисленными по формуле
(1). В среднем на 15% понижается предел прочности кладки из пустотелых
крупных бетонных блоков по сравнению с пределом прочности кладки из сплошных
крупных блоков той же марки. Предел прочности кладки из постелистого бута на 50
% выше кладка из рваного бута.
3.9. Предал
прочности вибрированной кирпичной кладки, в которой обеспечено плотное и
равномерное заполнение швов раствором, значительно (в 1,5-2 раза) выше обычное
кладки.
3.10. Предел прочности кладка
и бетона зависит также от длительности загружения. Пределом длительного
сопротивления кладки или бетона Rg является максимальное
напряжение, которое может выдержать кладка или бетон неограниченное время без
разрушения. Величина Rg для тяжелых бетонов равна
0,8-0,85Ru, а для ячеистых бетонов неавтоклавного твердения
0,55-0,60Ru. Для кирпичной кладки на прочных растворах, марок 50
и выше ориентировочно Rg=0,8Ru, марок 10 к 25-0,7Ru и для кладок на известковом растворе 0,6Ru.
Следует
однако учитывать, что после длительного периода твердения раствора под
нагрузкой (более года) вследствие его пластических деформации происходит
выравнивание поверхности раствора в швах кладки, что уменьшает местные
концентрации напряжений и позволяет повысить расчетное сопротивление кладки на
15 %, см. п. [3.11г].
РАСЧЕТНЫЕ СОПРОТИВЛЕНИЯ
3.11. Принятое в стандарте
СЭВ 384-76 понятие нормативного сопротивления материалов, связанное с
контрольной или браковочном их характеристикой, устанавливаемой
государственными стандартами на материалы, не применяется к кладке, так как она
является композитным материалом и ее прочность не установлена стандартами.
При установлении расчетных
сопротивлений для каменных конструкций принята следующая система коэффициентов.
Коэффициент изменчивости прочности кирпичной кладки на основании статистических
данных принят равным С=0,15, а условное нормативное сопротивление Rn=Ru(1-2С)=0,7Ru, при этом обеспеченность
величины С равна 0,98. Вероятное понижение прочности кладки по сравнению с
уровнем, принятым в нормах, учитывается делением Rn на коэффициент 1,2, а другие
второстепенные факторы, не учитываемые расчетом, и дефекты (ослабление кладки
пустошовкой, гнездами, небольшие отклонения столбов и стен от вертикали и т.
п.) - на коэффициент 1,15. Таким образом, дополнительный коэффициент надежности
для кирпичной кладки принят равным 1,2´1,15=1,4 и расчетное
сопротивление R=0,7Ru/1,4=0,5Ru.
Расчетные сопротивления кладки сжатию из всех видов каменных и бетонных изделий приведены в табл. [2-9], пп. [3.1-3.14]. Средние ожидаемые пределы прочности кладки могут быть определены, в случае необходимости, умножением расчетных сопротивлений на коэффициенты безопасности, приведенные в п. [3.20].
3.12. Расчетные сопрот0
асимметрии r:
![]() , (5)
, (5)
где smin и smax - соответственно наименьшее
и наибольшее значения напряжений в кладке, возникающих от нормативных
статических и повторяющихся нагрузок.
|
r£0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
D=0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
Примечание. Коэффициенты D даны для кладок в 28-дневном возрасте.
СЦЕПЛЕНИЕ РАСТВОРА С КАМНЕМ И
ПРОЧНОСТЬ КАМЕННЫХ КЛАДОК
ПРИ РАСТЯЖЕНИИ И СРЕЗЕ
3.14. Прочность кладки при
растяжении и срезе зависит, главным образом, от сцепления раствора с камнем.
Прочность сцепления зависит от многих факторов, например, вида и состава
раствора, прочности и усадки раствора, скорости поглощения камнем воды, чистоты
поверхности камня, условий твердения раствора в кладке (температуры и влажности
воздуха), содержания посторонних примесей в камне и растворе и др.
3.15. При осевом растяжении
и растяжении при изгибе различают случаи сопротивления неперевязанных
(горизонтальных швов) и перевязанных сечений. Во втором случае разрушение может
происходить по ступенчатому сечению, т. е. по горизонтальным и вертикальным
швам или же по плоскому сечению, т. е., по вертикальным швам и целому камню.
3.16. Расчетные сопротивления кладки из кирпича и камней правильной формы осевому растяжению, растяжению при изгибе, а также при срезе принимают по пп. [3.15 и 3.16].
ДЕФОРМАЦИИ КЛАДКИ
3.17. Каменная кладка
является упругопластическим телом. Ее деформации зависят от длительности
приложения нагрузки или же скорости загружения кладки.
Различают:
а) упругие (или мгновенные)
деформации. К этим деформациям близки также деформации кладки, получаемые при
очень быстром загружении (несколько секунд от начала загружения до разрушения
образца). Зависимость между напряжениями и деформациями в этом случае близка к
прямолинейной;
б) кратковременные
деформации, соответствующие обычной в лабораторных условиях длительности
испытаний (до одного часа);
в) деформации при длительном
загружении в течение многих лет.
3.18. Полная относительная
деформация кладки є0 (без учета усадки) может быть выражена формулой
є0
= єel
+ єg, (6)
где єel
- упругая относительная деформация кладки;
єg
- относительная деформация при длительном приложении нагрузки.
При этом єg
может быть представлена в виде
єg= є1g+ є2g, (7)
где є1g
- пластическая деформация, возникающая при кратковременной нагрузке (т. е. при
нагрузке длительностью до 1 ч);
є2g
- деформация ползучести.
Пластическая деформация є1g
бетонов и кладок на прочном растворе при напряжениях σ£0,5Ru обычно не превышает 15 %
упругой деформации. Полная предельная деформация (при t®¥) є0 обычно в 2-4
раза больше єel.
3.19. Относительные
деформации кладки є при кратковременной нагрузке могут определяться при любых
напряжениях по формуле
где a
- упругая характеристика кладки, принимаемая по п. [3.21];
s
- напряжение, при котором определяется є;
Ru - средний предел прочности кладки, определяемый по п.[3.20].
Упругие характеристики кладки
с сетчатым и продольным армированием принимаются по п. [3.20].
Значения
коэффициента В приведены в табл. 4.
Таблица 4
|
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
В×10-3 |
0,11 |
0,22 |
0,35 |
0,50 |
0,67 |
0,86 |
1,11 |
1,43 |
1,87 |
2,64 |
3.20. Относительные полные деформации сжали (без учета усадки) при
длительном приложении нагрузки, включающие кратковременные деформации и
деформации ползучести, определяются во п. [3.23].
3.21. Модули упругости и
деформации кладку из природных камней допускается принимать по специальным
указаниям, составленным на основе результатов экспериментальных исследовании,
утвержденным госстроями союзных республик.
3.22. В
зависимости от конструктивного решения менее благоприятные результаты могут
быть получены как при кратковременных, так и при длительных нагрузках.
Например, в многослойной конструкции наиболее напряженный при кратковременной
нагрузке слой может с течением времени загружаться, а менее напряженный
нагружаться. Поэтому необходимо учитывать деформации, возникающие как при
кратковременной, так и при длительной нагрузках.
3.23. Зависимость между
напряжениями и деформациями криволинейна, модуль деформации не является
величиной постоянной (черт. 1).

Черт. 1. Модуль деформация
1 - начальный модуль деформаций (модуль
упругости) Е0 = tga0; 2 -
касательный модуль деформаций Еtan=
tga1=![]() ; 3 - средний (секущий) модуль деформаций Е = tga=
; 3 - средний (секущий) модуль деформаций Е = tga=![]()
Различают:
Е0 - начальный
модуль деформации (модуль упругости) кладки, соответствующий малым напряжениям
(s<0,3Ru). Beличина E0 определяется по формуле
E0=a
Ru, (9)
касательный модуль деформаций
(действительный)
Etan=ds/dє; (10)
средний (секущий) модуль деформаций
E=s/є; (11)
При зависимости между
напряжениями и деформациями по формуле
(8) модули деформаций определяются по формуле
Etan=Е0(1-s/1,1Ru). (12)
3.24. Прb расчете
конструкции с учетом длительного приложения нагрузке наиболее важной
характеристикой является предельная полная деформация кладки єu
(соответствующая t®¥). Значение этой
величины различно для разных видов бетонов и кладок. Для практических расчетов
значения єu нормированы и определяются умножением упругой
деформации s/Е0 на
коэффициенты n, зависящие от вида кладка
(см. п. [3.23]). Нормированные значения n относятся к деформациям при
напряжениях s£0,5 Ru. При этих значениях напряжений деформации ползучести
в основном развиваются в течение первого года после загрузки и затем постепенно
затухают. При больших напряжениях деформации ползучести затухают медленнее, а
при напряжениях, превышающих предел длительного сопротивления Rg, скорость деформаций с течением времени увеличивается и наступает разрушение.
Скорость нарастания деформаций зависит от вида материалов и качества кладки,
возраста кладки и момента ее загрузки, размеров сечения кладки и определяется
по п.[3.23].
Деформации усадки кладки из
глиняного обожженного кирпича и керамических камней не учитываются. Деформации
усадки кладки из силикатного кирпича и камней, бетонных камней и блоков
принимаются по п. [3.26].
ОБЪЕМНАЯ МАССА (ПЛОТНОСТЬ) КЛАДКИ
3.25. Нормативная объемная
масса кладки, принимаемая при расчете каменных конструкций на прочность,
приведена в табл. 5. При расчете должна
учитываться также собственная масса штукатурке равной 15 кг/м2. В
случае применения мокрой штукатурки ее толщина, при отсутствии специальных
данных, принимается равной 1,5 см; нормативная объемная масса штукатурки из
цементного или смешанного раствора - 1800 кг/м3, а из известкового
раствора - 1600 кг/м3.
|
Кладка |
Нормативная объемная
масса, кг/м3 |
|
Сплошная из полнотелого кирпича |
1800 |
|
Из пустотелого, пористо-дырчатого или пористого
кирпича при объемной массе кирпича, кг/м3: |
|
|
1450 |
1550 |
|
1300 |
1400 |
|
Из пустотелых керамических камней при высоте камня
138 мм при объемной массе камня, кг/м3: |
|
|
1450 |
1500 |
|
1300 |
1300 |
|
Из легкобетонных камней с щелевидными пустотами
(пустотность 26%) при объемной массе, кг/м3: |
|
|
1400 |
1100 |
|
1600 |
1230 |
|
Из легкобетонных трехпустотных камней со сквозными
пустотами с засыпкой шлаком, керамзитом и т.п. (пустотность камня 35%,
объемная масса засыпки 1000 кг/м3) при объемной массе бетона, кг/м3: |
|
|
1400 |
1300 |
|
1600 |
1420 |
|
Бутовая из известняка при объемной массе известняка
2200-2500 кг/м3 |
2100 |
|
Из крупных блоков из тяжелого бетона |
2400 |
|
Из крупных блоков из легкого или ячеистого бетона |
Принимается равной объемной массе бетона с учетом
его влажности |
Примечания: 1. Нормативная объемная
масса кладки принята с учетом возможного ее изменения в пределах ±10%,
что учитывается коэффициентами перегрузки. Поэтому нормативная объемная масса,
применяемая при расчете на прочность, может отличаться от объемной массы, принимаемой
при теплотехнических расчетах.
2.
Толщина штукатурки не включается в расчетное сечение при определении несущей
способности элемента.
3.
В табл. 5 указана объемная масса кладок, выполненная на тяжелых растворах,
имеющих объемную массу 1800 кг/м3.
4. РАСЧЕТ ЭЛЕМЕНТОВ КАМЕННЫХ КОНСТРУКЦИЙ
ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ПЕРВОЙ ГРУППЫ
(ПО НЕСУЩЕЙ СПОСОБНОСТИ)
ОБЩИЕ ПОЛОЖЕНИЯ
4.1. Расчет каменных и
армокаменных конструкций по предельным состояниям первой группы (потеря несущей
способности, потеря устойчивости формы, потеря устойчивости положения)
производится, как правило, на воздействие расчетных нагрузок.
4.2. Расчет каменных и
армокаменных конструкций незаконченных зданий и сооружений производится на
воздействие нормативной ветровой нагрузки, а для других нагрузок принимаются их
расчетные значения.
4.3. Влияние длительного
приложения нагрузки на прочность каменной кладки учитывается при назначении
расчетных сопротивлений п.[3.11г] и расчете гибких элементов по указаниям пп.
[4.1 и 4.7].
4.4. Сцепление раствора с
кирпичом и камнем отличается большой изменчивостью и зависит от многих
случайных величин. Поэтому расчет неармированных каменных конструкций
производится без учета сопротивления кладки растяжению и изгибу по
неперевязанным сечениям (например, по горизонтальным швам), за исключением
случаев расчета на сейсмические нагрузки.
4.5. Расчет каменных
конструкций на внецентренное сжатие производится без учета сопротивления
растянутой зоны сечения. При больших эксцентриситетах, см. п. [4.8],
производится дополнительная проверка сечения по образованию и раскрытию трещин;
в этом случае условно учитывается сопротивление кладки растяжению по
неперевязанному сечению как косвенная характеристика возможного раскрытия
трещин.
4.6. Сопротивление кладки
растяжению по неперевязанному сечению учитывается при расчете кладки на
сейсмические воздействия. В этом случае при выполнении кладки должны
соблюдаться специальные правила, повышающие надежность сцепления в соответствии
со СНиП II-7-81. Прочность сцепления проверяется при этом контрольными
испытаниями в лабораторных и натурных условиях.
ЦЕНТРАЛЬНО И ВНЕЦЕНТРЕННО СЖАТЫЕ ЭЛЕМЕНТЫ
4.7. Расчет элементов
неармированных каменных конструкций при центральном и внецентренном сжатии
производится по указаниям и формулам, приведенным в пп. [4.1-4.11].
При назначении расчетной
высоты стены, если ее опорами являются перекрытия и примыкающие к ней
поперечные стены, разрешается учитывать опирание стены по контуру (по трем или
четырем сторонам), при выполнении следующих условий:
а) по четырем сторонам, если
стена ослаблена проемами не более чем на 40 % как по вертикальному, так и по
горизонтальному сечению. При ослаблении вертикального сечения более чем на 40%,
но менее чем на 60 % разрешается учитывать опирание по четырем сторонам, при условии
компенсации дополнительного (сверх 40 %) ослабления кладки - горизонтальными
железобетонными поясами с жесткостью, равной жесткости пояса кладки высотой На
- 0,4Н, где На - высота проема. Закрепление по четырем сторонам
разрешается учитывать, если m=H:l ³ 0,5 (l - длина и H -
высота участка стены, определяемая по указаниям п.
4.8);
б) если стена ослаблена
проемами более, чем это указано в подп. «а», или опирается по трем сторонам
вместе с тем m=H:l ³ 1, разрешается учитывать
опирание стены по трем сторонам.
К случаям опирания стены по
трем сторонам относятся, например:
участок стены от места
примыкания внутренней стены к наружной до ближайшего дверного проема;
вертикальные участки
самонесущей стены промышленного или общественного здания, примыкающей и
закрепленной связями к поперечной раме железобетонного или металлического
каркаса;
в) если связь между
продольными и поперечными стенами осуществляется только перевязкой кладки, то
опирание стены по трем или четырем сторонам разрешается учитывать при условии,
если разница в напряжениях этих стен, определяемая без учета перераспределения
напряжений между ними, не превышает 30 % расчетного сопротивления сжатию кладки
(без учета сетчатого армирования, если оно имеется). При большей разнице в
напряжениях стены следует соединять железобетонными или защищенными от коррозии
металлическими связями не менее чем в трех уровнях по высоте этажа. В каркасных
зданиях учет опирания стен по контуру разрешается при условии, если стена надежно
связана со стойками и верхним ригелем каркаса.
Расчетная высота стен l0c,
если перекрытие (или другая горизонтальная конструкция) может рассматриваться
как неподвижная в горизонтальном направлении опора стены с учетом опирания по
контуру, определяется в зависимости от отношения m = Н:l из
условия l0c=1,2l0/mÖK £ l0 , где Н - высота этажа; l -
длина участка стены; l0 - расчетная высота стены,
принимаемая по п. [4.3] без учета опирания стены по боковым граням.
Величины K при
закреплении участка стены по четырем сторонам равны:
m=Н:l 0,5 0,6 0,7 0,8 0,9 1 и более
K 6,25 5,14 4,52 4,2 4,08 4
Величины K при закреплении участка
стены по трем сторонам равны:
m=Н:l 1 1,2 1,4 1,6 1,8 2 2,5 3 4 5 и более
K 1,44 1,14 0,95 0,84 0,76 0,7 0,61 0,56 0,52 0,5
4.8. Указанное в п. [4.3а]
шарнирное опирание принимается в зданиях с неподвижными жесткими опорами, см.
п. [6.7], при опирании на стену перекрытий без заделки в кладку опорных
участков плит, настилов, балок, прогонов и т. п., а также при деревянных
перекрытиях независимо от заделки их на опорных участках.
Величина H при
железобетонных сборных или монолитных перекрытиях, заделанных на опорах в
кладку, принимается равной высоте этажа за вычетом толщины железобетонной
плиты, настила или панели перекрытия. В остальных случаях H
принимается равной высоте этажа.
В одноэтажных зданиях за
нижнюю опору принимается уровень отмостки или пола, если он конструктивно
связан со стеной или находится ниже уровня земли.
4.9. Если в стене или столбе
имеются горизонтальные или наклонные борозды (одна или две с обеих сторон
элемента в одном сечении), не превышающие в сумме по глубине 1/3 толщины стены,
а по высоте - 1/10 высоты этажа, то при определении гибкости элемента следует
приближенно принимать условную высоту этажа H1 = 1,1H. Наличие
этих борозд может не учитываться при определении j, если они
расположены в уровне междуэтажного перекрытия (в зданиях с неподвижными
опорами).
Если борозды имеют большую
указанных глубину или высоту, при определении гибкости принимается толщина стены
в месте ее ослабления. При расчете ослабленного сечения на внецентренное сжатие
эксцентриситет принимается относительно оси ослабленного сечения.
КОСОЕ ВНЕЦЕНТРЕННОЕ СЖАТИЕ
4.10. Расчет элементов
неармированных каменных конструкций при косом внецентренном сжатии
(внецентренное сжатие в двух направлениях) производится по указаниям п. [4.12].
СМЯТИЕ (МЕСТНОЕ СЖАТИЕ)
4.11. Расчет сечений при смятии (местном сжатии) следует производить на нагрузки, приложенные к части площади сечения (при опирании на кладку ферм, балок, прогонов, перемычек, панелей перекрытий, колонн и др.).
Несущая способность кладки
при смятии определяется с учетом характера распределения давления по площади
смятия.
Расчет на смятие следует
производить с учетом возможного опирания конструктивных элементов (балок,
лестничных маршей и др.) в процессе возведения здания на свежую или оттаивающую
зимнюю кладку.
4.12. Расчет сечений при
смятии производится по указаниям и формулам пп. [4.13-4.17]. Конструктивные
требования к участкам кладки, загруженным местными нагрузками, приведены в пп.
[6.40- 6.43].
Кроме расчета на смятие
опорные узлы должны быть рассчитаны также на центральное сжатие по указаниям
пп. [6.44 и 6.45].
4.13. При необходимости
повышения несущей способности опорного участка кладки при смятии могут
применяться следующие конструктивные мероприятия:
а) сетчатое армирование
опорного участка кладки, см. пп. [4.30 и 4.31], а также пп. 5.12-5.17;
б) опорные распределительные
плиты;
в) распределительные пояса
при покрытиях больших пролетов, особенно в зданиях с массовым скоплением людей
(кинотеатры, залы клубов, спортзалы и т. п.);
г) устройство пилястр;
д) комплексные конструкции
(железобетонные элементы, забетонированные в кирпичную или каменную кладку);
е) выполнение из полнотелого
кирпича верхних 4-5 рядов кладки в местах опирания элементов на кладку.
4.14. При местных краевых
нагрузках, превышающих 80 % расчетной несущей способности кладки при смятии,
следует под элементом, создающим местную нагрузку, усиливать кладку сетчатым
армированием. Сетки должны иметь ячейки размером не более 100´100 мм и диаметр стержней не
менее 3 мм.
В местах приложения местных
нагрузок, в случаях, когда усиление кладки сетчатым армированием является
недостаточным, следует предусматривать укладку распределительных плит толщиной,
кратной толщине рядов кладки, но не менее 14 см, армированных по расчету двумя
сетками с общим количеством арматуры не менее 0,5% в каждом направлении.
При краевом опорном давлении
однопролетных балок, прогонов, ферм и т. п. более 100 кН укладка опорных
распределительных плит (или поясов) является обязательной также и в том случае,
если это не требуется по расчету. При таких нагрузках толщину распределительных
плит следует принимать не менее 22 см.
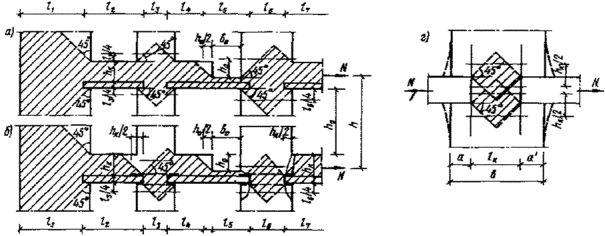
4.15. Расчет кладки на смятие под
опорами свободно лежащих изгибаемых элементов (балок, прогонов и т. п.), см. п.
[4.17], производится в зависимости от фактической длины опоры а1, и
полезной длины а0, черт. 2. Эпюра
напряжений под концом балки принимается по трапеции (при а1<а0)
или по треугольнику (при а1³а0). Допускается
также приближенно принимать треугольную эпюру с основанием а0=а1, если длина опорного конца балки
меньше ее высоты.

Черт. 2. Распределение
напряжений под концом балки
а - эпюра напряжений -
трапеция (а1<а0);
б - то же, треугольник (а1³а0)
Полезная длина опоры
определяется по формуле
Краевые напряжения при эпюре
в виде в виде трапеции:
![]() ; (14)
; (14)
![]() ; (15)
; (15)
где ![]() ; (16)
; (16)
при эпюре в виде
треугольника:
smax=2s0 (17)
где ![]() ; (18)
; (18)
а0 - полезная
длина опоры;
Q - опорная реакция балки;
b -
ширина опорного участка балки, плиты настила или распределительной плиты под
концом балки;
а1 - длина опоры
балки;
с - коэффициент постели при
смятии кладки под концом балки;
a
- угол наклона оси балки на опоре.
Коэффициент постели с
определяется по формулам:
для затвердевшей кладки
![]() , (19)
, (19)
где Ru - временное сопротивление
(средний предел прочности) сжатию кладки, определяемое по формуле [3] п.
[3.20];
для свежей кладки
![]() , (20)
, (20)
Ru1 -
временное сопротивление сжатию кладки на растворе марки 2.
При определении tga принимается, что балка
опирается на шарнир, расположенный посередине опорною конца. При неразрезных
балках промежуточные опоры принимаются расположенными по оси соответствующих столбов
или стен.
Для свободно лежащих балок
при равномерной нагрузке
![]() , (21)
, (21)
где l - пролет балки;
EI -
жесткость балки.
Для других нагрузок углы
поворота см. в табл. 8.1.2 «Справочника проектировщика», т. 1
(расчетно-теоретический). - М.: Стройиздат, 1972.
В п. [4.13, формула (17)]
величины коэффициента полноты эпюры давления и площади Ас при эпюре
напряжений под концом балки в виде трапеции определяются до формулам:
 , Ас=а1b.
(22)
, Ас=а1b.
(22)
При треугольной эпюре
напряжений:
y=0,5; Ас=а1b (23)
Если по
расчету несущая способность опорного участка при свежей кладке недостаточна,
рекомендуется установка временных стоек, поддерживающих концы балок.
4.16. При
загружении кладки на смятие в двух направлениях учет ее работы производится
путем перемножения коэффициентов полноты эпюр напряжений, см. п. [4.13].
Для нахождения формы
распределения величины местных сжимающих напряжений под опорой перемычки в
поперечном направлении определяется полезная ширина опоры b0 из условия равенства нулю
суммы моментов относительно середины ширины опорной площадки перемычки. Тангенс
угла поворота перемычки вокруг продольной оси определяется из формулы (13), в которой a0 заменяется на b0 , а b на a1. Коэффициент полноты эпюры
давления от местной нагрузки определяется из отношения объема эпюры давления к
объему smaxAc.
4.17. Расчет кладки на смятие
под опорами однопролетных балок или настилов с заделанными опорами производится
по п. [6.46], при этом величина эксцентриситета е0 определяется по
формуле
![]() , (24)
, (24)
где М - изгибающий момент в
заделке;
Q -
опорная реакция балки.
При равномерно распределенной
нагрузке на балку или плиту настила
![]() . (25)
. (25)
Для других нагрузок величины
изгибающих моментов в заделке см. в табл. 8.1.2 «Справочника проектировщика».
4.18. При расчете сечений
кладки, расположенных под распределительной плитой, нагрузка на плиту от
установленной на нее балки (фермы и т. п.) без фиксирующей прокладки
принимается в виде сосредоточенной силы, равной опорной реакции опирающегося на
плиту элемента. Точка приложения силы принимается на расстоянии l/3l1, но не более 7 см от
внутреннего края плиты (черт. 3, а).
При наличии прокладки,
фиксирующей положение опорного давления, расстояние от точки приложения
сосредоточенной силы до внутреннего края прокладки определяется по указаниям
настоящего пункта, причем в этом случае l1 - длина прокладки (черт. 3, б).
Распределительная плита
должна быть рассчитана на местное сжатие, изгиб и скалывание при действии
местной нагрузки, приложенной сверху, и реактивного давления кладки снизу. При
расчете распределительной плиты сосредоточенная сила заменяется нагрузкой,
равномерно распределенной по площади смятия, имеющей ширину b
опорного участка опирающегося на плиту элемента, и длину, равную 2u
где u - расстояние от внутреннего края плиты или
фиксирующей прокладки до оси нагрузки (см. черт. 3).
Черт. 3. Схема нагрузок и
напряжения при расчете опорной плиты
а - опирание балки без
фиксирующей прокладки;
б - опирание балки с
прокладкой
4.19. Если нагрузка передается на кладку через распределительные
устройства (например, через железобетонную или металлическую плиту), то эти
устройства в расчетной схеме заменяются поясом кладки или столбом), имеющим
размеры в плане те же, что и распределительные устройства с эквивалентной по
жесткости высотой, вычисленной по формуле
 , (26)
, (26)
где Ер - модуль
упругости материала распределительного устройства (для железобетонных
распределительных устройств Ер = 0,85 Еb, где Еb - начальный модуль упругости бетона);
Ip - момент инерции распределительного устройства;
Е - модуль упругости кладки,
принимаемый E=0,5E0;
d -
размер распределительного устройства в направлении, перпендикулярном
направлению распределения.
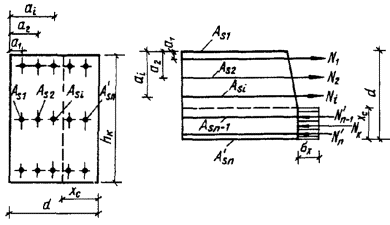
4.20. Напряжения в кладке под
распределительными устройствами определяются по формулам, приведенным в табл. 6.
В этих формулах s -
радиус влияния местной нагрузки, равный
![]() , (27)
, (27)
где Н -
расстояние от уровня, в котором приложена местная нагрузка, до рассчитываемого
сечения.
При расчете сечения под
распределительным устройством Н=Н0, а в расположенных ниже сечениях
Н=Н0+Н1, где H1 - расстояние от нижней
поверхности распределительного устройства до рассчитываемого сечения.
4.21. Если к
распределительному устройству приложено несколько сосредоточенных и
распределенных местных нагрузок, эпюры напряжений по его подошве могут быть
определены как сумма эпюр, соответствующих каждой из этих нагрузок.
Распределенные нагрузки могут заменяться несколькими эквивалентными по величине
сосредоточенными силами.
4.22. Размеры
распределительного устройства (или размеры основания конструкции, создающей
местную нагрузку) должны выбираться такими, чтобы выполнялось условие
smax£0,8xRu, (28)
где x - определяется по формуле
[19] п. [4.14];
Ru - по формуле [3] п. [3.20].
Длина распределительной плиты
(если она не ограничена размерами сечения кладки) должна быть больше длины
опорного конца балки l1, установленной на плиту без
фиксирующей прокладки (черт. 4, a). Для определения
необходимой длины распределительной плиты l1 принимается, что
равнодействующая давления от конца балки на плиту приложена непосредственно на
торце балки (черт. 4, б).
|
Схема приложения нагрузки
и распределения напряжений |
Формулы применимы в
сечениях, где |
Напряжения s0 и si |
|
|
a1
и a2 > |
|
|
|
a<s |
|
|
3.
|
a1<s
|
|
|
4.
|
a1<s
a2,0<a2 |
a0=1,125a1;
|
|
5.
|
a1<s
a2³s0
для затвердевшей кладки: u³12 см>H для свежей или оттаявшей
кладки: u³24 см³2H Нагрузка q
погашает растягивающие напряжения под плитой |
a0=0,15s+0,85a1; s0=0,4a1+0,6s |
|
6.
|
а1 и а2
больше s+b/2 и одновременно b<2s |
|
|
7.
|
а1 и а2
> s+b/2 и одновременно b>2s |
|
|
|
и одновременно b<2s |
|
|
9.
|
и одновременно b<2s |
|
Примечание: q – нагрузка; d –
толщина элемента.
Этим учитывается возможность,
например, неравномерной осадки опор. С учетом места расположения
равнодействующей этого давления по формулам, приведенным в табл. 6, определяется эпюра давления от распределительной
плиты на кладку. При этом величина ординаты эпюры давления s1
(см. черт. 4, б) на краю
распределительной плиты, примыкающей к незагруженной части кладки, не должна
превышать расчетного сопротивления кладки сжатию R. Если по конструктивным
соображениям длина опорной плиты не может быть увеличена, то необходимо
увеличить ее ширину.
4.23. В зоне кладки, примыкающей
к площади смятия, расположенной на краю стены, а также при установке
распределительной плиты, под которой условно принимается равномерная эпюра
напряжения, возникают горизонтальные растягивающие усилия. С точностью,
достаточной для практических расчетов, эпюра растягивающих напряжений может
быть представлена в виде треугольника с максимальной ординатой в уровне
приложения местной нагрузки и подошвы плиты, см. черт. 5.
Черт. 4. Расчетная схема узла
опирания балки на кладку
а - нагрузка и
напряжения при расчете кладки на местное сжатие под опорной плитой; б -
нагрузка и напряжения при определении длины опорной плиты
Черт. 5. Распределение
растягивающих напряжений в кладке при смятии
а - при отсутствии
распределительной плиты; б - при установке распределительной плиты; 1 -
распределительная плита; 2 – кладка
Высота растянутой зоны b определяется по формуле
где а - длина загруженного
участка;
v = a/l;
l - длина
элемента, включающая загруженный участок.
Наибольшая
ордината эпюры растягивающих напряжений st,max определяется по формуле
st,max=0,4q/(9,6v2 - 1,7 v + 1), (30)
где q - величина нагрузки, МПа
(кгс/см2), равномерно распределенной по площади местного сжатия.
При v<0,2 следует
принимать этот коэффициент равным 0,2; при v³0,8 растягивающие напряжения
не учитываются.
Величина наибольшей ординаты
эпюры растягивающих напряжений неармированной кладки должна удовлетворять
условию
st,max £ 0,8Rtb,u, (31)
где Rtb,u -
предел прочности кладки на растяжение при изгибе по перевязанному сечению,
равный Rtb,u = kRtb (k=2,25);
Rtb - расчетное сопротивление растяжению при изгибе.
Величины растягивающих
напряжений st,max в пределах высоты растянутой
зоны b при различных отношениях v = а/l можно определять по табл. 7.
Таблица 7
|
v =a/l |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
|
st,max |
0,383q |
0,295q |
0,216q |
0,157q |
0,116q |
0,089q |
|
b |
0,770а |
0,580a |
0,430а |
0,310a |
0,230a |
0,180a |
Если условие (31) не удовлетворяется, то горизонтальное
усилие st,max![]() (h – толщина стены) должно быть воспринято сетчатой
арматурой, уложенной в горизонтальных швах кладки в пределах высоты растянутой
зоны b.
Длина арматурных сеток должна обеспечивать их достаточную анкеровку. Для этого
сетки с одной стороны заводятся в пределы всей площади смятия и на такую же
длину в противоположную сторону, при этом длина сеток должна ограничиваться
краем стены.
(h – толщина стены) должно быть воспринято сетчатой
арматурой, уложенной в горизонтальных швах кладки в пределах высоты растянутой
зоны b.
Длина арматурных сеток должна обеспечивать их достаточную анкеровку. Для этого
сетки с одной стороны заводятся в пределы всей площади смятия и на такую же
длину в противоположную сторону, при этом длина сеток должна ограничиваться
краем стены.
Примечание. При опирании балок и ферм на
стены и столбы, изгиб или смещение которых в направлении продольной оси балки
ограничены, расчет опор следует производить с учетом температурно-влажностных
деформаций этих балок и стен. Для этого расчета могут быть применены указания прил. 11. При необходимости горизонтальные
усилия должны быть восприняты арматурой.
4.24. Неразрезные распределительные устройства (например, железобетонные пояса) рассчитываются как балки на упругом основании.
Армирование железобетонных
распределительных устройств производится в соответствии со СНиП
2.03.01-84.
4.25. В случае сложных узлов
опирания (например, при опирании на стену или столб прогонов, балок и плит в
нескольких направлениях, в одном или близких уровнях), расчет которых может
быть выполнен лишь ориентировочно, должны применяться конструктивные
мероприятия, повышающие надежность опорного узла, приведенные в п. 4.14, или узел должен быть замоноличен.
4.26. При опирании ферм,
балок покрытий, подкрановых балок и т. п. на пилястры следует предусматривать
связь распределительных плит на опорном участке кладки с основной стеной по п.
[6.42].
Выполнение кладки,
расположенной над плитами, следует предусматривать непосредственно после
установки плит. Предусматривать установку плит в борозды, оставляемые при
кладке стен, не допускается.
4.27.
Фиксирующая прокладка должна быть закреплена на поверхности плиты при помощи
выпущенных из нее анкеров. Внутренний край прокладки должен отстоять от края
опорной плиты не менее чем на 100 мм.
4.28. Под опорными участками
элементов, передающих местные нагрузки на кладку, следует предусматривать слой
раствора марки не ниже 50, толщиной не свыше 15 мм; установка этих элементов
или же распределительных плит на кладку „насухо" не допускается.
Кладка стен под опорами на
высоту не менее 10 рядов должна иметь цепную перевязку во всех рядах как в
продольном, так и в поперечном направлении, а кладка столбов или пилястр -
цепную или четырехрядную (системы Л.И. Онищика).
ИЗГИБ, ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СРЕЗ
4.29. Расчет изгибаемых и
центрально растянутых неармированных элементов, а также расчет неармированной
кладки на срез производятся по указаниям и формулам, приведенным в пп.
[4.18-4.20].
МНОГОСЛОЙНЫЕ СТЕНЫ
4.30. Проектирование
многослойных стен производится по пп. [4.21-4.29] и [6.30-6.31]. Многослойные
стены состоят из конструктивных, облицовочных и теплоизоляционных слоев,
соединенных жесткими или гибкими связями.
4.31. В двухслойных стенах
при жесткой связи слоев эксцентриситет продольной силы, направленный в сторону
теплоизоляционного слоя, не должен превышать 0,5у.
4.32. Трехслойные стены с
засылками или заполнением бетоном марки ниже 10 и двухслойные с утеплителем
марки 15 и ниже рассчитываются по сечению кладки без учета несущей способности
утеплителя.
4.33. Расчет и проектирование
стен с облицовками производятся по указаниям, приведенным в пп. [4.28 и 4.29]
и[6.32-6.34], а также в пп. 7.122-7.162.
УСТОЙЧИВОСТЬ ПОЛОЖЕНИЯ
4.34. При расчете стен в
процессе их возведения, а также сооружений, не имеющих верхней горизонтальной
опоры (например, промышленных дымовых труб, подпорных стен и т. п.), кроме
расчета на прочность и трещиностойкость необходима проверка на устойчивость
положения стены или сооружения. Это относится к сечениям, в которых не могут
быть восприняты растягивающие усилия, как, например, в уровне опирания
фундамента на грунт, стены - на гидроизоляционный слой и т. п.
Цель расчета - предупредить
опрокидывание конструкций при малой продольной и значительной поперечной силе.
В этом случае опрокидывание может произойти при обмятии или незначительном
выкрашивании одной лишь кромки сечения.
Устойчивость положения стены
обеспечивается при условии, если равнодействующая горизонтальных и вертикальных
сил находится в пределах сечения на достаточном расстоянии от его сжатого края,
т. е. при ограничении величины эксцентриситета.
Расчет производится по
формуле
![]() , (32)
, (32)
где М -
момент от расчетной поперечной нагрузки и внецентренного приложения нормальной
силы;
N - нормальная сила от
расчетного собственного веса элемента, вычисленного с учетом коэффициента
перегрузки 0,9;
m1 - коэффициент,
принимаемый для стен в стадии их возведения и свободно стоящих стен равным m1
=0,9, а для сооружений - по специальным указаниям;
у -
расстояние от центра тяжести элемента до края сечения в сторону
эксцентриситета.
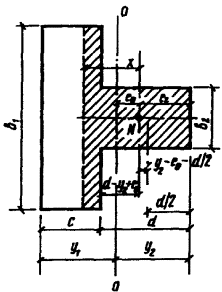
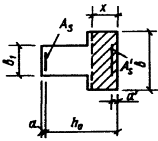
Пример 1. Расчет участка стены
таврового сечения на внецентренное сжатие (эксцентриситет в сторону ребра).
К тавровому
сечению простенка приложена расчетная продольная сила N = 850 кН (85 тс) и
расчетный момент, направленный в сторону ребра М = 102 кН×м (10,2 тс×м).
Размеры сечения приведены на черт. 6. Высота этажа Н =5 м. Кладка
выполнена из глиняного кирпича пластического прессования марки 100 на растворе
марки 50, расчетное сопротивление кладки R= 1,5МПа (15 кгс/см2).
Черт. 6. Поперечное тавровое сечение
Перекрытие сборное
железобетонное, заделанное на опорах в кладку стены, толщина перекрытия Hf=
0,22м.
Здание
жесткой конструктивной схемы (перекрытие является неподвижной горизонтальной
опорой стены).
Найти расчетную несущую
способность Ncc.
Эксцентриситет
![]() м.
м.
Расчет производим по
указаниям п. [4.7, формула (13)]:
N£mgj1RAcw.
Определяем геометрические
характеристики сечения.
Площадь сечения
А = 0,51×1,16+0,52×0,64= 0,924м2.
Определяем расстояние центра
тяжести сечения от края полки по графику прил. 5:
![]() ;
; ![]() ;
;
x = 0,43; z0 = 0,43×1,03 = 0,44 м.
Расстояние от центра тяжести
сечения до его края в сторону эксцентриситета
у =h - z0 = 1,03 - 0,44 = 0,59 м.
Момент инерции сечения
относительно его центра тяжести определяем по графику прил. 5:
I =
0,0605×1,16×1,033 =7,67×10-2 м4.
Радиус инерции сечения
 м
м
Так как i >
0,087 м, то согласно п. [4.7] принимается mg = 1.
Определяем значение
коэффициента продольного изгиба j для всего сечения.
Расчетная
высота простенка l0 при условиях, указанных в задании в
соответствии с п. [4.3, примеч. 1], принимается равной
l0 = 0,9H = 0,9
(5 - 0,22) = 4,3 м.
Гибкость простенка
определяется по формуле
![]() .
.
Упругая характеристика кладки
из глиняного кирпича пластического прессования, выполненной на растворе марки
50,
a = 1000 по табл. [15].
Коэффициент продольного
изгиба принимаем по табл.[18]
j=0,99.
Определяем площадь сжатой
части сечения.
Для определения размеров этой
площади применяем формулу
(2) прил. 6:
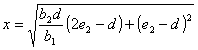 ,
,
где х -
расстояние от точки приложения силы до края полки сжатой части сечения.
Точка приложения силы
совпадает с центром тяжести сжатой части сечения
b1 = 1,16м; b2 = 0,64м; d= 0,52м;
е2 = у – е0
= 0,59 - 0,12 = 0,47 м;
 м.
м.
Высота сжатой части сечения
hс = е2 + х = 0,47 +
0,35 = 0,82 м.
Площадь сжатой части сечения
Ас = 0,64×0,32 + 0,30×0,26×2 = 0,681 м2.
Определяем момент инерции
сжатой части сечения относительно его центра тяжести по графику прил. 5:
![]() ;
;
![]() ; h=0,061;
; h=0,061;
Ic=hbh3=0,061×1,16×0,823=3,9×10-2
м4.
Радиус инерции сжатой части
сечения
 м
м
Коэффициент продольного
изгиба для сжатой части сечения при ![]() ; по табл. [18] jc=0,97
; по табл. [18] jc=0,97
![]() .
.
Так как радиус инерции
сечения i = 0,290 > 0,087 м, то коэффициент mg в формуле [13] принимаем
равным единице. Коэффициент w принимаем по табл. [19]:
![]() .
.
Расчетная несущая способность
простенка Ncc:
Ncc = mgj1RAcw = 0,98×1,5×0,681×1,1 103 = 1100 кН
> 850 кН (110 тc > 85 тc).
Расчетная продольная сила N
меньше расчетной несущей способности Ncc, следовательно, простенок
удовлетворяет требованиям прочности.
Относительный эксцентриситет
![]() ,
,
поэтому, согласно п. [4.8],
расчет по раскрытию трещин не производится.
Пример 2. Расчет участка стены
таврового сечения на внецентренное сжатие (эксцентриситет в сторону полки).
К тавровому сечению простенка
приложена продольная сила с эксцентриситетом e0=0,16 м в сторону полки. Размеры
простенка и все остальные данные см. на черт.
7.
Черт. 7. Поперечное тавровое сечение
Найти расчетную несущую
способность Ncc.
Расчет производим по формуле [13] п. [4.7]:
N £ mgj1RAcw.
Следующие
величины, не зависящие от эксцентриситета, вычисленные в примере 1, остаются без изменений:
z0 = 0,44м; a
= 1000; l0 = 4,30м;
mg = 1; j
= 0,99; R = 1,5 МПа (15 кгс/см2);
А = 0,924 м2; I = 7,67
10-2 м4.
Расстояние от центра тяжести
сечения до края сечения в сторону эксцентриситета
у = z0 = 0,44м.
Нормальная сила приложена на
расстоянии
e1 = z0 – е0 = 0,44-0,16
= 0,28м
от наружного края полки
сечения.
Определяем площадь сжатой
части сечения.
Для определения размеров этой
площади применяем формулу
(1) прил.6:
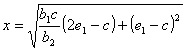 ,
,
где х - расстояние от точки
приложения силы до края ребра расчетной части сечения;
b1 = 1,16м; b2 = 0,64м; с= 0,51м; e1 = 0,28 м;
 м
м
Размеры расчетной сжатой
части сечения показаны на черт. 7.
Площадь сжатой части сечения
Ас = 1,16×0,51 + 0,09×0,64 = 0,649 м2.
Определяем момент инерции
сжатой зоны сечения относительно его центра тяжести по графику прил. 5:
![]() ;
;
![]() ; h=0,060;
; h=0,060;
Ic=hbh3;
Ic=0,060×1,16×0,603=1,5.10-2
м4
Радиус инерции сжатой части
сечения
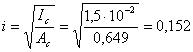 м.
м.
Коэффициент продольного
изгиба для сжатой части сечения при гибкости
![]() .
.
Принимаем по табл. [18] jс =
0,92 и определяем
![]() .
.
Коэффициент w
принимаем по табл. [19].
Так как 2у = 2×0,44 = 0,88 < h = 1,03, то коэффициент w
равен
![]() .
.
Расчетная несущая способность
сечения определяется по формуле [ 13]:
Nсс = mgj1RAcw = = 0,96×1,5×103×0,649×1,15 = 1080 кН > 850 кН
(108 тс > 85 тс).
Расчетная продольная сила N
меньше расчетной несущей способности Nсс следовательно, простенок
удовлетворяет требованиям прочности.
Относительный эксцентриситет
![]() .
.
Поэтому согласно п. [4.8]
расчет по раскрытию трещин не производится.
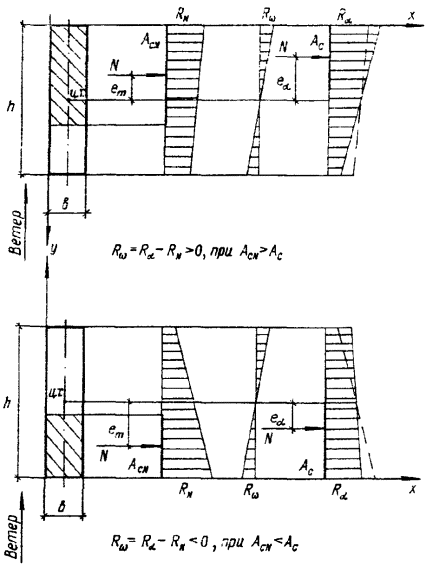
Пример 3. Расчет участка стены
таврового сечения по несущей способности и по раскрытию трещин.
К тавровому сечению простенка
приложена продольная сила с эксцентриситетом е0=0,45 м в сторону
ребра.
Размеры простенка и все
остальные данные см. на черт.8.
Найти расчетную несущую
способность Nсс. Следующие величины, не зависящие от
эксцентриситета, вычисленные в примере 1,
остаются без изменения:
z0 = 0,44м; a
= 1000; l0 = 4,30м;
mg = 1; j
= 0,99; R = 1,5 МПа (15 кгс/см2);
А = 0,924 м2; I = 7,67 10-2 м4.
Черт. 8. Поперечное тавровое сечение
Расстояние от центра тяжести
до края сечения в сторону эксцентриситета
у = h – z0 = 1,03 -0,44 = 0,59 м;
![]() ,
,
следовательно, простенок должен быть рассчитан не только по несущей способности, но и по раскрытию трещин в растянутой зоне сечения.
А. Вычисление Nсс по несущей способности.
Расчет производим по формуле
[13]:
Nсс = mgj1RAcw.
Расстояние s от
точки приложения силы до края ребра сечения равно
s = у – е0 = 0,59 - 0,45 = 0,14 м < ![]() ,
,
т. е. меньше половины высоты
ребра. Поэтому сжатая часть сечения прямоугольная и высота ее определяется по
формуле
hc = 2s = 2×0,14
= 0,28 м.
Расчетная сжатая часть
сечения показана на черт.8:
Ас = 0,28×0,64 = 0,179м2.
Коэффициент продольного
изгиба для сжатой части сечения при гибкости
![]()
по табл. [18] jc = 0,76:
![]() .
.
Коэффициент w
принимаем по табл. [19]:
![]() .
.
Расчетная несущая способность
простенка
Ncc = 0,88×1,5×103×0,179×1,38 = 326 кН (32,6 тc).
Б. Определение Ncc no раскрытию трещин в
растянутой зоне сечения производим по формуле [33] п. [5.3]:
 .
.
Согласно табл. [24] при
предполагаемом сроке службы конструкции 50 лет vr = 2,0.
По табл. [10] принимаем Rtb = 0,12 МПа и определяем
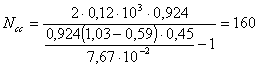 кН (16 тс).
кН (16 тс).
Таким образом, предельная
нагрузка на простенок определяется в данном случае расчетом по раскрытию трещин
в растянутой зоне сечения, а не расчетом по несущей способности.
Пример 4. Расчет несущей способности
участка несущей стены здания с жесткой конструктивной схемой.
К участку стены
прямоугольного сечения приложена расчетная продольная сила N = 165 кН (16,5
тс), от длительных нагрузок Ng = 150кН (15 тс),
кратковременных Nst = 15 кН (1,5 тc). Размер сечения 0,24´1,00м, высота этажа 3 м, нижние и верхние опоры стены - шарнирные,
неподвижные. Стена запроектирована из газобетонных блоков двухрядной разрезки,
смонтированных на растворе проектной марки М50; газобетон вида А плотностью 8
кН/м3 (800 кгс/м3) проектной марки по прочности М50.
Расчетная установившаяся влажность газобетона W = 10 % (по массе).
Требуется проверить несущую
способность элемента стены в середине высоты этажа при возведении здания в
летних условиях.
В соответствии с п. [4.9] для
несущих стен толщиной 0,24 м следует учитывать случайный эксцентриситет еv =
0,02 м. Следовательно, продольная сила будет действовать с эксцентриситетом e0 = e0g =
еv = 0,02 м. Расчет производим по формуле [13]:
N£ mgj1RAcw.
Находим геометрические
характеристики сечения. Площадь сечения элемента
А = 0,24×1,0 = 0,24м2.
Площадь сжатой части сечения
по формуле [14]:
![]() м2.
м2.
Расстояние от центра тяжести
сечения до края сечения в сторону эксцентриситета
![]() м.
м.
Расчетное сопротивление
сжатию кладки R по табл. [4] с учетом коэффициента условий работы gс =
0,8, см. п. [3.11], равно
R = 1,5×1,1×0,8 = 1,32 МПа (13,2 кгс/см2).
Расчетная длина элемента
согласно черт. [4, а], п. [4.3] равна
l0 = H = 3 м.
Гибкость элемента равна
![]() .
.
Упругая характеристика кладки
a, принимаемая по табл. [15], равна
a = 750.
Коэффициент продольного
изгиба определяем по табл. [18]:
j
= 0,775.
Гибкость сжатой части сечения
![]() .
.
Коэффициент продольного
изгиба сжатой части сечения по табл. [18]:
jc = 0,705.
По формуле [15] определяем
коэффициент j1:
![]() .
.
Коэффициент w
для ячеистого бетона принимается по табл. [19] равным 1,0.
Коэффициент h
при lhc = 15 по табл. [20] принимаем
равным 0,115.
Коэффициент mg по формуле [16] равен
 .
.
Расчетная несущая способность
участка стены Ncc равна
Nсс = mgj1RAcw = 0,885×0,74×1,32×103×0,2×1
= 172,9 кН
(17,29 тc).
Расчетная
продольная сила N меньше Nсс:
N = 165 кН < Ncc = 172,9 кН.
Следовательно, стена
удовлетворяет требованиям по прочности. Эксцентриситет е0=0,02 м,
что меньше 0,7 у = 0,7×0,12 = 0,084 м, поэтому в
соответствии с п. [4.8] не следует производить расчет по раскрытию трещин.
Пример 5. Расчет участка внутренней
несущей стены здания с жесткой конструктивной схемой на внецентренное сжатие.
К участку стены
прямоугольного сечения приложена расчетная продольная сила N=200 кН
(20 тc) от длительных нагрузок Ng = 180 кН (18 тc),
кратковременных Nst = 2кН (2 тc) и расчетный момент М = 3,9
кН×м (0,39 тc×м). Размер сечения 0,24´1,00 м, высота этажа H = 3 м, нижние и верхние
опоры стены - шарнирные неподвижные. Стена запроектирована из газобетонных
блоков двухрядной разрезки, смонтированных на растворе проектной марки М50; газобетон
вида А плотностью 10 кН/м (1000 кгс/м3), проектной марки по
прочности М100. Расчетная установившаяся влажность газобетона W = 10%
(по массе).
Требуется проверить несущую
способность элемента стены в середине высоты этажа при возведении здания в летних
условиях. Эксцентриситет от расчетной продольной силы равен
e0 = M/N = 3,9:200 = 0,0195 м.
Случайный эксцентриситет в
соответствии с п. [4.9] для несущих стен толщиной 0,24 м равен ev = 0,02 м. Эксцентриситет от действия длительных нагрузок e0g1 =
M/Ng=3,9:180 = 0,0217 м.
Расчетный эксцентриситет
принимаем равным:
от расчетной продольной силы
с учетом случайного эксцентриситета
e0=e01+ev = 0,0195+0,02 = 0,0395м @ 0,04м;
от действия длительных
нагрузок с учетом случайного эксцентриситета
e0g=e0g1+ev = 0,0217 + 0,02 = 0,0417 м @ 0,042 м.
Расчет производим по формуле
[13]
N£ mgj1RAcw.
Находим геометрические
характеристики сечения. Площадь сечения элемента
А = 0,24×1,0 = 0,24м2.
Площадь сжатой части сечения
по формуле [14]
![]() м2.
м2.
Расстояние от центра тяжести
сечения до края сечения в сторону эксцентриситета
![]() м.
м.
Расчетное сопротивление
сжатию кладки R по табл. [4] с учетом коэффициента условий работы gс =
0,8 п. [3.11] равно
R = 2,7×1,1×0,8 = 2,376 МПа (23,76 кгс/см2).
Расчетная длина элемента l0 согласно черт. [4, a], п. [4.3]
l0 = H = 3 м.
Гибкость элемента по формуле
[12]
![]() .
.
Упругая характеристика a
по табл. [15] равна 750.
Гибкость сжатой части сечения
lhc равна
![]() .
.
Коэффициент продольного
изгиба сжатой части сечения jc
по табл. [18] равен 0,611.
По формуле [15] коэффициент ![]() .
.
Коэффициент w
для ячеистого бетона принимаем по табл. [19] равным 1,0.
Коэффициент h
при lhc = 18,75 по табл. [20]
принимаем равным 0,209.
Коэффициент mg, по формуле [16] равен
 .
.
Расчетная несущая способность
элемента стены
Ncc = mgj1RAcw = 0,772×0,693×2,376×103×0,16×1 = 203,4 кН (20,34 тc).
Расчетная продольная сила N
меньше расчетной несущей способности Ncc:
N = 200 кН < Ncc = 203,4 кН.
Следовательно, стена
удовлетворяет требованиям по прочности. Относительный эксцентриситет e0/у = 0,04:0,12 = 0,33 <
0,7, поэтому в соответствии с п. [4.8] расчет по раскрытию трещин производить
не требуется.
Пример 6. Расчет кладки на смятие под
опорами свободно лежащей однопролетной стальной двутавровой балки чердачного
перекрытия.
Балка № 20 с моментом инерции
поперечного сечения I = 1840×10-8 м4
длиной 6,4 м с пролетом (в свету) 6 м, шириной полки b = 0,1 м и длинами опорных
концов a1 =
0,2 м с каждой стороны. Балка нагружена равномерно распределенной нагрузкой q = 5
кН/м (500 кгс/м), включая ее собственный вес. Балки чердачного перекрытия
опираются на кирпичные стены толщиной 0,51 м, выполненные из кирпича марки 100
на растворе марки 50. Расчетное сопротивление кладки 1,5 МПа. Расстояние между
балками 1,5 м. Опорная реакция балки Q = 15 кН (1,5 тc).
Расчет кладки на смятие под
опорами балки производим по п. [4.15].
Полезную длину опоры a0 определяем по формуле (13):
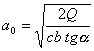 .
.
Коэффициент постели с
при смятии кладки под концом балки при затвердевшей кладке определяется по
формуле
![]() МН/м3 (1,5×105 тс/м3)
МН/м3 (1,5×105 тс/м3)
При равномерно распределенной
нагрузке тангенс угла наклона оси балки в середине опорного конца определяется
по формуле
![]() ;
;
 м <0,2 м.
м <0,2 м.
Расчет кладки на смятие под
опорами балки производится по формуле [17] п. [4.13]:
Nс £
ydRсAc.
Так как полезная длина опоры
балки a0
меньше ее полной длины a1, то эпюра распределения
напряжений принимается по треугольнику с коэффициентом полноты y=0,5; d=1,5-0,5y=1,25. По п. [4.14] расчетное
сопротивление кладки при смятии Rc=xR. Расчетная площадь сечения А принимается по п.
[4.16в]:
А = (0,1+0,51×2)0,125 = 0,14м2.
Площадь смятия Аc =
0,1×0,125 = 0,0125 м2.
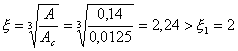 .
.
Расчетное сопротивление
кладки на смятие Rc = xR.
Rc = 1,5×2 = 3 МПа.
Расчетная несущая способность
затвердевшей кладки при смятии
Nсc £
ydRсAc=0,5×1,25×3×0,0125×103=23,4>Q=15 кН (2,34 тс>1,5 тс).
Расчетная нагрузка на стену
при смятии меньше расчетной несущей способности кладки, следовательно,
затвердевшая кладка под опорой балки удовлетворяет требования прочности.
Определяем расчетную несущую
способность свежей кладки при смятии.
Коэффициент постели с1
для свежей кладки при прочности раствора 0,2 МПа и расчетном сопротивлении
кладки 0,8 МПа определяется по формуле
![]() мН/м3
(0,56×105 тс/м3);
мН/м3
(0,56×105 тс/м3);
tg a=0,0128;
 м > 0,2 м.
м > 0,2 м.
Краевые напряжения при эпюре
в виде трапеции определяются по формулам:
![]() МПа;
МПа;
![]() МПа
МПа
![]() МПа
МПа
Коэффициент полноты эпюры
давления при эпюре напряжений под опорой балки в виде трапеции определяется по
формуле
 ;
;
d =
1,5-0,5×0,51 = 1,245.
Расчетная площадь сечения А =
(0,1+0,51×2)0,2= 0,224м2.
Площадь смятия Aс = 0,1×0,2 = 0,02 м2.
Коэффициент определяем по
формуле [19]:
 ;
;
Rc = 0,8×2 = 1,6 МПа.
Расчетная несущая способность
свежей кладки при смятии
Ncc = 0,51×1,245×1,6×103×0,02 = 20,3 кН > Q = 15 кН (2,03 тс > 1,5
тс).
Расчетная нагрузка на стену
при смятии меньше расчетной несущей способности кладки, следовательно, свежая
кладка под опорой балки также удовлетворяет требованиям прочности.
Пример 7. Расчет на смятие кладки
под опорным участком балки покрытия.
Рассчитать и
сконструировать опоры для двускатных балок покрытия над одноэтажным
промышленным зданием пролетом 15 м. Балки опираются на наружные стены с
пилястрами, шаг - 6м. Стены толщиной 0,38 м возводятся из кирпича марки 75 на
растворе марки 50, сечение пилястр 0,39´0,51 м, см. черт.
9 и 10. Учитывая, что монтаж
покрытия может быть произведен через 7-10 сут после возведения кладки и при
температуре, равной 10°С, принимаем прочность раствора с коэффициентом 0,5 (см. табл. 1), т. е. марки 25.
Черт. 9. Схема узла опирания
балки на стену под опорной
пятой в направления оси балки
Черт. 10. Распределение напряжений в кладке под опорной
плитой
в поперечном направлении
Вертикальная расчетная
нагрузка на опору N = 250 кН (25 тc). Балки опираются на кладку
через железобетонные распределительные плиты, расположенные по всему сечению
пилястр и на части сечения наружной стены.
Принимаем предварительные
размеры опорной плиты: ширину, равную ширине пилястры, длину 0,64 м и высоту
0,22 м. Армирование плиты производим в соответствии с требованиями п. 4.14.
Балка на опорную плиту
опирается через фиксирующую прокладку, размеры которой определяются из условия
местного смятия бетона плиты.
Наиболее благоприятное
распределение напряжений под опорной плитой будет при размещении фиксирующей
прокладки по центральным осям опорной плиты. В этом случае коэффициент
неравномерности распределения напряжений под опорной плитой определяется в
основном жесткостью этой плиты.
Напряжения вдоль оси опорной
плиты, перпендикулярной оси стены, определяем по формулам табл. 6 поз. 2 (см. черт. 9):
а = 0,32м; d = 0,51
м.
Модуль упругости опорной
плиты
Е = 0,85Eb = 0,85×265×102 = 225×102 МПа.
Момент инерции
распределительной плиты
![]() м4.
м4.
Модуль упругости кладки
Е = 0,5 Е0 = 0,5 aRu = 0,5×1000×2,2 = 1100 МПа.
Высота распределительной
плиты
 м.
м.
По табл. 6 поз. 2 принимаем
 МПа (8,8 кгс/см2);
МПа (8,8 кгс/см2);
 МПа (6,50 кгс/см2).
МПа (6,50 кгс/см2).
Определяем коэффициент
полноты эпюры давления y1, учитывая, что объем эпюры
давления равен N
![]() .
.
Напряжения вдоль оси опорной
плиты, параллельной оси стены, определяем по табл. 6, поз. 8 (см. черт. 10):
![]() кН/м;
кН/м;
b=0,20 м;
d1=0,64
м; а=0,255 м.
По формуле (26) находим
 м;
м;
![]() ;
;
![]() МПа (8,30 кгс/см2);
МПа (8,30 кгс/см2);
![]() МПа (7,03 кгс/см2);
МПа (7,03 кгс/см2);
s1=0,703 МПа<R=1,1 МПа (11 кгс/см2)
![]() ;
;
y=y1y2=0,87×0,92=0,80.
Расчетную несущую способность
опоры определяем в соответствии с формулой [17]:
Nсc=ydRсAc;
d=1,5-0,5y=1,5-0,5×0,80=1,1;
yd=0,80×1,1=0,88;
Rc=xR=1×1,1 МПа;
Ac = 0,51×0,64=0,326 м2;
Ncc=0,88×1,1×0,326×103=316 кН>N=250
кН(31,6 тс>25 тc).
Кирпичную кладку под опорной
плитой в соответствия с пп. 4.14 и 4.23 армировать не требуется, так как N<0,8Nc и v>0,8.
5. РАСЧЕТ И КОНСТРУИРОВАНИЕ АРМИРОВАННЫХ,
КОМПЛЕКСНЫХ И УСИЛЕННЫХ ОБОЙМАМИ
КАМЕННЫХ КОНСТРУКЦИЙ
ОБЩИЕ УКАЗАНИЯ
5.1. В строительстве
применяются следующие виды армирования и усиления каменных конструкций:
поперечное (сетчатое с
расположением арматурных сеток в горизонтальных швах кладки);
продольное с расположением
арматуры снаружи под слоем цементного раствора или в бороздах,
армирование (усиление)
посредством включения в кладку железобетона (комплексные конструкции);
усиление посредством
включения элемента в железобетонную или металлическую обойму из уголков.
Армирование каменных
конструкций значительно повышает их несущую способность и монолитность,
обеспечивает совместную работу отдельных частей зданий, а также является
основным способом увеличения сейсмостойкости каменных конструкции и здания в
целом.
5.2. Для армокаменных элементов
применяется кирпич всех видов, керамические и силикатные пустотелые камни,
природные и искусственные камни, удовлетворяющие требованиям государственных
стандартов на соответствующие материалы.
Марка кирпича, применяемая
для армокаменных конструкций, должна быть не менее 75, камня - не менее 35 и
раствора - не менее 50.
5.3. Расчетные сопротивления
кладки для элементов с сетчатым армированием (пп. [4.30 и 4.31]) принимаются по
п. [3.4]. При кладке из камней марки 35 и выше (п. [3.4]) эффективность
сетчатого армирования снижается, и расчетное сопротивление кладки принимается Rsk£1,5R.
5.4. Расчетные сопротивления
сжатию бетона принимаются по СНиП 2.03.01-84.
5.5. Для армирования каменных
конструкций следует применять:
для сетчатого армирования -
сталь горячекатаную круглую гладкую класса A-I и Вр-I;
для продольного армирования,
анкеров и связей - арматуру классов A-I, A-II и Вр-I с
учетом коэффициентов условий работы, приведенных в п. [3.19];
для конструкций, усиленных стальными обоймами, допускается применять полосовую, листовую и фасонную сталь, удовлетворяющую требованиям, установленным для подобных элементов стальных и железобетонных конструкций соответствующими нормативными документами.
При соответствующем
обосновании допускается также армирование стержнями из других видов стали,
применяемых в железобетонных конструкциях.
5.6. Нормативные Rcn и расчетные Rs сопротивления арматуры принимаются по пп. [3.19 и
3.20] и СНиП 2.03.01-84.
Модули упругости и упругие
характеристики кладки с сетчатым и продольным армированием принимаются по п.
[3.20].
5.7. Марка раствора для
армокаменных и комплексных конструкций принимается не ниже 50. Защитный слой
цементного раствора для армокаменных конструкций с арматурой, расположенной
снаружи кладки, должен иметь толщину (от внешней грани рабочей арматуры) не
менее указанной в табл. 8.
Таблица 8
|
Армированные конструкции |
Защитный слой, мм, для
конструкций, расположенных |
||
|
в помещениях с нормальной
влажностью |
на открытом воздухе |
во влажных и мокрых
помещениях, а также в резервуарах, фундаментах и т. п. |
|
|
Балки и столбы |
20 |
25 |
30 |
|
Стены |
10 |
15 |
20 |
5.8. Процент армирования
стены горизонтальной арматурой, учитываемой в расчете, должен быть не ниже 0,05
для каждого направления. При армировании стен железобетонными поясами или
стойками процент армирования следует относить к площади сечения стены,
приходящейся на один железобетонный элемент.
Расстояние между
вертикальными и горизонтальными стержнями или между арматурными поясами и
стойками не должно превышать 8h, где h -
толщина стены. При армировании поясами или стойками расстояния между ними могут
быть увеличены при условии проверки расчетом прочности панели стены на участках
между ними.
5.9. Армирование стен должно
предусматриваться с соблюдением следующих правил:
горизонтальная арматура стен,
как правило, располагается в швах кладки;
при однозначной нагрузке
устанавливается одиночная продольная арматура с растянутой стороны стены, а при
знакопеременной нагрузке - двойная (двусторонняя арматура);
вертикальная арматура,
конструктивная или работающая на растяжение, расположенная снаружи стены,
связывается хомутами не реже чем через 30 диаметров;
тонкие стены из кирпича „на
ребро" могут быть армированы вертикальными и горизонтальными стержнями в швах кладки с
размерами ячеек арматурной сетки 52´52 или 52´65 см;
концы горизонтальных и
вертикальных стержней рекомендуется заделывать в устойчивые прилегающие
конструкции (капитальные стены, колонны, обвязочные балки и т. п.) и
заанкеривать.
5.10. При продольном армировании стен (например, в армокаменных поясах) допускается применение стержней арматуры диаметром до 12 мм с утолщением шва до 25 мм.
ЭЛЕМЕНТЫ С СЕТЧАТЫМ ПОПЕРЕЧНЫМ
АРМИРОВАНИЕМ (СТОЛБЫ, ПРОСТЕНКИ,
ОТДЕЛЬНЫЕ УЧАСТКИ)
5.11. Расчет и
проектирование элементов с сетчатым армированием производятся по указаниям,
приведенным в пп. [4.30 и 4.31] и [6.75-6.77]. Наряду с квадратными применяются
также прямоугольные сетки (черт. 11).
Черт. 11. Сетчатое
армирование каменных конструкций
1 - арматурная сетка; 2 - выпуск арматурной сетки для
контроля ее укладки;
а - квадратная сетка; б - прямоугольная сетка
5.12. Не допускается применять
сетчатое армирование стен помещений с влажным и мокрым режимами.
5.13. При армировании кладки
сетками с прямоугольными ячейками (см. черт.
11, б) процент армирования кладки определяется по формуле
![]() . (33)
. (33)
5.14. Эффективность сетчатого
армирования кирпичной кладки при расположении сеток реже чем через 45 см
снижается. Такое армирование может применяться: как конструктивное с
расположением сеток по высоте элемента на расстоянии до 1 м. Сетки в этом
случае в расчет не вводятся, но они препятствуют расслоению кладки и внезапному
ее разрушению.
5.15. Для подбора размеров
ячеек сеток и расстояния между сетками по высоте элемента при заданном проценте
армирования (пли расположении их в каждом шве кладки при высоте ряда 7,7; 10 и
15 см) рекомендуется пользоваться табл. 9.
|
Размер
ячейки с, см |
Диаметр
арматуры, мм |
|||
|
3 |
4 |
5 |
6 |
|
|
%
армирования сетками |
||||
|
s = 7,7 см (обычный кирпич h = 65 мм) |
||||
|
3´3 |
0,61 |
1,09 |
1,7 |
2,45 |
|
3,5´3,5 |
0,53 |
0,93 |
1,45 |
2,15 |
|
4´4 |
0,46 |
0,82 |
1,27 |
1,84 |
|
4,5´4,5 |
0,41 |
0,73 |
1,13 |
1,64 |
|
5´5 |
0,37 |
0,66 |
1,02 |
1,47 |
|
5,5´5,5 |
0,34 |
0,6 |
0,92 |
1,34 |
|
6´6 |
0,31 |
0,55 |
0,85 |
1,23 |
|
6,5´6,5 |
0,28 |
0,5 |
0,78 |
1,13 |
|
7´7 |
0,26 |
0,47 |
0,73 |
1,05 |
|
7,5´7,5 |
0,25 |
0,44 |
0,68 |
0,98 |
|
8´8 |
0,23 |
0,41 |
0,64 |
0,92 |
|
8,5´8,5 |
0,22 |
0,39 |
0,6 |
0,87 |
|
9´9 |
0,21 |
0,36 |
0,57 |
0,82 |
|
9,5´9,5 |
0,19 |
0,34 |
0,54 |
0,77 |
|
10´10 |
0,18 |
0,33 |
0,51 |
0,74 |
|
s = 10 см (утолщенный кирпич h = 88 мм) |
||||
|
3´3 |
0,47 |
0,84 |
131 |
1.89 |
|
3,5´3,5 |
0.41 |
0.72 |
1J2 |
Ui2 . |
|
4´4 |
036 |
0,63 |
0,98 |
1,42 |
|
4,5´4,5 |
032 |
0,56 |
0.87 |
1.26 |
|
5´5 |
0,28 |
0.5 |
0.78 |
143 |
|
5,5´5,5 |
0,26 |
0,46 |
0.71 |
1,03 |
|
6´6 |
04 |
0.42 |
0.65 |
0,94 |
|
6,5´6,5 |
02 |
039 |
0 |
07 |
|
7´7 |
0.2 |
036 |
036 |
031 |
|
7,5´7,5 |
0,19 |
034 |
032 |
0,76 |
|
8´8 |
ОД8 |
032 |
0.49 |
0,71 |
|
8,5´8,5 |
0.17 |
03 |
0,46 |
067 |
|
9´9 |
0.16 |
0,28 |
0.44 |
0,63 |
|
9,5´9,5 |
0.15 |
0.27 |
0.42 |
0,6 |
|
10´10 |
OJ4 |
0,25 |
039 |
037 |
|
s = 15 см (камень h=138 мм) |
||||
|
3´3 |
0,32 |
0,56 |
0,87 |
1,26 |
|
3,5´3,5 |
0,27 |
0,48 |
0,75 |
1,08 |
|
4´4 |
0,24 |
0,42 |
0,65 |
0,94 |
|
4,5´4,5 |
0,21 |
0,37 |
0,38 |
0,84 |
|
5´5 |
0,19 |
0,34 |
0,52 |
0,75 |
|
5,5´5,5 |
0,17 |
0,31 |
0,48 |
0,69 |
|
6´6 |
0,16 |
0,28 |
0,44 |
0,63 |
|
6,5´6,5 |
0,15 |
0,26 |
0,4 |
0,58 |
|
7´7 |
0,14 |
0,24 |
0,37 |
0,54 |
|
7,5´7,5 |
0,13 |
0,22 |
0,35 |
0,5 |
|
8´8 |
0,12 |
0,21 |
0,33 |
0,47 |
|
8,5´8,5 |
0,11 |
0,2 |
0,31 |
0,44 |
|
9´9 |
0,1 |
0,19 |
0,29 |
0,42 |
|
9,5´9,5 |
0,1 |
0,18 |
0,28 |
0,4 |
|
10´10 |
0,09 |
0,17 |
0,26 |
0,38 |
Примечание. При расположении сеток не в
каждом шве кладки, а через 2-5 рядов, приведенный в таблице процент армирования
уменьшается пропорционально числу рядов.
ЭЛЕМЕНТЫ С ПРОДОЛЬНЫМ АРМИРОВАНИЕМ
5.16. Продольное армирование
каменных конструкций может применяться в отдельных конструктивных элементах
(стенах, столбах, перемычках, подпорных стенах и т. п.) для восприятия
растягивающих усилий во внецентренно сжатых (при больших эксцентриситетах) и
изгибаемых элементах, а также для повышения прочности и устойчивости тонких
стен при ![]() .
.
Продольное армирование
каменных конструкций применяют с целью повышения сопротивляемости кладки
растягивающим усилиям и обеспечения монолитности и устойчивости отдельных
частей и всего сооружения в целом.
При продольном армировании каменных
конструкций арматура укладывается снаружи под слоем цементного раствора или в
штрабе кладки с заполнением штрабы раствором (черт. 12).
Черт. 12. Продольное
армирование кирпичных конструкций (столбов, стен и др.)
а - наружное расположение
арматуры; б - расположение арматуры в штрабе кладки; 1 - поперечные хомуты; 2 -
продольная арматура
5.17. Количество арматуры,
учитываемой при расчете столбов и простенков, должно составлять не менее, %:
для сжатой продольной
арматуры ........... 0,1
для растянутой продольной
арматуры .......... 0,05
5.18. При расчете элементов,
работающих на центральное и внецентренное сжатие, учитывается неполное
использование прочности кладки при сжатии, работающей совместно с арматурой,
введением коэффициента условий работы кладки 0,85, на который умножается
расчетное сопротивление кладки, а также неполное использование работы сжатой
продольной арматуры, расчетное сопротивление которой определяется по п. [3.19].
При расчете элементов, работающих
на внецентренное сжатие, расчетное сопротивление кладки принимается равным wR (w - коэффициент, принимаемый по п. [4.7]).
5.19. В изгибаемых элементах
применение сжатой арматуры, учитываемой в расчете, допускается только в
исключительных случаях, например, при ограниченной высоте сечения, при действии
знакопеременных моментов и т.п.
5.20. В элементах с продольной арматурой, расположенной снаружи кладки, площадь сечения защитных (растворных) слоев в расчете не учитывается.
5.21. Расчет армированных
каменных конструкций с продольной арматурой по трещинам производится по
указаниям разд. 6.
5.22. Расчет элементов с
продольной арматурой при центральном сжатии (черт. 13, a)
производится по формулам:
N£j(0,85mgRA+RscAs¢); (34)
![]() ; (35)
; (35)
![]() , (36)
, (36)
где N - продольная расчетная сила;
j - коэффициент продольного изгиба,
принимаемый по п. [4.2];
mg - коэффициент, учитывающий влияние длительной нагрузки, см. п. [4.1];
R -
расчетное сопротивление кладки;
А - площадь сечения кладки;
Rsc - расчетное сопротивление продольной сжатой арматуры, принимаемое по
п. [3.19];
Аs¢ - площадь сечения
продольной арматуры.
Упругая характеристика
кладки a с продольным армированием
принимается по п. [3.21] как для неармированной кладки, п. [3.20].
5.23. При внецентренном
сжатии различают случаи внецентренно сжатых элементов (черт. 13, б, в):
случай 1, когда соблюдается условие:
при любой форме сечения
Sc<0,8S0; (37)
при прямоугольной форме
сечения
х<0,55h0; (38)
случай 2, когда соблюдается условие:
при любой форме сечения
Sc³0,8S0; (39)
при прямоугольной форме
сечения
х³0,55h0; (40)
Черт. 13. Внецентренное сжатие армированной кладки
a - центральное сжатие; б - случай 1Sс<0,8S0; в - случай 2Sс>0,8S0
В формулах (34)-(40):
Sc - статический момент сжатой зоны сечения кладки относительно центра
тяжести растянутой или менее сжатой арматуры Аs;
S0 - статический момент всего сечении кладки относительно центра тяжести растянутой Аs или менее сжатой арматуры;
х - высота сжатой зоны
сечения, определяемая по прил.
7, табл. 1.
Статический момент S0 при любой форме сечения
определяется по формуле
S0=A(h0-y), (41)
где А - площадь сечения
кладки;
h0 - рабочая высота сечения h0 =h - а;
h -
высота всего сечения;
a -
толщина защитного слоя со стороны арматуры Аs;
у - расстояние от центра
тяжести всего сечения до края наиболее сжатой грани.
При прямоугольной форме
сечения
![]() , (42)
, (42)
где b - ширина прямоугольного
сечения.
Статический момент Sc зависит от формы и размеров сечения, положения нейтральной оси и
защитного слоя. Формулы для наиболее часто встречающихся случаев при
определении Sc приведены в табл. 7 прил. 7. В табл. 2, 3 и 4 этого
приложения приведены формулы для расчета внецентренно сжатых элементов с
продольной арматурой, а также пояснения к таблицам.
5.24. Расчет армированных
изгибаемых элементов прямоугольного сечения со стержневой арматурой производится
по формулам:
а) при двойной арматуре
![]() , (43)
, (43)
при этом положение
нейтральной оси определяется по формуле
![]() ; (44)
; (44)
б) при одиночной арматуре
![]() , (45)
, (45)
при этом положение нейтральной оси определяется по
формуле
RsAs=1,25Rbx. (46)
Высота сжатой зоны кладки
должна во всех случаях удовлетворять условиям:
x£0,55h0 и x³2a¢. (47)
5.25. Расчет изгибаемых
элементов на поперечную силу производится по формуле
Q£Rtwbz. (48)
При прямоугольном сечении
![]() . (49)
. (49)
Примечание.
Если прочность
кладки при расчете на поперечную силу окажется недостаточной, необходима
установка хомутов или устройство отгибов в арматуре, расчет которых
производится в соответствии с указаниями СНиП 2.03.01-84.
5.26. Расчет элементов
продольно армированной кладки при центральном растяжении производится по
формуле
N£RsAs. (50)
КОМПЛЕКСНЫЕ ЭЛЕМЕНТЫ
(ЭЛЕМЕНТЫ ИЗ КАМЕННОЙ КЛАДКИ,
УСИЛЕННЫЕ ЖЕЛЕЗОБЕТОНОМ)
5.27. Комплексными
называются элементы каменной кладки с включением в них железобетона,
работающего совместно с кладкой. При этом железобетон рекомендуется располагать
с внешней стороны кладки (черт. 14),
что позволяет проверить плотность уложенного бетона и является более
рациональным при внецентренном сжатии, продольном изгибе и изгибе конструкции.
Черт. 14. Схемы сечений комплексных элементов
а - одностороннее
расположение железобетона, б - расположение железобетона в штрабе
5.28. Комплексные
конструкции применяются в тех же случаях, что и кладка с продольным
армированием, а также когда требуется значительно увеличить несущую способность
сильно нагруженных элементов при центральном или внецентренном сжатии.
Применение в этом случае комплексных конструкций позволяет уменьшить размеры
сечений элементов.
Для комплексных конструкций
применяются материалы, указанные в п. 5.2 и
бетон марки не выше 150.
5.29. При конструировании
комплексных элементов площадь сечения всей продольной арматуры должна
составлять не более 1,5 % площади сечения бетона.
5.30. При расчете
комплексных элементов на центральное сжатие следует соблюдать следующее условие
![]() , (51)
, (51)
где N- продольная сила;
mg - коэффициент, учитывающий влияние длительности нагрузки, см. п.
[4.1];
R -
расчетное сопротивление кладки;
А - площадь сечения кладки;
Rb и Rsc - расчетные сопротивления
бетона и арматуры при центральном сжатии, принимаемые по СНиП
2.03.01-84;
Ab - площадь сечения бетона;
![]() - площадь сечения
арматуры;
- площадь сечения
арматуры;
jcs - коэффициент продольного
изгиба комплексной конструкции, принимаемый по п. [4.2] при упругой
характеристике кладки
![]() , (52)
, (52)
Приведенный модуль упругости
комплексных элементов и приведенное временное сопротивление комплексного
сечения определяются по формулам:
![]() ; (53)
; (53)
![]() . (54)
. (54)
В формулах (53) и (54):
E0k,
Eb - начальные модули упругости кладки и бетона,
определяемые для кладки по п. [3.20], для бетона - по СНиП
2.03.01-84;
Ik, Ib - моменты инерции сечения кладки и бетона;
Ru= 2R - временное сопротивление
(средний предел прочности) сжатию кладки;
Rub - нормативная призменная прочность бетона при сжатии, принимаемая по СНиП
2.03.01-84.
5.31. Различают случаи
внецентренно сжатых комплексных элементов (аналогично каменным элементам с
продольным армированием):
а) случай 1, когда
соблюдается условие
Sc³0,8S0; (55)
б) случай 2, когда
соблюдается условие
Sc<0,8S0; (56)
В случае 1 расчет производится
по формуле
![]() . (57)
. (57)
При этом, если сила N
приложена между центрами тяжести арматуры Аs и ![]() , то должно быть удовлетворено дополнительное условие:
, то должно быть удовлетворено дополнительное условие:
При одиночной арматуре (![]() =0) расчет производится по формуле
=0) расчет производится по формуле
В формулах (55) - (59):
![]() - статический момент
площади комплексного сечения (приведенного к кладке) относительно
центра тяжести растянутой или менее сжатой арматуры Аs;
- статический момент
площади комплексного сечения (приведенного к кладке) относительно
центра тяжести растянутой или менее сжатой арматуры Аs;
![]() - статический момент площади сжатой зоны
комплексного сечения относительно центра тяжести арматуры Аs,
- статический момент площади сжатой зоны
комплексного сечения относительно центра тяжести арматуры Аs,
Skc и Sbc - статические моменты площадей сжатой части
сечения кладки и бетона относительно центра тяжести арматуры Аs;
Sk, Sb и Ss - статические моменты
площадей сечения кладки, бетона и арматуры ![]() относительно центра
тяжести арматуры Аs;
относительно центра
тяжести арматуры Аs;
Sk1,
Sb1 и ![]() - статические моменты
площадей сечения кладки, бетона и арматуры Аs относительно центра тяжести
арматуры
- статические моменты
площадей сечения кладки, бетона и арматуры Аs относительно центра тяжести
арматуры ![]() ;
;
е и е¢ - расстояния от точки
приложения силы N до центра тяжести арматуры Аs и ![]() .
.
Если центры тяжести арматуры
Аs и ![]() находятся на
расстоянии свыше 5 см от граней сечения, то в формулах (58) и (59) статические моменты и эксцентриситеты е и е¢ определяются относительно
грани сечения.
находятся на
расстоянии свыше 5 см от граней сечения, то в формулах (58) и (59) статические моменты и эксцентриситеты е и е¢ определяются относительно
грани сечения.
При внецентренно сжатых
элементах комплексных конструкций с большими эксцентриситетами (с расположением
бетона с внешней стороны кладки), при которых соблюдается условие Sc<0,8S0 , расчет производится по формуле
Положение нейтральной оси в
этом случае определяется из уравнения
В формуле
(61) знак „плюс" принимается, если сила N приложена за пределами
расстояния между центрами тяжести арматуры Аs и ![]() ; знак „минус" - если сила N приложена между центрами
тяжести арматуры Аs
и
; знак „минус" - если сила N приложена между центрами
тяжести арматуры Аs
и ![]() .
.
При одиночной арматуре (![]() = 0) расчет производится по формуле
= 0) расчет производится по формуле
![]() . (62)
. (62)
и положение нейтральной оси
определяется из уравнения
В формулах (60) - (63):
Acs - площадь сжатой зоны кладки;
Abc - площадь сжатой зоны бетона;
Scs,N - статический момент сжатой зоны кладки
относительно точки приложения силы;
Sbs,N - статический момент сжатой зоны бетона
относительно точки приложения силы.
5.32. Расчет изгибаемых
элементов комплексных конструкций производится по формуле
M£RScs+RbSbc+RsSs; (64)
положение нейтральной оси
определяется из уравнения
![]() . (65)
. (65)
Высота сжатой зоны
комплексного сечения должна во всех случаях удовлетворять условиям:
Sc<0,8S0 и z£h0-a¢. (66)
При этом значения S0 и Sc, а также Scs и Sbc принимаются такими же, как при внецентренном
сжатии, а плечо внутренней пары сил z принимается равным
расстоянию от точки приложения равнодействующей усилий RAcs и RbAbs до центра тяжести арматуры
Аs.
При одиночной гибкой
арматуре (![]() = 0) расчет производится по формуле
= 0) расчет производится по формуле
M£RScs+RbSbc; (67)
и положение нейтральной оси
определяется из уравнения
![]() . (68)
. (68)
5.33. Расчет изгибаемых
элементов комплексных конструкций на поперечную силу производится по формуле
Q£Rtwbz, (69)
где Rtw - расчетное сопротивление кладки
главным растягивающим напряжениям. принимаемое по табл. [10] и [11] и п.
[3.14];
b -
ширина сечения;
z - плечо внутренней пары
сил при прямоугольном сечении:
![]() . (70)
. (70)
В случае когда прочность
кладки при расчете на поперечную силу недостаточна, требуется установка хомутов
или часть продольных стержней отгибается в соответствии с указаниями СНиП
2.03.01-84.
ЭЛЕМЕНТЫ, УСИЛЕННЫЕ ОБОЙМОЙ
5.34. Несущая способность существующих
каменных конструкций (столбов, простенков, стен и др.) может оказаться
недостаточной при реконструкции зданий, надстройках, а также при наличии
дефектов в
кладке. Одним из наиболее эффективных методов повышения несущей способности
существующей каменной кладки является включение ее в обойму. В этом случае
кладка работает в условиях всестороннего сжатия, что значительно увеличивает ее
сопротивляемость воздействию продольной силы.
Применяются три основных вида
обойм: стальные, железобетонные и армированные растворные.
Основными факторами,
влияющими на эффективность обойм, являются: процент поперечного армирования
обоймы (хомутами), марка бетона или штукатурного раствора и состояние кладки, а
также схема передачи усилия на конструкцию.
С увеличением процента
армирования хомутами прирост прочности кладки растет непропорционально, а по
затухающей кривой.
Опытами
установлено, что кирпичные столбы и простенки, имеющие трещины, а затем
усиленные обоймами, полностью восстанавливают свою несущую способность.
5.35. Стальная обойма состоит из
вертикальных уголков, устанавливаемых на растворе по углам усиливаемого
элемента, и хомутов из полосовой стали или круглых стержней, приваренных к
уголкам. Расстояние между хомутами должно быть не более меньшего размера сечения
и не свыше 50 см (черт. 15, а).
Стальная обойма должна быть защищена от коррозии слоем цементного раствора
толщиной 25-30 мм. Для надежного сцепления раствора стальные уголки закрываются
металлической сеткой.
5.36. Железобетонная обойма
выполняется из бетона марок 150-200 с армированием вертикальными стержнями и
сварными хомутами. Расстояние между хомутами должно быть не свыше 15 см.
Толщина обоймы назначается по расчету и принимается от 6 до 10 см (черт. 15,б).
5.37. Обойма из раствора
армируется аналогично железобетонной, но вместо бетона арматура покрывается
слоем цементного раствора марки 50-100 (черт.
15, в).
Черт. 15. Схема усиления
кирпичных столбов обоймами.
а - металлической; б - железобетонной; в - армированной штукатуркой; 1 –
планка f1
сечением 35´5 - 60´12 мм; 2 - сварка; 3 - стержни диаметром 5-12 мм; 4 - хомуты диаметром
4-10мм; 5 - бетон класса В7,5 -В15; 6 - штукатурка (раствор марки 50-100)
5.38. Расчет конструкций из
кирпичной кладки, усиленной обоймами, при центральном и внецентренном сжатии
при эксцентриситетах, не выходящих за пределы ядра сечения, производится по
формулам:
при стальной обойме
при железобетонной обойме
при армированной растворной
обойме
![]() . (73)
. (73)
Коэффициенты y
и h принимаются при центральном сжтии y
= 1 и h = 1; при внецентренном сжатии (по аналогии с внецентренно
сжатыми элементами с сетчатым армированием):
![]() ; (74)
; (74)
В формулах (71) - (75):
N - продольная сила;
А - площадь сечения
усиливаемой кладки;
A¢s
- площадь сечения продольных уголков стальной обоймы или продольной арматуры
железобетонной обоймы;
Аb
- площадь сечения бетона обоймы, заключенная между хомутами и кладкой (без
учета защитного слоя);
Rsw - расчетное сопротивление поперечной арматуры обоймы;
Rsc - расчетное сопротивление уголков или продольной сжатой арматуры;
j - коэффициент продольного изгиба (при определении j значение a принимается как для неусиленной кладки);
mg - коэффициент, учитывающий влияние длительного воздействия нагрузки,
пп.[4.1, 4.7];
mk - коэффициент условий работы кладки, принимаемый равным 1 для кладки
без повреждений и 0,7 - для кладки с трещинами;
mb - коэффициент условий работы бетона, принимаемый равным 1 - при
передаче нагрузки на обойму и наличии опоры снизу обоймы, 0,7 - при передаче
нагрузки на обойму и отсутствии опоры снизу обоймы и 0,35 - без
непосредственной передачи нагрузки на обойму;
m - процент армирования
хомутами и поперечными планками, определяемый по формуле
где h и b - размеры сторон
усиливаемого элемента;
s -
расстояние между осями поперечных связей при стальных обоймах (h ³ s £ b, но не более 50 см) или
между хомутами при железобетонных и штукатурных обоймах (s£15 см).
5.39. Расчетные
сопротивления арматуры, применяемой при устройстве обойм, принимаются по табл.10.
|
Армирование |
Расчетные сопротивления
арматуры, МПа (кгс/см3) |
|
|
сталь класса A-I |
сталь класса A-II |
|
|
Поперечная арматура |
150 (1500) |
190 (1900) |
|
Продольная арматура без непосредственной передачи
нагрузки на обойму |
43 (430) |
55 (550) |
|
То же, при передаче нагрузки на обойму с одной
стороны |
130 (1300) |
160 (1600) |
|
То же, при передаче нагрузки с двух сторон |
190 (1900) |
240 (2400) |
5.40. С увеличением размеров
сечения (ширины) элементов при соотношении их сторон от 1:1 до 1:2,5
эффективность обойм несколько уменьшается, однако это уменьшение незначительно
и практически его можно не учитывать.
Когда одна из сторон
элемента, например, стена (черт. 16),
имеет значительную протяженность, то необходима установка дополнительных
поперечных связей, пропускаемых через кладку и располагаемых по длине стены на
расстояниях не более 2d и не более 100 см, где d -
толщина стены. По высоте стены расстояние между связями должно быть не более 75
см. Связи должны быть надежно закреплены. Расчет дополнительных поперечных
связей производится по формуле (72),
при этом коэффициент условий работы связей принимается равным 0,5.
Черт. 16. Схема усиления стены железобетонной обоймой
1 - металлическая сетка; 2 - дополнительные стержни, расположенные сверх сетки; 3 - хомуты (связи); 4 - бетон обоймы; 5 - кладка стены
Пример 8. Определение несущей
способности кирпичного столба с сетчатым армированием.
Определить расчетную несущую
способность и необходимое сетчатое армирование кирпичного столба размером в
плане 0,51´0,64 м с расчетной высотой 3
м. Расчетная продольная сила N = 800 кН (80 тc) и приложена с
эксцентриситетом е0=5 см в направлении стороны сечения столба,
имеющей размер 0,64 м. Столб выполнен из глиняного кирпича пластического
прессования марки 100 на растворе марки 75.
Площадь сечения столба А
=0,51×0,64 = 0,3264 м2.
Упругая характеристика кладки по п. [3.21, табл. 15] a=1000; коэффициент продольного изгиба по п.
[4.2, табл. 18] j=0,98. Расчетное
сопротивление кладки по п. [3.1, табл. 2] R=1,7 МПа (при А>0,3 м2).
Расчетную несущую способность Ncc для столба из
неармированной кладки определяем по формуле [13]
Ncc<mgj1RAcw = 1×0,97×1,7×0,3264×0,844×1,08×103=490 кH<N=800 кН.
j1, Ас и w определены по формулам [14] и [15], табл.
[19] п. [4.7]; mg=1, так как толщина столба более 30 см.
Расчетная несущая способность
столба Ncc оказалась в 1,7 раза меньше расчетной продольной силы N,
следовательно, необходимо усиление кладки сетчатым армированием.
Определяем необходимое Rskb=1,7×1,7 = 2,9 МПа.
Принимаем арматуру Вр-1
диаметром 4 мм. Расчетное сопротивление Rs =219 МПа по п. 5.6.
Процент сетчатого армирования
определяем по п. [4.31]
 %
%
По формуле [6] п. [3.20]
определяем
![]() МПа.
МПа.
Rsn=243 МПа принимается по п. 5.6.
По формуле [4] п. [3.20]
определяем
![]() .
.
При lhc=4,7 по формуле [15] и табл.
[18] пп. [4.2] и [4.7] определяем по интерполяции j=0,97;
jс=05 и j1=0,96.
По формуле [31] п. [4.31]
определяем
![]() МПа<2R=3,4 МПа.
МПа<2R=3,4 МПа.
Проверяем расчетную несущую
способность столба по формуле [30] п. [4.31]
![]() кН (83 тс > 80
тс).
кН (83 тс > 80
тс).
Дополнительно проверяем
расчетную несущую способность столба при центральном сжатии в плоскости,
перпендикулярной к действию изгибающего момента по формуле [27] п. [4.30]
![]() МПа > 2R=3,4 МПа
МПа > 2R=3,4 МПа
Принимаем Rsk = 3,4 МПа.
![]() .
.
По табл. [18] п. [4.2] j
= 0,96. По формуле [26] п. [4.30]
![]() кН >N = 800
кН (106 тc > 80 тc).
кН >N = 800
кН (106 тc > 80 тc).
Следовательно, расчетная
несущая способность столба, армированного сетчатой арматурой, при m=0,40%
достаточна.
Принимаем диаметр проволоки
для сеток 4 мм с расположением через два ряда кладки и исходя из 0,40%
армирования по табл. 9 определяем размер
ячейки в плане 3,2´3,2 см. Крайние стержни
располагаются от наружных граней столба (защитный слой) на 1,5 см.
Пример 9. Расчет усиления кирпичного
простенка стальной обоймой.
Требуется запроектировать
усиление простенка в существующем жилом доме. Кладка простенков выполнена из
глиняного кирпича пластического формования марки 75 на растворе марки 25.
Размер сечения простенка 54´103 см, высота 180 см;
расчетная высота стены - 2,8 м. Кладка простенка выполнена с утолщенными швами
низкого качества, в кладке имеются небольшие начальные трещины в отдельных
кирпичах и вертикальных швах. Это свидетельствует о том, что напряжение в
кладке достигло примерно 0,7Ru (временного сопротивления).
На простенок действует вертикальное усилие, равное 600 кН (60 тc),
приложенное с эксцентриситетом 5 см по отношению к толщине стены.
По архитектурным соображениям
усиление кладки принимается посредством включения простенка в стальную обойму
из уголков, согласно указаниям п. 5.35, 5.38.
Необходимое увеличение
несущей способности простенка за счет поперечной арматуры обоймы определяем из формулы (71):
![]() ,
,
где ![]() .
.
По п. [4.2, табл. 18] при l=5,2
и a=1000 j1»j=0,98; mg=1 принимаем согласно п. [4.7]; по п. [3.1, табл. 2] R=1,1
МПа; mk=0,7.
Принимаем для обоймы сталь
класса A-I. Вертикальная арматура обоймы (уголки) принимается
по конструктивным соображениям 41_50´50 мм
А¢s=4×4,8=19,2см2.
По табл. 10 Rsc=43,0 МПа и Rsw=150 МПа.
По формуле (75)
![]() .
.
Согласно формуле (71)
![]() ;
;
![]() ,
,
откуда m=0,35
%.
Принимаем расстояние между осями поперечных хомутов
обоймы 35 см и определяем их сечение из условия ![]() %.
%.
По формуле (76)
![]() ;
;
![]() ;
;
![]() см2.
см2.
Принимаем полосу сечением 30´8 мм; Аs=2,4 см2; Ст A-I.
Пример 10. В связи с надстройкой здания
требуется запроектировать усиление внутренней несущей кирпичной стены толщиной
в 1,5 кирпича (38 см). Высота стены от уровня пола до низа перекрытия сборного
настила 3,0 м. Кладка стены выполнена из сплошного глиняного кирпича
пластического формования марки 75 на растворе марки 25. Состояние кладки удовлетворительное.
После надстройки на 1 м стены будет передаваться нагрузка N = 750 кН (75т).
Aс=0,38 м2.
По табл. [2, 15 и 18], пп.
[3.1, 3.21, 4.2] R=1,1 МПа; a=1000; l=![]() =7,9; j=0,92; по формуле [16] п.
[4.7] mg=1.
=7,9; j=0,92; по формуле [16] п.
[4.7] mg=1.
Расчетная несущая способность
1 м стены
Ncc=jmgRA=0,92×1,1×0,38×103=385 кН<N=750 кН.
Требуется усиление стены,
которое осуществляем посредством включения стены в двухстороннюю железобетонную
обойму с установкой дополнительных поперечных стальных связей.
Толщину железобетонных стенок
по конструктивным соображениям принимаем минимальной, равной 6 см. Бетон класса
В12,5 и армирование стальной сеткой из стержней диаметром 5 мм с ячейкой 15´15 см. Кроме того, для обеспечения работы железобетонных стенок как
обоймы сверх сеток ставим вертикальные стержни из круглой стали диаметром 16 мм
через каждые 50 см и поперечные связи диаметром 16 мм через 50 см по высоте и
длине стены.
Расчетную несущую способность
1 м стены, усиленной железобетонной обоймой, определяем по формуле (72). При этом принимаем, что усилие
непосредственно на железобетонную обойму не передается; коэффициент условий
работы железобетона принимаем mb=0,35. При определении
поперечного армирования обоймы учитываем только поперечные связи диаметром 16
мм, расположенные через 50 см по длине и высоте стены.
Определяем процент
армирования поперечными связями:
![]() %,
%,
где Vs и Vk - соответственно объем
стержня (связей) и объем кладки;
А = 2,01 см2 -
площадь сечения одного стержня;
hw - толщина стены.
Вертикальное армирование
обоймы принято: Ст A-I, 7Æ5 мм в 2Æ16 мм на каждые 50 см длины стены. Площадь арматуры на 1 м стены
As¢=2(1,37+4,02)=10,78 см2;
Ab=2×6×100=1200 см2.
Коэффициент j
принимаем в запас прочности как для кирпичной кладки, учитывая высоту сечения с
учетом обоймы
a=1000; lh=![]() =6,25;
=6,25;
j=0,96; Rb=7,0 МПа.
По табл. 10 для связей Rs - 150 МПа.
По формуле (72) с учетом коэффициента условий работы 0,5
согласно п. 5.40 определяем расчетную
несущую способность

Таким образом, принятое
усиление стены достаточно.
6. РАСЧЕТ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ ПО
ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ВТОРОЙ ГРУППЫ
(ПО ОБРАЗОВАНИЮ И РАСКРЫТИЮ
ТРЕЩИН И ДЕФОРМАЦИЯМ)
6.1. Расчет элементов
конструкций по предельным состояниям второй группы производится по указаниям и
формулам, приведенным в пп. [5.1-5.5].
Расчет по раскрытию трещин
при учете особых нагрузок или воздействий не требуется.
6.2. Расчет каменных и
армокаменных конструкций по предельным состояниям второй группы производится:
по деформациям на воздействие
нормативных нагрузок;
по раскрытию трещин на
воздействие расчетных или нормативных нагрузок.
6.3. Если деформации
растяжения кладки вызваны перемещениями каркаса или ветровых поясов,
поддерживающих самонесущие или навесные стены, то предельные деформации
растяжения кладки принимаются равными єu=0,15×10-3 в зданиях с предполагаемым сроком службы конструкций не
менее 100 лет, єu=0,2×10-3 в зданиях с предполагаемым сроком службы конструкций не
менее 50 лет.
При наличии продольного
армирования в количестве m³0,03%, а также при оштукатуривании неармированных конструкций по сетке
приведенные выше значения єu увеличиваются на 25%.
6.4. При расчете по трещинам
конструкций из неармированной и армированной кладки, в которых раскрытие швов
может вызвать появление трещин в штукатурке, но не является опасным для
прочности и устойчивости конструкций, в формулах расчета на прочность по
растяжению всех видов Rt, Rtb и Rtw принимаются продольные силы и изгибающие
моменты по нормативным нагрузкам и коэффициенты условий работы по табл. [24].
Примечания: 1. Расчет по несущей
способности конструкций, указанных в п. 6.4,
следует производить с учетом расчленения конструкций после возникновения трещин
или образования шарниров в сечениях с раскрытием швов.
2. При невыполнении
требований расчета по трещинам, указанных в п.
6.4, в местах раскрытия швов необходимо предусматривать деформационные швы.
6.5. Расчет продольно армированных растянутых, изгибаемых и внецентренно
сжатых каменных конструкций по раскрытию трещин (швов кладки) следует
производить исходя из следующих предпосылок:
расчет производится для всего
сечения кладки и арматуры (без учета раскрытия швов), принимая закон линейного
распределения напряжений по сечению;
расчетные сопротивления
арматуры Rs, МПа (кгс/см2), принимаются по табл. 11.
6.6. При расчете продольно
армированных внецентренно сжатых, изгибаемых и растянутых каменных конструкций
по раскрытию трещин (швов кладки) сечение конструкций приводится к одному
материалу (стали) в отношении модулей упругости кладки и стали
Площадь сечения, расстояние
центра тяжести сечения до сжатой грани и момент инерции приведенного сечения
определяются по формулам:
Ared=nredA+As+As1; (78)
![]() ; (79)
; (79)
Ired=nredI+nredA(yred-y)2+As(h0-yred)2+As1(yred-a1)2. (80)
В формулах (77)-(80):
nred - отношение модулей упругости кладки и стали;
А, у, I - площадь сечения,
расстояние от центра тяжести сечения до сжатой грани и момент инерции сечения
кладки;
Ared, Vred, Ired - те же величины для
приведенного сечения;
As - площадь сечения растянутой арматуры;
As1 -
площадь сечения сжатой арматуры;
h0=h-а - рабочая высота сечения;
а
- расстояние от центра тяжести растянутой арматуры до растянутого края сечения;
а1
- расстояние от центра тяжести сжатой арматуры до сжатого края сечения.
|
Конструкции |
Условия работы |
Расчетные сопротивление
арматуры при предполагаемом сроке службы конструкций, лет |
||
|
100 |
50 |
25 |
||
|
Продольно армированные изгибаемые и растянутые
элементы в условиях агрессивной для арматуры среды |
Растяжение кладки в горизонтальном направлении (по
перевязанному сечению) |
42 (420) |
60 (600) |
60 (600) |
|
Растяжение кладки в вертикальном направлении (по
неперевязанному сечению) |
25 (250) |
35 (350) |
35 (350) |
|
|
Продольно армированные емкости при наличии
требований непроницаемости покрытий каменных конструкций |
Гидроизоляционная штукатурка |
17 (170) |
25 (250) |
35 (350) |
|
Кислотоупорная штукатурка на жидком стекле и
однослойное покрытие из плиток каменного литья на кислотоупорной замазке |
12 (120) |
15 (150) |
15 (150) |
|
|
Двух- и трехслойное покрытие из прямоугольных
плиток каменного литья на кислотоупорной замазке: |
|
|
|
|
|
растяжение вдоль длинной
стороны плиток |
30 (300) |
35 (350) |
35 (350) |
|
|
растяжение вдоль короткой
стороны плиток |
17 (170) |
25 (250) |
25 (250) |
|
6.7 Расчет по раскрытию трещин продольно
армированных каменных конструкций производится по формулам:
N£grRsAred; (81)
на изгиб
![]() ; (82)
; (82)
на внецентренное сжатие
на внецентренное растяжение
 . (84)
. (84)
В формулах
(81)-(84):
Rs - расчетное сопротивление арматуры оо раскрытию
треаетн;
N и М - продольная сила и момент от нормативных
нагрузок (при расчете конструкции по раскрытию трещин в штукатурных и плиточных
покрытиях усилия определяются по нормативным нагрузкам, которые будут приложены
после нанесения покрытия);
gr - коэффициент условия работы кладки при расчете по раскрытию трещин по
табл. [24] с учетом примечания к ней;
Ared, yred, Ired
– параметры приведенного сечения по формулам (78)-(80);
![]() - эксцентриситет
продольной силы N
- эксцентриситет
продольной силы N
7. УКАЗАНИЯ ПО ПРОЕКТИРОВАНИЮ КОНСТРУКЦИЙ
ОБЩИЕ УКАЗАНИЯ
7.1. Проектирование конструкций производится по
указаниям, приведенным в пп. [6.1-6.82] и в настоящем разделе.
7.2. Вертикальные и горизонтальные конструкции
здания (стены, столбы, рамы каркаса, перекрытия, покрытия и др.) образуют
пространственную систему, элементы которой воспринимают действующие на здание
нагрузки.
7.3.
Распределение усилий между элементами здания зависит от жесткости перекрытий
(материала, конструкции и длины участков перекрытий между поперечными
вертикальными конструкциями), толщины и высоты стен и наличия в них проемов,
материалов кладки [группы кладок, п. 65], а также от соединений между
конструктивными элементами здания.
КОНСТРУКТИВНЫЕ СХЕМЫ ЗДАНИЙ
7.4. К зданиям с жесткой
конструктивной схемой относятся здания, имеющие жесткие (неподвижные)
горизонтальные опоры в виде перекрытий, опирающихся на поперечные стены или
другие конструкции, удовлетворяющие требованиям п. [6.7 а, б, в].
Жесткую конструктивную схему
имеют, как правило, жилые дома и большая часть общественных зданий.
7.5. К зданиям с упругой
конструктивной схемой относятся здания, в которых расстояния между поперечными
стенами или другими жесткими опорами для перекрытий и покрытий превышают
указанные в табл. [27] при отсутствии ветровых связей, указанных в п. [6.7 в].
Независимо от расстояния
между поперечными конструкциями к упругим опорам относятся также покрытия из
легких конструкций (например, из асбестоцементных плит), опирающихся на
металлические или железобетонные фермы, прогоны, балки.
Упругую конструктивную схему
имеют, как правило, производственные, складские и сельскохозяйственные здания,
а также часть общественных зданий.
РАСЧЕТ СТЕН ЗДАНИЙ С ЖЕСТКОЙ КОНСТРУКТИВНОЙ СХЕМОЙ
7.6. Стены и столбы, имеющие в плоскостях
междуэтажных перекрытий жесткие опоры, рассчитываются согласно указаниям,
приведенным в пп. [6.10-6.14]. Эпюры изгибающих моментов при расчете стен как
неразрезных или однопролетных балок с шарнирными опорами приведены на черт. 17. Величины эксцентриситетов,
возникающих в стенах при действии вертикальных и горизонтальных (ветровых)
нагрузок относительно оси, проходящей через центр тяжести сечения стены,
определяются по формуле
![]() , (85)
, (85)
где М - изгибающий момент в
сечении;
N -
нормальная сила от вертикальной нагрузки.
Изгибающие моменты в стенах
учитываются от нагрузок, приложенных в пределах рассматриваемого этажа, т. е.
от перекрытия над этим этажом, балконов и т. п., а также от ветровой нагрузки.
Моменты от нагрузок вышележащих этажей учитываются, если сечение стены
изменяется в уровне перекрытия над данным этажом. При изменении сечения стены в
пределах рассчитываемого этажа следует учитывать момент, вызванный смещением
оси стены.
Расчетные формулы для
определения нормальных сил и моментов от вертикальных нагрузок приведены в табл. 12.
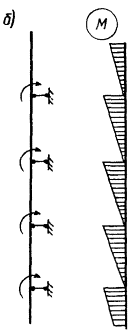
Черт. 17. Расчетные схемы и
эпюры изгибающих моментов от вертикальных внецентренно приложенных нагрузок
а - стена рассчитывается как неразрезная балка; б - стена рассчитывается в пределах каждого этажа как однопролетная балка
Указания по расчету сечений
на центральное и внецентренное сжатие приведены в пп. [4.7-4.11].
При одновременном действии
вертикальной и горизонтальной (ветровой) нагрузок в поперечных стенах (или на
отдельных участках между проемами) возникают усилия, приложенные с
эксцентриситетом в направлении продольной оси стены. Такие же эксцентриситеты
могут возникать при несовпадении равнодействующей вертикальных усилий с центром
тяжести рассчитываемого горизонтального сечения. Одновременно вертикальные
нагрузки могут создавать усилия, приложенные с эксцентриситетом в поперечном
направлении. В этом случае расчет сечений производится на косое внецентренное
сжатие по п. [4.12]. При наличии проемов в стенах усилия сжатия, возникающие в
простенках, определяются с учетом нагрузки, приложенной между осями соседних
проемов.
В стене с проемами каждый
простенок рассчитывается на нагрузку, соответствующую участку стены,
расположенному над этим простенком между осями соседних проемов. При этом не
учитывается возможное перераспределение этой нагрузки на соседние, менее
напряженные простенки через перемычки. Разгрузка этих простенков за счет
перераспределения нагрузки на смежные простенки не учитывается в связи с
возможным появлением трещин в перемычках при неравномерной осадке здания,
изменениях температуры и др.
Если на простенок опирается
сплошная стена (или стена с редкими нерегулярно расположенными проемами),
обеспечивающая перераспределение давления между простенками, то сечение стены
допускается рассматривать как одно целое с учетом ослаблений проемами (сечение
„нетто").
При этом если
равнодействующая вертикальных нагрузок приложена к центру рассчитываемого сечения,
то напряжения распределяются равномерно по длине сечения; если же
равнодействующая смещена по отношению к центру сечения (например, при
несимметричном расположении проемов), то при расчете следует учитывать
эксцентриситет в плоскости стены.
7.7. Расчет стен зданий на
ветровые нагрузки, направленные параллельно стенам, производится в
последовательности:
определяются расчетные
значения ветровой нагрузки;
производится распределение
ветровой нагрузки между поперечными или продольными стенами, расположенными в
направлении действия нагрузки;
определяются усилия
(напряжения), возникающие в стенах здания и их элементах (перемычках,
соединениях) при действии ветровой нагрузки.
Величины нормативной и
расчетной ветровой нагрузок определяются по СНиП 2.01.07-85.
7.8. Ветровая распределенная
нагрузка на j-ю стену здания определяется по формуле
где qj - нагрузка на 1 м высоты
рассчитываемой стены j на рассматриваемом уровне по
высоте здания;
q -
интенсивность ветровой нагрузки, МПа (кгс/м2 ), на том же уровне;
v1 и v2 - коэффициенты, зависящие от
вида перекрытия: при монолитном железобетонном перекрытии v1=0,9 и v2=0,1; при сборных
замоноличенных перекрытиях v1=0,65 и v2=0,35; при деревянных
перекрытиях v1=0,1 v2=0,9;
Lj-1+Lj - расстояния между рассматриваемой j-й стеной и соседними стенами
(справа и слева);
di и dj - горизонтальные перемещения
стен на уровне 2/3 высоты стены относительно планировочной отметки земли,
вызванные равномерно распределенной по высоте этих стен нагрузкой q=1;
|
Конструкция
стены, расчетные схемы и эпюры моментов |
Формулы |
|
|
Nx=N+N1+N2;
|
|
|
Nx=N+N1+N2;
|
|
|
Nx=N+N1+N2; M1=N1e1;
|
Обозначения, принятые в табл.
12:
N - сумма расчетных нагрузок на стену, расположенных выше
рассматриваемого этажа. В величину включается также продольное усилие от
действия ветровой нагрузки, если она учитывается в расчете;
N1 - расчетная
величина опорного давления перекрытия над рассматриваемым этажом;
N2 - расчетное
значение собственного веса участка стены между рассматриваемым сечением и
расположенным выше этажом;
М - расчетный изгибающий
момент;
Nx и
Мx - нормальная сила и изгибающий момент в
рассчитываемом сечении стены.
Примечание. Моменты от ветровой
нагрузки, действующей в пролете стены между перекрытиями, определяются по п.
[6.10].
l - длина
здания в направлении, перпендикулярном давлению ветра;
w - число
стен, параллельных направлению ветра.
Перемещения следует
определять с учетом деформаций изгиба, а при отношении высоты стены H к
высоте сечения h£10 - также и с учетом деформаций сдвига. При
вычислении прогибов относительные деформации сдвига у вычисляются по формуле
![]() , (87)
, (87)
где Q - поперечная сила в
рассматриваемом сечении;
G -
модуль сдвига кладки (G=0,4E0);
А - площадь сечения;
К - коэффициент, учитывающий
влияние неравномерности распределения касательных напряжений на деформации
изгибаемого элемента (для сечений, состоящих из нескольких прямоугольников в
плане), в общем случае определяется по формуле
здесь А и I0 - площадь сечения и момент
инерции относительно оси х, проходящей через центр тяжести сечения;
y1 и y2- ординаты верхней и нижней
границы сечения;
S(y) -
статический момент части площади сечения от уровня у до края сечения
относительно оси сечения;
b(y) -
ширина сечения на уровне у.
Для прямоугольного сечения
коэффициент К принимается равным 1,2.
При значительной разнице в
жесткости стен одного направления более жесткие стены 1 (черт. 18) могут рассматриваться как диафрагмы жесткости
зданий, воспринимающие всю ветровую нагрузку. При этом участки малой жесткости
стены 2 (см. черт. 18) допускается не
учитывать.
Черт. 18. Схема поперечных
стен здания
1 - диафрагмы; 2 - стены
малой жесткости
Ветровые нагрузки,
воспринимаемые диафрагмами, определяются по формуле (86) при значениях v1 и v2, указанных выше, при этом
учитывается сумма характеристик жесткости ![]() всех диафрагм.
всех диафрагм.
7.9. Каждая стена рассматриваемого
направления рассчитывается как консоль, заделанная в основании под действием
горизонтальных нагрузок от активного и пассивного давления ветра.
Расчет поперечных стен на
главные растягивающие напряжения от горизонтальной (ветровой) нагрузки
производится по формулам, приведенным в пп. [6.12; 6.13].
7.10. Если
стена имеет расположенные друг над другом проемы (например, дверные), то она
рассматривается как система вертикальных консолей (полос между проемами),
связанных друг с другом перемычками. При расчете, как правило, перемычка
рассматриваются как абсолютно жесткие ригели (распорки), шарнирно связанные со
стенами [п. 6.14]. При этом расчет перемычек производится только на
вертикальные нагрузки, расположенные над ними. В этом случае нагрузку,
воспринимаетмую каждым участком (вертикальной полосой) стены, допускается
определять по формуле
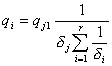 , (89)
, (89)
где qj – горизонтальная распределенная нагрузка, воспринимаемая рассчитываемой
стеной j;
qj1 – горизонтальная распределенная нагрузка, воспринимаемая рассчитываемым
участком j1 стены j;
dj – прогиб рассчитываемого j-го участка стены при единичной распределенной нагрузке в уровне 2/3
высоты стены;
di – то же, для участка стены i;
r – число вертикальных участков, на которые стена
разделена проемами.
В поперечных стенах с проемами число этих участков
обычно равно двум или трем, а в продольных – более трех.
Прогибы следует определять с учетом указаний п. 7.8.
Расчет стены с проемами с учетом совместной работы
вертикальных участков стен (полос между проемами) допускается при условии
достаточной прочности перемычек, воспринимающих изгибающие моменты и поперечные
силы, что должно быть подтверждено расчетом, см. пп. [6.14; 6.15].
При нерегулярном расположении в стене отдельных
проемов, разделенных перемычками с отношением H/l³0,75 (H и l – высота и пролет перемычки) при площади «нетто»
любого вертикального или горизонтального сечения, составляющей не менее 70% его
полной площади, допускается при определении усилий рассчитывать стену как
сплошную. При расчете на прочность сечений, пересекающих проемы, принимаются
момент инерции, момент сопротивления и площадь сечения «нетто».
7.11. Если стены взаимно перпендикулярного
направления соединены перевязкой или другими достаточно жесткими и прочными
связями, то следует учитывать совместную работу рассчитываемой стены и участков
примыкающих к ней стен. В этом случае расчетное горизонтальное составное
сечение может иметь форму двутавра, швеллера, тавра и т.п. Достаточная
прочность или трещиностойкость перевязки или соединений должна быть
подтверждена расчетом на горизонтальные и вертикальные нагрузки [п. 6.11]. При
учете совместной работы поперечных и продольных стен при действии
горизонтальной нагрузки, в случае если поперечная и продольная стены выполнены
из материалов различной жесткости, при вычислении А и I принимается ширина полки bred, приведенная к материалу поперечной стены по
формуле
![]() , (90)
, (90)
где b - ширина полки;
Е2
- модуль
деформаций материала полки (например, кладки учитываемого участка продольной
стены);
Е1 - модуль
деформаций материала стенки (кладки рассматриваемого участка поперечной
стенки).
При соединении стен гибкими
(металлическими) связями, при расчете на ветровую нагрузку участки стен
перпендикулярного направления не включаются в сечение рассчитываемой стены. В
случае необходимости связь между примыкающими стенами может быть обеспечена
рассчитанными на сдвиг железобетонными или металлическими шпонками.
7.12. Поперечные стены,
воспринимающие действующие в их плоскости горизонтальные (ветровые) нагрузки,
должны быть рассчитаны на главные растягивающие напряжения по пп. [6.12; 6.13].
Если прочность поперечных стен с проемами обеспечивается только с учетом
жесткости перемычек, то перемычки должны быть рассчитаны на возникающие в них
перерезывающие силы, см. пп. [6.14; 6.15].
При расчете стен на
горизонтальные нагрузки, действующие в их плоскости, расчетную ширину полок
составных сечений следует принимать по указаниям, приведенным в п. [6.9].
РАСЧЕТ СТЕН ЗДАНИЙ С УПРУГОЙ КОНСТРУКТИВНОЙ СХЕМОЙ
7.13. При упругих опорах
(здания с упругой конструктивной схемой), см. п. [6.8], производится расчет
рамной системы, стойками которой являются стены и столбы (железобетонные,
кирпичные и др.), а ригелями - перекрытия и покрытия, которые рассматриваются
как жесткие распорки, шарнирно связанные со стенами. При упругих опорах
принимается, что стойки заделаны в грунт в уровне пола здания (при наличии
бетонного подстилающего слоя под полы и отмостки).
7.14. В зданиях с упругой
конструктивной схемой жесткость стен или столбов, выполненных из кирпичной или
каменной кладки, при статическом расчете рамы определяется, принимая модуль
упругости кладки Е=0,8Е0.
7.15. При значительных
сосредоточенных нагрузках (таких, как опорные реакции ферм, балок больших
пролетов, прогонов, подкрановых балок и пр.) стены, как правило, усиливаются
пилястрами.
В этом случае стойки имеют
тавровое сечение. Если нагрузка от перекрытия или покрытия распределена
равномерно по длине стены (например, при покрытии из железобетонного настила),
за ширину полки может приниматься вся ширина простенка или же, при глухих
стенах, - вся длина стены между осями примыкающих к пилястре пролетов.
Если нагрузка от перекрытия
сосредоточена на отдельных участках (опирание ферм, балок и пр.), при статическом
расчете допускается принимать ширину полки тавра согласно указаниям п. [6.9].
Если толщина стены меньше 0,1 высоты сечения пилястры, то сечение
рассматривается как прямоугольное без учета примыкающих участков стены.
7.16. Каждая поперечная рама,
состоящая из вертикальных и горизонтальных элементов, расположенных на одной
оси, рассчитывается, как правило, независимо от других рам, если нет
специальных условий, при которых возможна существенная перегрузка какой-либо
рамы при загрузке других пролетов. Расчет производится на все нагрузки,
расположенные между средними осями пролетов здания, примыкающих к
рассчитываемой раме.
7.17. Расчет стен и столбов
законченного здания упругой конструктивной схемы производится с учетом разных
условий работы этих элементов при нагрузках, приложенных до и после установки
перекрытий. Стены и столбы рассчитываются на нагрузки, приложенные до установки
перекрытий или покрытий (собственный вес стен, некоторые виды оборудования и
др.) как свободно стоящие стойки, заделанные в грунт. На нагрузки, приложенные
после устройства перекрытий, стены и столбы рассчитываются как элементы рам.
Усилия, вычисленные при этих двух нагрузках, суммируются.
Опорные реакции в шарнирной
верхней опоре каждой стойки определяются последовательно от всех приложенных
нагрузок, и полученные значения суммируются.
Примечание.
Расчет
однопролетных и многопролетных рам с шарнирно опертыми ригелями и ступенчатыми
защемленными стойками может производиться по таблицам справочников.
РАСЧЕТ СТЕН МНОГОЭТАЖНЫХ ЗДАНИЙ ИЗ КИРПИЧА ИЛИ КЕРАМИЧЕСКИХ КАМНЕЙ НА ВЕРТИКАЛЬНУЮ НАГРУЗКУ ПО РАСКРЫТИЮ ТРЕЩИН ПРИ РАЗЛИЧНОЙ ЗАГРУЗКЕ ИЛИ РАЗНОЙ ЖЕСТКОСТИ СМЕЖНЫХ УЧАСТКОВ СТЕН
7.18. При различии наружных и
примыкающих к ним внутренних стен по степени загрузки или выполнении их из
различных материалов (например, из силикатного и глиняного кирпича или
керамических камней) участки стен, близкие к местам их взаимного примыкания,
должны быть рассчитаны по образованию и раскрытию трещин.
7.19. При расчете условно
принимается, что обе стены (или смежные участки одной и той же стены) не
связаны друг с другом, и определяется свободная деформация каждой из двух стен
отдельно при действии расчетных длительных нагрузок. Разность свободных
деформаций этих стен должна удовлетворять условию
d1-d2£du, (91)
где d1 -
абсолютная свободная деформация сжатия одной из стен (или участка стены);
d2 -
то же, второй стены;
du - предельная допустимая
разность деформаций согласно табл. 13.
Величины свободных деформаций
определяются как сумма деформаций кладки во всех этажах здания от уровня верха
фундамента до верха стены по формулам:
|
Число этажей |
5 |
6 |
7 |
8 |
9 |
12 и более |
|
Высота стены, H |
15 |
18 |
21 |
24 |
27 |
36 и более |
|
du,
мм |
7 |
8 |
9 |
10 |
12 |
15 |
![]()
где s1i - напряжения в кладке первой свободно стоящей стены в i-м этаже;
s2i - то же, второй стены;
E1i -
модули деформация кладки первой стены на 1-м этаже;
E2i -
то же, второй стены;
hi - высота i-го этажа;
dsh1 и
dsh2 -
абсолютные деформации усадки первой и второй стены, вычисленные по
относительным значениям усадок материалов стен [см. п. 3.26], умноженным на
высоту соответствующих участков стен;
n - число
этажей от пола подвала до верхнего или рассматриваемого промежуточного этажа.
Напряжения определяются в
середине каждого этажа и вычисляются при расчетных значениях всех длительных
нагрузок. Модули упругости Ei входящие в формулы (92), вычисляются во
формуле [1] п. [3.20]
Ei=a1iRiu, (93)
где Riu - средний предел прочности
кладки первой или второй стены данного этажа, принимаемый по формуле [3] п.
[3.20] для кладки, возводимой в летних условиях;
a1i -
характеристика деформаций, которая зависит от материала кладки и учитывает полные
деформации кладки (без учета деформаций усадки).
Значение характеристики a1 для кладки на растворе марки
25 и выше приведено в табл. 14.
7.20.
Совместная работа стен и распределение усилий с нагруженной стены на менее
нагруженную или менее деформированную во многом зависит от конструктивной схемы
здания. Оптимальным решением являются следующие схемы: опершие плит перекрытий
по четырем или трем: сторонам; опирание плит перекрытий поочередно - на одном
этаже на внутренние стены, на другом- на наружные.
|
Кладка |
a1 для кладки |
|
|
летней |
зимней после затвердевания |
|
|
Из кирпича: |
|
|
|
глиняного пластического
прессования |
450 |
300 |
|
силикатного и глиняного
полусухого прессования |
250 |
170 |
|
Из керамических камней высотой 140 мм |
650 |
430 |
Примечание. При зимней кладке,
выполняемой на растворах с противоморозными химическими добавками, значения
характеристики деформаций принимаются такими же, как для летней кладки.
В этих случаях усилие
распределяется на внутренние и наружные стены более равномерно и уменьшается
вероятность появления трещин в стенах. Кроме того, уменьшается нагрузка на
стены и фундаменты.
Следует также учитывать, что
для уменьшения разности деформаций стен и повышения жесткости здания следует
заводить продольные края плит перекрытий в несущую стену на 8-10 см. Это
частично перераспределит усилие на стены и обеспечит лучшую их совместную
работу.
В этом случае
разницу в деформациях стен, определяемую по формулам (92), допускается уменьшить в 1,5 раза, когда
свободная длина несущих стен до пересечения их с внутренними продольными
ненесущими стенами или отрезками стен не превышает 7,5 м, и в 1,25 раза - при
свободной длине более 7,5 м.
7.21. Приведенный в п. 7.19 расчет ограничивает возможность
раскрытия трещин, но не исключает полностью вероятность их появления. Трещины
также могут появиться в результате неравномерной осадки фундаментов,
температурных воздействий, усадки и др. Поэтому для обеспечения совместной
работы стен и перекрытий при проектировании зданий должны быть предусмотрены
следующие конструктивные мероприятия. В зданиях высотой более 5 этажей
рекомендуется устраивать под перекрытиями или между торцами опирающихся на
стены плит перекрытий армокаменные пояса, укладываемые по наружным и внутренним
стенам. Пояса укладываются начиная с 5-го этажа через три этажа до
предпоследнего.
В наружных стенах
рекомендуется вместо устройства поясов укладывать под опорами перемычек
арматурные сетки по всей ширине простенков.
В этажах, где пояса не
предусматриваются, в пересечениях стен необходимо под перекрытиями укладывать
связевые арматурные сетки из продольных стержней диаметром 8 мм и поперечных -
4 мм с размером ячейки 100´100 мм. Для того чтобы
избежать утолщения растворных швов в пересечениях сеток, а также в целях
обеспечения технологичности их изготовления допускается укладывать сетки в
смежных по высоте рядах кладки стен разного направления. В несущих стенах сетки
должны заходить за грань первой плиты перекрытий, опирающихся на стену не менее
чем на 50 см.
Связи не
должны пересекать дымовые и вентиляционные каналы, в этих местах их следует
предусматривать двухветвевыми с укладкой каждой ветви в верстовых рядах кладки.
Для кладки стен многоэтажных
зданий (9 этажей и выше) следует применять растворы не ниже марки 50.
УЧЕТ ЗАПОЛНЕНИЯ (СТЕН)
КАРКАСНЫХ ЗДАНИЙ ПРИ РАСЧЕТЕ КАРКАСОВ
7.22. При оценке
перемещений каркасных стен для определения периода собственных колебаний
каркасных зданий, вызванных ветровой нагрузкой, допускается учитывать работу
заполнения из кирпичной или каменной кладки при условии применения раствора
марки не ниже 50 и при толщине стены не менее 25 см. При расчете каркаса по
несущей способности заполнение следует учитывать только как нагрузку.
7.23. В случае, указанном в п. 7.22, допускается повышать поэтажные
жесткости каркаса при определении части деформаций, вызванных поперечной силой
(сдвигом).
Расчетное значение горизонтальной
поперечной силы в заполнении (черт. 19)
не должно превышать величины
где l - длина заполнения панели
каркаса;
h -
толщина заполнения;
![]() - применение формулы (94) допускается при
удовлетворении неравенства 0,8£b£2;
- применение формулы (94) допускается при
удовлетворении неравенства 0,8£b£2;
Rsq - расчетное сопротивление срезу (касательное сцепление) по
неперевязанному сечению (см. табл. [10]);
a
- коэффициент, принимаемый равным 0,4 для кладки из сплошного кирпича и 0 - для
кладки из пустотелого кирпича;
g
- коэффициент, учитывающий влияние проема: для сплошного заполнения равен 1;
для заполнения с проемом шириной l1£0,6l и высотой H1£0,65H (см. черт.
19, б) при условии H1/l £2 (l2 - ширина простенка) его можно определять по формуле
![]() . (95)
. (95)
7.24. Жесткость зданий с
металлическим или железобетонным каркасом и с заполнением из каменной кладки
должна отвечать следующим требованиям:
горизонтальные перемещения
верха здания по отношению к отметке верха фундамента, определяемые без учета
поворота фундамента, не должны превышать 1/1000 высоты здания;
Черт. 19. К расчету каркасных
стен
а - общий вид
каркасной стены с заполнением панелей каркаса кладкой; б - схема заполнения с
проемами
эти же перемещения,
определяемые с учетом поворота фундамента, не должны превышать 1 /750 высоты
здания;
перекосы панелей каркаса
(заполненных каменной кладкой), вызванные поперечной силой, должны быть не
более 1/1500.
ДОПУСТИМЫЕ ОТНОШЕНИЯ ВЫСОТ СТЕН И СТОЛБОВ К ИХ ТОЛЩИНАМ
7.25 Предельные отношения высот
стен, столбов и перегородок к их толщинам, независимо от результатов расчета,
не должны превышать указанных в пп. [6.16-6.20].
Примечание. Как столбы, с учетом
коэффициентов, приведенных в табл. [30], рассматриваются участки кладки, ширина
которых не превышает утроенной толщины.
7.26 В зданиях с открывающимися проемами внутренние стены и перегородки,
помимо воспринимаемых ими нагрузок, следует рассчитывать на ветровую нагрузку
согласно СНиП
2.01.07-85.
7.27. Если толщина стен или
перегородок назначена с учетом опирания по контуру, необходимо предусматривать
их крепление к примыкающим боковым конструкциям и к верхнему покрытию или
ригелю каркаса с помощью перевязки кладки, анкеров, заделки в борозду кладки,
заделки между шипами швеллеров, двутавровых профилей и т. п.
В многоэтажных зданиях
закрепление несущих стен вверху в каждом этаже обеспечивается опирающимися на
них перекрытиями.
Пример 11. Найти
распределение ветровой нагрузки между поперечными стенами 12-этажного жилого
дома. Длина здания 66 м; высота 38 м.
Схематический план и разрез
по наружной стене здания приведены на черт.
20, а горизонтальные сечения всех
участков стены на черт. 21.
Перекрытия сборные
железобетонные, замоноличенные. Расчет производится по указаниям п. 7.8 и по формуле (86). Нумерация стен приведена на черт. 20.
Черт. 20. Схема здания
а - план; б - поперечный
разрез
Так как при расчете распределения
ветровой нагрузки прогибы стен определяются на высоте 2/3H=25,3 м,
а толщина стены уменьшается на уровне 21,6 м, то это изменение сечения стены
практически не влияет на величину прогиба. Поэтому находим I0 (момент инерции относительно
оси, проходящей через центр тяжести сечения стены) и коэффициент К (для
вычисления прогибов от действия поперечной силы) только для сечений стен в
нижних этажах.
Приводим
вычисление величин I0 и К для сложного сечения стены № 1.
Площадь сечения
А=9,62×0,64+1,10×0,64+(1,20+2,95)×0,64=9,50 м2.
Статический момент
относительно верхнего края сечения
![]() м3.
м3.
Расстояние от верхнего края
сечения до его центра тяжести
![]() м.
м.
Момент инерции относительно
верхнего края сечения (пренебрегая очень малыми моментами инерции
горизонтальных участков относительно их собственной оси)
![]() м4.
м4.
Момент инерции относительно
оси, проходящей через центр тяжести сечения
I0=314-9,50×5,122=65м4.
Коэффициент К
определяем по формуле (88):
Dup=D3;
Dl=D4,
где участки D3 и D4 - см. черт. 22;
![]() ;
;
![]() м3;
м3;
S*2 = 53,83 м6;
h = 3,38 м; h3 = 38,6 м3; h5 = 441 м5;
b = 0,64 м; b2 = 0,4096 м2;
![]() м6
м6
Формула для определения D4, та же, что для D3.
![]() м3;
м3;
S*2 = 108,2 м6;
h = 1,39; h3 =
2,68; h5 =5,18 м5;
b = 0,64 м; b2 = 0,4096 м2;
Черт. 21.Сечение стен.
Черт. 22. Схема для определения коэффициента К стены № 1
![]() м6;
м6;
![]() .
.
Вычисление значений К для
остальных стен производится по той же методике, что и для стены № 1, и здесь не
приводится.
Коэффициенты К вычисляются
для стен, у которых отношение высоты стены к высоте сечения H/h<10.
Величина А, I0 и К для всех стен, а также другие характеристики сечений, необходимые
для расчета, приведены в табл. 15.
Определяем горизонтальные
перемещения (прогибы) d стен на уровне 2/3H,
являющиеся условной характеристикой жесткости стен при изгибе в их плоскости.
Обозначаем через x
расстояние от уровня заделки стены до рассматриваемого сечения.
Прогиб консоли при равномерно
распределенной нагрузке от действия изгибающих моментов.
 .
.
На уровне ![]()
![]() .
.
Прогиб той же консоли от
действия поперечных сил
![]() .
.
На уровне ![]()
![]() .
.
Модули упругости для всех
стен приближенно принимаем постоянными. Модуль сдвига согласно п. [3.27] G=0,4E.
Нагрузка q = 1.
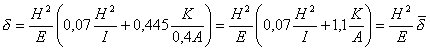 .
.
Величина ![]() является общей для
всех стен и при применении формулы
(86) сокращается. Величина
является общей для
всех стен и при применении формулы
(86) сокращается. Величина
0,07H2=0,07×362»0,91×102.
|
Номер стены |
Число стен ni |
А, м2 |
I0, м4 |
К |
|
|
|
|
F |
||
|
1 |
1 |
9,50 |
65 |
1,86 |
1,4 |
0,215 |
1,62 |
0,6173 |
0,124 |
||
|
2 |
1 |
4,46 |
0,77 |
- |
118,2 |
- |
118,2 |
0,00846 |
0,0017 |
||
|
3 |
1 |
2,69 |
0,91 |
- |
100 |
- |
100 |
0,01 |
0,02 |
||
|
4 |
2 |
2,78 |
1,83 |
- |
49,6 |
- |
49,6 |
0,0202 |
(0,0404) |
0,0041 |
(0,0082) |
|
5 |
1 |
4,51 |
31,8 |
- |
2,9 |
0,43 |
3,33 |
0,3003 |
- |
0,0604 |
- |
|
6 |
2 |
4,26 |
29,9 |
1,78 |
3,0 |
0,426 |
3,43 |
0,292 |
0,584 |
0,0586 |
(0,1172) |
|
7 |
4 |
1,99 |
1,1 |
1,65 |
82,8 |
- |
82,9 |
0,0121 |
0,0484 |
0,00243 |
(0,00972) |
|
8 |
2 |
6,02 |
56,4 |
- |
1,61 |
0,258 |
1,87 |
0,5348 |
1,07 |
0,1077 |
(0,2154) |
|
9 |
1 |
2,31 |
0,54 |
1,41 |
169 |
- |
169 |
0,0059 |
- |
0,0012 |
- |
|
10 |
1 |
7,03 |
22,1 |
- |
4,1 |
0,38 |
4,48 |
0,2232 |
0,0448 |
||
|
11 |
1 |
4,05 |
5,1 |
2,43 |
17,9 |
- |
17,9 |
0,0559 |
0,0112 |
||
|
12 |
1 |
7,20 |
43,8 |
- |
2,1 |
0,316 |
2,42 |
0,414 |
0,0833 |
||
|
13 |
1 |
7,33 |
11,4 |
2,07 |
8,0 |
- |
8,0 |
0,125 |
0,0251 |
||
|
14 |
1 |
6,77 |
43,4 |
1,85 |
2,1 |
0,3 |
2,4 |
9,416 |
0,0838 |
||
|
15 |
1 |
6,47 |
126 |
1,38 |
0,72 |
0,235 |
0,95 |
1,053 |
0,212 |
||
|
|
|
|
|
|
|
|
|
|
SF=1,000 |
||
Вычисляем поэтому для всех
стен
![]() (все величины в м).
(все величины в м).
Формула (86) может быть представлена в следующем виде
 ,
,
где ql - ветровая нагрузка на
горизонтальную расчетную полосу здания в рассматриваемом уровне высоты здания;

С=Fv1+Bv2.
Вычисление величин ![]() , и коэффициентов F приведено в табл.15.
, и коэффициентов F приведено в табл.15.
Как видно из черт. 20 и табл.15, стены 1; 5; 6; 8; 12; 14 и 15 являются наиболее
жесткими. Эти стены рассматриваются нами как диафрагмы жесткости и для них в табл. 16 вычислены коэффициенты B.
В табл. 16 приведены величины ветровых нагрузок на каждую
из диафрагм, вычисленные при значениях v1=0,65 и v2=0,35.
Из табл. 15 и 16
видно, что при распределении по жесткостям стен девять диафрагм воспринимают
89%, а остальные 12 стен малой жесткости - только 11% всей ветровой нагрузки.
При распределении же по формуле (86) с учетом расстояний
между диафрагмами на них передается 93,5% нагрузки.
Распределение ветровой
нагрузки между стенами малой жесткости производится при значениях v1=1 и v2=0, т.е. только
пропорционально характеристикам жесткости стен. Для этих стен
qj=Fql кН/м.
Следует иметь в виду, что
суммарная нагрузка на все стены будет немного больше (в нашем случае на 4,4%),
чем ql. Это объясняется тем, что для стен малой жесткости принимается
коэффициент v1=1, а не v1=0,65. Повышенное значение
учитывает возможность некоторого прогиба перекрытий, а также условность
передачи 35% всей ветровой нагрузки по грузовым площадям на диафрагмы.
Для определения изгибающих
моментов в поперечных стенах может быть принята непрерывная неравномерно
распределенная, изменяющаяся по высоте здания ветровая нагрузка или же
нагрузка, равномерно распределенная в пределах зон, высота которых не должна
превышать 10 м, или же (при расчете многоэтажных зданий) распределенные
нагрузки могут быть заменены сосредоточенными в уровне каждого этажа. Примем
последний вариант расчета и определим расчетные сосредоточенные силы,
приложенные к каждой стене, например (см. черт. 20, б) перекрытия над шестым этажом, т.е. на
высоте 2,4+6×2,8=19,2 м. Расчет производим
для I ветрового района СССР. Скоростной напор ветра равен w0=0,27 кН/м2, и
нормативное значение ветровой нагрузки
wm=w0kc=0,27×1,2×1,4=0,45 кН/м2,
где k=1,2 - коэффициент,
учитывающий изменение скоростного напора ветра на высоте 20 м;
с=1,4 - аэродинамический
коэффициент, учитывающий положительное и отрицательное давление ветра на
здание.
Расчетная ветровая нагрузка
на 1 м2 стены в рассматриваемом уровне
qр=1,2wm=1,2×0,45=0,54 кН/м2.
В уровне перекрытия
приложена нагрузка, соответствующая горизонтальной полосе шириной, равной
высоте этажа 2,8 м.
Таким образом, расчетная
нагрузка в уровне перекрытия на 1 м длины здания равна:
q=0,54×2,8=1,51 кН/м.
При длине здания l=66 м
Q6=ql=1,51×66=100
кН.
Распределение нагрузки между
стенами здания приведено на основании данных табл. 15 - 17; Q -
сосредоточенные нагрузки на каждую из стен на уровне перекрытия над шестым
этажом. В остальных этажах нагрузка может быть вычислена по формуле Q=ki/k6, где ki и k6 - значения коэффициентов k для
рассматриваемого и для шестого этажей.
|
Номер |
Расстояние между осями
диафрагм, м |
|
|
F (по табл. 15) |
0,65 F |
0,35 B |
С |
||
|
диафрагмы |
стены |
оси |
|||||||
|
I |
1 |
1 |
- |
4,77 |
0,0726 |
0,1240 |
0,0806 |
0,0254 |
0,1060 |
|
II |
5 |
2 |
9,54 |
5,72 |
0,0868 |
0,0640 |
0,0392 |
0,0304 |
0,06996 |
|
III |
6 |
3 |
1,89 |
5,05 |
0,0759 |
0,0586 |
0,0381 |
0,0266 |
0,0647 |
|
IV |
8 |
4 |
8,22 |
10,45 |
0,1587 |
0,1077 |
0,0700 |
0,0555 |
0,1255 |
|
V |
12 |
6 |
12,68 |
13,35 |
0,2027 |
0,0833 |
0,0542 |
0,0770 |
0,1312 |
|
VI |
8 |
9 |
14,02 |
11,12 |
0,1684 |
0,1077 |
0,0700 |
0,0590 |
0,1290 |
|
VII |
6 |
10 |
8,22 |
6,68 |
0,1012 |
0,0586 |
0,0381 |
0,0354 |
0,0735 |
|
VIII |
14 |
1 |
5,13 |
5,71 |
0,0858 |
0,0838 |
0,0545 |
0,0300 |
0,0845 |
|
IX |
15 |
12 |
6,3 |
3,15 |
0,0479 |
0,2120 |
0,1380 |
0,0167 |
0,1547 |
|
|
|
|
|
|
|
|
|
Итого |
0,9387 |
|
Номер стены |
Распределение ветровой
нагрузки Q6=ql=100 кН между стенами здания на уровне
перекрытия над шестым этажом |
|
|
С |
Q, кН |
|
|
1 |
0,1060 |
10,6 |
|
2 |
0,0017 |
0,17 |
|
3 |
0,0020 |
0,20 |
|
4 |
0,0041 |
0,41 |
|
5 |
0,0696 |
6,96 |
|
6 |
0,0647 |
6,47 |
|
7 |
0,0024 |
0,24 |
|
8 |
0,1255 |
12,55 |
|
9 |
0,0012 |
0,12 |
|
10 |
0,0448 |
4,48 |
|
11 |
0,0112 |
1,12 |
|
12 |
0,1312 |
13,12 |
|
13 |
0,0251 |
2,51 |
|
14 |
0,0845 |
8,45 |
|
15 |
0,1547 |
15,47 |
Пример 12. Определение изгибающих
моментов в поперечной стене многоэтажного здания при действии ветровой
нагрузки.
Здание 12-этажное высотой H=38 м.
Рассчитываемая поперечная стена, а также примыкающие к ней участки наружной
стены имеют постоянную жесткость B1 в первых семи этажах и
жесткость B2 в верхних пяти этажах. Жесткость в верхних этажах
уменьшается вследствие изменения толщины стены; модуль упругости кладки во всех
этажах одинаков, и поэтому В1 и B2 пропорциональны моментам
инерции сечений I1 и I2.
Поперечная стена разделена
дверными проемами (черт. 23, а) на
три вертикальных участка, сечения которых показаны на черт. 23, б; размеры без скобок относятся к семи нижним
этажам, в скобках - к пяти верхним.
Стена должна быть рассчитана
на нагрузку р=12q, кН, на 1 м высоты, приложенную в плоскости стены,
где q - расчетная ветровая нагрузка на 1 м2 наружной стены; при
одинаковой жесткости поперечных стен принятое значение р соответствует участку
наружной стены шириной 12 м.
Здание проектируется для
городского строительства в I ветровом районе СССР.
Согласно СНиП 2.01.07-85
нормальная ветровая нагрузка определяется по формуле
wm=w0kc, (1)
Черт. 23. Поперечная стена
а – фасад; б – план (размеры в скобках относятся к стенам пяти верхних
этажей)
где w0 - скоростной напор ветра на
высоте 10 м над поверхностью земли, в I ветровом районе СССР; w0=0,27 кПа;
k -
коэффициент, учитывающий изменение скоростного напора по высоте; значения
коэффициентов k приведены в табл.6 СНиП 2.01.07-85. Эти коэффициенты принимаем
для местности типа Б, к которому относятся также здания, расположенные в
городах;
с - аэродинамический
коэффициент.
При одновременном действии
ветра на наветренную и подветренную стены здания коэффициент с=0,8+0,6=1,4.
Коэффициент перегрузки равен 1,2.
Таким образом, расчетная
ветровая нагрузка w на 1 м2 наружных стен здания равна
q=l,2wm=1,2×1,4×0,27k=0,453k кПа
Расчетная нагрузка на 1 м
высоты поперечной стены равна
р=p0k=12w=12×0,453k=5,44k, кН/м, (2)
где р0=5,44 кН/м.
Поперечная стена состоит из
трех вертикальных участков, распределение ветровой нагрузки между этими
участками согласно п. 7.9 может
определяться по формуле
где рi -
нагрузка на i-й участок стены;
dj - прогиб рассчитываемого j-го
участка стены при единичной распределенной нагрузке в уровне 2/3 высоты стены;
di - то же, для участка стены i.
Так как отношения между
прогибами вертикальных участков стены почти не зависят от характера
распределения ветровой нагрузки по высоте стены, определяем эти прогибы при
равномерно распределенной горизонтальной нагрузке. Прогибы должны быть
вычислены на уровне
![]() м.
м.
В табл. 18 приведены характеристики сечений трех
вертикальных участков стены, вычисленные в соответствии с размерами этих
сечений, указанными на черт. 23.
Моменты инерции и положение
центров тяжести тавровых сечений (участки № 1 и 3) определены с помощью
графиков прил. 5, а для более
сложных сечений - по известным формулам сопротивления материалов.
Стена имеет уступ на высоте H1=21,6 м и поэтому может рассматриваться
как стойка переменного сечения (с одним уступом). Очевидно, однако, что на
уровне 26 м изменение сечения почти не отразится на величине прогибов, а тем
более на соотношениях между прогибами вертикальных участков стен. Поэтому,
пренебрегая этим изменением и принимая, в данном случае, сечения нижних этажей,
определяем прогибы dm
от действия изгибающих моментов на уровне 2/3 Н по формуле, приведенной в примере 11:
![]() , (4)
, (4)
где ![]() (5)
(5)
По- этой формуле (размеры в
м):
![]()
![]()
![]()
По методическим соображениям
определяем прогибы dm
так же, как для стойки с одним изменением сечения. Они могут быть вычислены по формуле (6), которая приведена здесь
без вывода. Эта формула может быть применена во всех случаях при расчете
одноступенчатых стоек на равномерно распределенную ветровую нагрузку p:
|
Номер участка |
Этажи |
Высота сечения h, м |
Площадь сечения A, м2 |
Момент инерции I, м4 |
Расстояние центра тяжести
от края (см. черт. 23), м |
|
К |
|
|
левого yb |
правого yr |
|||||||
|
1 |
Нижние |
5,17 |
3,72 |
9,84 |
1,92 |
3,25 |
7,3 |
1,6 |
|
|
Верхние |
- |
2,88 |
7,75 |
1,81 |
3,36 |
- |
- |
|
2 |
Нижние |
2,04 |
2,37 |
0,437 |
0,88 |
1,16 |
1,9 |
- |
|
|
Верхние |
2,04 |
1,82 |
0,313 |
0,88 |
1,16 |
- |
- |
|
3 |
Нижние |
4,80 |
2,70 |
5,65 |
2,57 |
2,23 |
7,9 |
1,2 |
|
|
Верхние |
4,80 |
2,08 |
4,50 |
2,66 |
2,14 |
- |
- |
здесь I1 и I2 - моменты инерции сечений
стен нижних и верхних этажей.
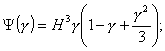 (9)
(9)
![]()
Вычисляем прогибы по формулам (6) - (10) при
![]()
Величины Ф(z),
Y(g) и Ф(g)
одинаковы для всех трех участков здания.
 ;
;
 ;
;
 .
.
По формуле (7)
![]()
По формуле (83)
![]() (размеры в м).
(размеры в м).
Участок 2: I1=0,437 м4; I2=0,312 м4; ![]() ;
;
![]() м4;
м4;
dm2=0,5D(3,2×0,14-0,91×0,1×0,3-0,91×0,109)=0,16D.
Участок 3: I1=5,65 м4; I2=4,5 м4; ![]() ;
;
![]() ;
;
dm3=0,5D(0,22×0,14-0,043×0,1×0,307+0,043×0,109)=0,0124D.
Полученные
величины прогибов совпадают с приведенными выше, вычисленными без учета
изменения сечения стены.
При определении величины
прогибов участков стен 1 и 3 следует учитывать действие поперечных сил, так как
для этих участков H/h<10. Коэффициенты К,
учитывающие влияние распределения касательных напряжений на деформации
изгибаемого элемента, вычислены так же, как и в примере 11, и приведены в табл. 18.
Перемещения dQ определяем по формуле, приведенной в примере 11.
При ![]()
![]() (м).
(м).
Участок 1: A=3,72 м2; K=1,6;
![]()
Участок 3: А=2,7 м2;
К=1,2;
![]()
Полные прогибы
d=dm+dQ
равны:
d1=(0,0071+0,00033)D=0,007431D;
d2=0,l6D;
d3=(0,0124+0,00034)D=0,0127D.
По формуле (3) находим распределение нагрузки между тремя
участками стены:
![]()
![]()
![]()
![]()
Моменты распределяются между
участками стен пропорционально распределению нагрузок
M1=0,614М; M2=0,028М; М3=0,358М.
В качестве примера определим
моменты в нижнем сечении стены.
Нагрузки (скоростные напоры
ветра) разрешается принимать равномерными в пределах зон, не превышающих 10 м.
Принимаем эти зоны равными высоте двух этажей (т. е. около 5,6 м);
равнодействующие этих нагрузок приложены в уровне соответствующих перекрытий.
Величины и положение нагрузок
показаны на черт. 24, где указаны также
значения k, высота а каждой зоны и уровни приложения
сосредоточенных сил.
Черт. 24. Схема нагрузок
Момент в нижнем сечении равен
М=р(5,56×35,6+5,88×30+5,25×24,4+4,66×18,8+4,04×13,2+3,64×7,6+3,12×2)=6820р, кН×м.
При указанном выше [см. формулу (2)]:
р0=5,44 кН/м;
М=682×5,44=3710 кН×м.
Моменты в нижних сечениях
участков стены:
M1=0,614×3710=2280 кН×м;
М2=0,028×3710=110 кН×м;
М3=0,358×3710=1330 кН×м.
Пользуясь данными,
приведенными в табл. 18, и полученными
величинами моментов, определяем напряжения сжатия в нижнем сечении стены,
вызванные ветровой нагрузкой, с целью показать существенное значение этих
напряжений в общем напряженном состоянии стены. Напряжения определяем для
упругой стадии работы кладки по формуле сопротивления материалов
![]() .
.
Участок 1. Максимальное напряжение
сжатия будет у правого края сечения при давлении ветра слева
![]() МПа.
МПа.
Участок 2. Максимальное напряжение
также при давлении ветра слева
![]() МПа.
МПа.
Участок 3. Максимальное напряжение
при давлении ветра справа
![]() МПа.
МПа.
Если кладка выполнена в нижних
этажах из кирпича марки 150 и раствора марки 100, ее расчетное сопротивление
равно R=2,1 МПа. Таким образом, напряжения от ветровой нагрузки составляют в
наиболее жестком участке стены около 35%, а в наименее жестком - около 12%
расчетного сопротивления.
В предельном состоянии, когда
кладка работает в упругопластической стадии, эксцентриситет, создаваемый
ветровой нагрузкой, несколько меньше влияет на несущую способность стены.
СТЕНЫ ИЗ КИРПИЧА, КАМНЕЙ,
КИРПИЧНЫХ ПАНЕЛЕЙ И КРУПНЫХ БЛОКОВ
7.28. Выбор типов наружных и
внутренних стен каменных зданий производится с учетом климатических условий
района строительства, наличия местных каменных материалов: кирпича, пустотелых
керамических и бетонных камней, природных камней, кирпичных панелей и крупных
блоков, теплоизоляционных материалов, а также температурно-влажностного режима
помещений.
7.29. По структуре стены
разделяются: на стены из сплошной кладки из одного какого-либо вида каменного
материала; многослойные, состоящие из двух или более слоев, выполненных из
одного или разных материалов и из облегченной кладки, в которой часть основного
несущего материала заменяется воздушной прослойкой, теплоизоляционными плитами,
камнями из легких и ячеистых бетонов, минеральными засыпками и т. п.
7.30. Наружные стены зданий,
возводимые в различных районах СССР, помимо прочности, удовлетворяющей
требованиям СНиП II-22-81, должны также отвечать требованиям СНиП II-3-79 в
отношении сопротивления теплопередаче, теплоустойчивости, сопротивления
воздухопроницаемости и влажностного режима, а также климатических условий
района строительства.
7.31. Камни и
блоки из ячеистых бетонов применяются в несущих стенах зданий высотой 5 этажей
и менее и в самонесущих стенах в зданиях высотой до 9 этажей.
7.32. Для размещения дымовых
и вентиляционных каналов рекомендуется проектировать местные утолщения стен или
применять специальные бетонные блоки. Внутренние стены и перегородки должны
удовлетворять требованиям прочности, а также защищать от шума в соответствии с
требованиями СНиП II-12-77.
7.33. Легкие каменные
материалы и облегченные кладки рекомендуется использовать, как правило, для
ограждения помещений сухих и с нормальной влажностью воздуха.
Наружные стены помещений с
мокрым режимом эксплуатации следует проектировать из кирпича глиняного
полнотелого пластического прессования или из сплошных камней из бетона (за
исключением бетонов на топливных шлаках) с объемной массой g>1800
кг/м3.
Необходимость устройства
пароизоляции и требуемое сопротивление паропроницанию стен с влажным и мокрым
режимами помещений должны устанавливаться по указаниям СНиП II-3-79.
7.34. Стены из
ячеистобетонных крупных блоков и камней допускается применять в ограждающих
конструкциях зданий с предполагаемым сроком службы 50 и 25 лет. При этом
стеновые блоки и панели изготовляются из ячеистых бетонов проектной марки по
прочности на сжатие не ниже 25.
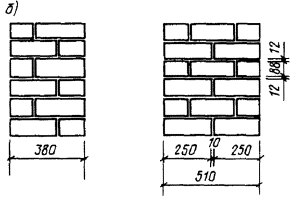

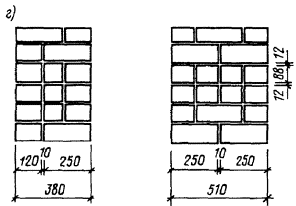
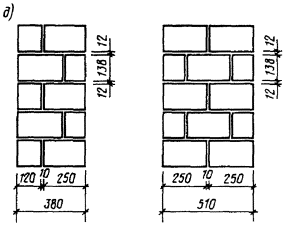
Черт. 25. Кладка из кирпича и
керамических камней
а - цепная перевязка кладки из кирпича толщиной 65 мм; б - то же, из кирпича толщиной 88 мм; в - многорядная перевязка кладки из кирпича толщиной 65 мм; г - то же, из кирпича толщиной 88 мм; д - из пустотелых керамических камней
7.35. Ограждающие конструкции зданий из ячеистобетонных крупных блоков и камней допускаются:
из цементного газобетона и
пенобетона - при сухом, нормальном и влажном режимах помещений; при этом марка
бетона по морозостойкости должна быть не ниже 35;
из других видов ячеистых
бетонов - при сухом и нормальном режимах помещений; при этом марка бетона по
морозостойкости должна быть не ниже 25.
В зданиях с влажным режимом
помещений в случае необходимости на основе теплотехнического расчета следует
предусматривать устройство внутренней пароизоляции стен, а также конструктивные
меры, обеспечивающие сохранение расчетной установившейся влажности стен из ячеистобетонных
блоков или камней на весь период эксплуатации зданий.
Для этой цели рекомендуется
проектировать стены двухслойными: с внутренним слоем из плотных материалов и
наружным - из ячеистобетонных блоков или камней.
7.36. В Северной
строительно-климатической зоне не допускается применять для наружных стен
изделия из крупнопористого бетона, грунтобетонные и сырцовые материалы. В
первой и второй подзонах Северной строительно-климатической зоны наружные стены
должны быть защищены от продувания с внутренней стороны известковой или
цементно-песчаной штукатуркой.
7.37. Сплошная кирпичная
кладка может выполняться по многорядной или однорядной системе перевязки (черт. 25). В летних условиях, а также в
зимних условиях при производстве работ с химическими добавками в растворе рекомендуется выполнять
кладку с многорядной системой перевязки, требующую меньших затрат труда.

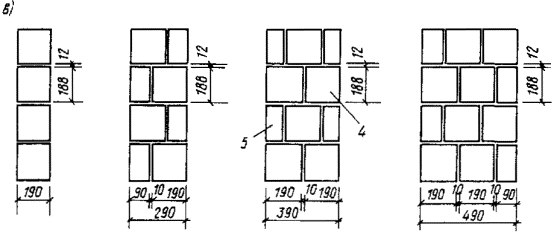
Черт. 26. Кладка из бетонных
или природных камней
а - кладка из
целых камней; б - то же, с перевязкой продольными половинками; в - то же, из
камней со щелевидными пустотами; 1 - тычковый камень; 2 - ложковый камень; 3 -
сплошная продольная половинка; 4 - целый камень; 5 - продольные половинки камня
Кладку стен, выполняемую на обычных растворах методом замораживания, следует производить с однорядной перевязкой.
7.38. Кладка из сплошных и
пустотелых бетонных или природных камней (черт.
26) перевязывается, как правило, тычковыми рядами. Тычковые ряды могут выполняться
также из сплошных продольных половинок.
Перевязка кладки из
пустотелых камней с щелевидными пустотами осуществляется чередованием целых
камней и продольных половинок (см. черт. 26).
Кладка их этих камней при отсутствии продольных половинок может выполняться
только из целых камней с перевязкой тычковыми рядами через два ложковых ряда
(см. черт. 26, а).
7.39. Перевязка кладки из
ячеистобетонных камней в зависимости от размеров камней может выполняться в
один камень или чередованием в рядах целых камней и продольных половинок (черт. 27).
7.40. При необходимости повышения термического сопротивления кирпичных стен сплошной кладки с многорядной перевязкой допускается выполнение кладки с уширенным швом шириной не более 50 мм (черт. 28). Уширенный шов заполняется теплоизоляционным материалом.

Черт. 27. Кладка из
ячеисто-бетонных камней
а - стены толщиной
в 1 камень; б - стены с перевязкой чередованием целых камней и продольных
половинок; 1 - продольная половинка; 2 - целый камень

Черт. 28. Кладка с уширенным
швом
а - кирпичная кладка; б - из
бетонных камней с щелевидными пустотами, 1 - кирпичная кладка; 2 - уширенный
шов, заполненный теплоизоляционным материалом или раствором; 3 - целый камень;
4 - продольная половинка
Кладка из бетонных камней
также может выполняться с уширенным швом шириной не более 40 мм.
Перевязки кладок стен, простенков, столбов, карнизов, каналов и других элементов из кирпича и керамических камней приведены в серии 2.130-1 «Детали стен и перегородок жилых зданий», вып. 1 – «Кирпичные стены сплошной кладки».
НАРУЖНЫЕ КИРПИЧНЫЕ И КАМЕННЫЕ
СТЕНЫ ОБЛЕГЧЕННОЙ КЛАДКИ
7.41. В соответствии с п.
[1.2] в наружных стенах зданий наряду с кладкой из пустотелого кирпича и камней
следует применять облегченную кладку с эффективными плитными утеплителями или
минеральными засыпками.
7.42. Применение наружных
кирпичных стен облегченной кладки с эффективными плитными утеплителями или
минеральными засыпками повышает термическое сопротивление стен, что позволяет
уменьшить расход топлива на отопление зданий. Требуемая толщина кирпичных слоев
в наружных стенах облегченной кладки определяется в основном только из условия
прочности, что позволяет резко сократить в них расход кирпича и цемента по
сравнению с расходом этих материалов в стенах из сплошной кирпичной кладки. При
применении облегченных кладок наибольшая эффективность их достигается в зданиях
с поперечными внутренними несущими стенами и наружными самонесущими стенами
облегченной кладки. По сравнению со зданиями, наружные стены которых выполнены
из сплошной кирпичной кладки толщиной 51-55 см, общий расход кирпича и цемента
при наружных стенах облегченной кладки уменьшается на 25%.
Применение наружных стен
облегченной кладки при строительстве зданий в северных районах с температурами
ниже минус 40°С позволяет еще больше сократить расход кирпича и цемента. В этих
районах для повышения тепловой инерции наружных стен рекомендуется выполнять
внутренний слой кладки толщиной в кирпич.
7.43. Наружные стены
облегченной кладки следует, как правило, применять в зданиях с сухим и
нормальным влажностным режимом помещений. Допускается применение облегченных
кладок в помещениях с влажным режимом при условии защиты внутренней поверхности
стен пароизоляционным слоем. Влажностный режим помещений и сопротивление стен
паропроницанию при этом следует определять по СНиП II-3-79. Применение
облегченных кладок для стен помещений с мокрым режимом не допускается.
7.44. Основным руководящим
документом по проектированию стен облегченной кладки является Серия 2.130-1
«Детали стен и перегородок жилых зданий», вып. 23 – «Наружные кирпичные и
каменные стены облегченной кладки».
7.45. В вып. 23 включены
четыре типа стен облегченной кладки (чертежи 29-32). Кладка типа А (см. черт.
29) состоит из двух кирпичных слоев толщиной в полкирпича, между которыми вплотную к внутренней стенке
устанавливается плитный утеплитель (жесткие и полужесткие минераловатные,
полимерные и другие теплоизоляционные плиты). Если при расчете стены по несущей
способности потребуется увеличение ее толщины, то толщина внутреннего слоя
может быть увеличена до 1-2 кирпичей.
Требуемая толщина штатных
утеплителей определяется по СНиП II-3-79 или по таблицам,
приведенным в указанной выше серии.
Связь между кирпичными
стенками обеспечивается вертикальными поперечными кирпичными диафрагмами
шириной в полкирпича, расстояние между которыми не должно превышать 1,2 м, см.
п. [6.30]. Жесткие связи между слоями обеспечивают их совместную работу. Для
уменьшения влияния „мостиков холода" в диафрагмах имеются воздушные
прослойки, расположенные в шахматном порядке (см. черт. 29). Ширина прослойки между кирпичными слоями
составляет 160 мм, что обеспечивает возможность установки в нее любых
эффективных плитных утеплителей. Между утеплителем и наружным кирпичным слоем
должен быть оставлен зазор шириной не менее 20 мм, предохраняющий утеплитель от
увлажнения атмосферными осадками, которые при недостаточно тщательном
заполнении раствором швов кладки могут проникать через наружный слой.
Закрепление плит утеплителя в проектном положении производится путем установки
полос, нарезаемых из материала утеплителя, в промежутке между утеплителем и
наружным слоем кладки.
Черт. 29. Облегченная кладка
типа А
1 - кирпич; 2 - плитный
утеплитель; 3 - воздушные прослойки
Черт. 30. Облегченная кладка
типа Б
1 - минеральная засыпка; 2 -
поперечные вертикальные диафрагмы
В кладке типа А плиты
утеплителя должны плотно примыкать друг к другу и к кладке поперечных диафрагм.
7.46. Кладка типа Б так же, как и
кладка типа А, выполняется в виде двух кирпичных слоев толщиной в полкирпича,
соединенных вертикальными кирпичными диафрагмами, расстояние между которыми не
должно превышать 1,2 м. Ширина прослойки между кирпичными слоями, заполняемой
минеральными связанными засылками, составляет 270 или 400 мм.
Кладка типа Б применяется для
малоэтажных зданий, строящихся преимущественно в сельской местности. Если для
засыпки применяется керамзитовый гравий объемной массой не более 600 кг/м3,
то высота зданий, наружные стены которых выполняются из кладки типа Б, может
быть увеличена до четырех этажей.
7.47. Расчет стен типов А и
Б, в которых продольные кирпичные слои соединены жесткими связями, см. п.
[6.30], производится как расчет цельного двутаврового сечения.
7.48. Кладку стен типов А и Б
следует выполнять на растворах марки не ниже 50.
7.49. В кладках типов А и Б
для опирания плит утеплителя или засыпок в каждом этаже, в уровне перекрытий,
из внутреннего и наружного слоев выпускаются два ряда тычковых кирпичей,
ограничивающие возможные осадки плит утеплителя или засыпок в пределах одного
этажа.
7.50. Облегченные наружные
кирпичные стены следует применять в зданиях как с поперечными, так и
продольными несущими стенами. Применение облегченных кладок типа А в зданиях с
продольными несущими стенами, в связи с необходимостью утолщения по расчету
внутреннего слоя кладки, вызывает увеличение расхода кирпича и цемента в
наружных стенах.
7.51. Кладка типа В (черт. 31) состоит из наружной кирпичной
стены, толщина которой определяется расчетом по несущей способности, и
примыкающего к ней с внутренней стороны слоя из жестких теплоизоляционных плит
(плиты из ячеистого бетона, фибролита, древесноволокнистые плиты и т.п.). Плиты
утеплителя устанавливаются на гипсовых маяках с образованием воздушной
прослойки между стеной и утеплителем шириной не менее 20 мм. При устройстве
воздушной прослойки водяные пары, проникающие из помещения сквозь утеплитель в
холодное время года, конденсируются на внутренней поверхности кирпичной кладки
и не накапливаются в утеплителе.
Черт. 31. Облегченная кладка
типа В
а - с опорой плит утеплителя на выступающие горизонтальные ряды кирпичной кладки и креплением их на гипсовых маяках; б - с креплением плит на металлических кляммерах и гипсовых маяках; 1 - гипсовый раствор; 2 - гипсовые маяки; 3 - плита утеплителя; 4 - воздушная прослойка; 5 - кляммер; 6 - толщина, принимаемая по расчету
В кладке типа В крепление
теплоизоляционных плит предусматривается двумя способами: с опиранием плит на
выступающие горизонтальные ряды кирпичной кладки или с креплением плит на металлических
кляммерах, забиваемых в швы кирпичной кладки.
7.52. Кладка типа Г (черт. 32) выполняется из легкобетонных или
ячеистобетонных камней марки не ниже 25 с наружной облицовкой толщиной в
полкирпича. Соединение облицовки с кладкой обеспечивается прокладными
кирпичными рядами. В кладке типа Г совмещаются несущие и теплоизоляционные
функции стены. С учетом размеров камней для кладки типа Г приняты две толщины
стен: 420 и 520 мм. Кладка типа Г применяется для зданий высотой до 5 этажей
включ.
Черт. 32. Облегченная кладка
типа Г
1 - прокладные ряды; 2 - кирпичная облицовка; 3 - воздушная прослойка; 4 - камни из легкого или ячеистого бетона
Расчет кладки типа Г
производится по указаниям, приведенным в п. [4.23], как многослойной стены с
жесткими связями.
7.53. Для предотвращения
увлажнения утеплителя атмосферными осадками все швы наружного слоя стен
облегченной кладки необходимо тщательно заполнить раствором и расшить.
Теплоизоляционный слой должен
быть защищен от увлажнения по периметру оконных, дверных и других проемов
устройством сливов, защитных козырьков и т. п.
В процессе производства работ
в период выпадания атмосферных осадков и при перерывах в работе верхнюю
поверхность кладки следует накрывать толем, рубероидом и т. п.
7.54. В углах зданий с
наружными стенами облегченной кладки и в местах примыканий продольных стен к
поперечным в уровне перекрытий следует устанавливать арматурные связи в виде
сварных сеток из проволоки диаметром 3-4 мм класса Вр-1. Связи устанавливаются
в горизонтальных швах кладки в уровне перекрытий.
7.55. Во всех случаях
необходима проверка наружных стен облегченной кладки на воздухопроницаемость в
соответствии со СНиП II-3-79. Для обеспечения требуемого сопротивления стен
воздухопроницанию внутреннюю поверхность их следует покрывать известковой
штукатуркой. В климатических подрайонах 1Б и 1Г, в случаях, когда известковая
штукатурка не обеспечивает требуемого сопротивления стен воздухопроницанию,
внутреннюю поверхность стен следует оштукатуривать цементно-песчаным раствором.
СТЕНЫ ИЗ КИРПИЧНЫХ И КЕРАМИЧЕСКИХ ПАНЕЛЕЙ
7.56. При проектировании
кирпичных и керамических панелей по ГОСТ
24594-81 следует учитывать указания, приведенные в пп. [6.21-6.27].
7.57. Панели из кирпича и
керамических камней подразделяются:
по назначению - для наружных
и внутренних стен (черт. 33-35), а также для перегородок (черт. 36, 37). Конструктивные узлы панелей приведены на черт.38;
по виду воспринимаемых
нагрузок - на несущие и самонесущие, в том числе навесные;
по конструкции - на
однослойные и многослойные;
по виду разрезки - на
однорядные, двухрядные и многорядные;
по месту расположения - на
рядовые, простеночные, торцевые, угловые, парапетные и другие.
7.58. Многослойные панели
наружных стен по конструкции связей между слоями подразделяются:
на связи с соединениями из
сварных каркасов или одиночных стержней (гибкие связи);
на связи с соединениями из
арматурных ребер или отдельных шпонок из раствора или бетона, а также из
кирпича или кирпичной кладки.
7.59. Размеры панелей для
наружных стен жилых, общественных и производственных зданий следует назначать
применительно:
к однорядной разрезке длиной
на один или два планировочных шага;
к вертикальной разрезке
высотой на один или два этажа.
При многорядной разрезке
длина панелей определяется грузоподъемностью монтажного и транспортного
оборудования.
7.60. Размеры
панелей стен и перегородок производственных зданий по длине и высоте в целях
взаимозаменяемости следует назначать в соответствии с размерами бетонных
панелей.
7.61. Размеры панелей
внутренних стен жилых и общественных зданий рекомендуется назначать:
высоту - в соответствии с
высотой этажа;
длину - в соответствии с
планировочным шагом;
толщину - в соответствии с
требованиями прочности и звукоизоляции.
7.62. Размеры дверных и
оконных проемов назначают в соответствии с требованиями государственных
стандартов на эти изделия.
7.63. Для изготовления
панелей следует применять:
кирпич глиняный и керамические
камни, кирпич силикатный, кирпич и камни керамические лицевые;
Черт. 33. Наружная стеновая
панель
1 - арматурный
каркас; 2 - растворный слой; 3 - монтажная петля; 4 - кирпич; 5 - плитный
утеплитель
цементно-песчаный раствор с
добавками, улучшающими его свойства;
теплоизоляционные материалы
для наружных стен в виде жестких и полужестких плит и блоков средней плотности
не более 400 кг/м3, слои теплоизоляционных материалов, в том числе
из бетонов на пористых заполнителях;
металлические изделия в виде
сварных сеток, одиночных стержней, закладных деталей, подъемных петель и
арматурных выпусков.
Кирпич, камня,
теплоизоляционные и отделочные материалы, применяемые для изготовления панелей
наружных стен, должны удовлетворять требованиям по морозостойкости,
предъявляемым к конструкциям с учетом условий их эксплуатации, о чем должна
быть сделана запись в рабочих чертежах.
7.64. Кирпич или керамические
камни, применяемые для изготовления панелей, должны быть марки не ниже 75, а
растворы - марки не ниже 50. Расчетные сопротивления виброкирпичной кладки
приведены в п. [3.2].
7.65. Для приготовления
растворов рекомендуется применять портландцемент (допускается также
шлакопортландцемент). К цементно-песчаным растворам следует добавлять
пластификаторы, а также другие добавки, применение которых улучшает свойства
растворов.
7.66. Для
фасадных поверхностей панелей наружных стен рекомендуется применять лицевые
кирпич и камни, плитки керамические и стеклянные, раствор на белом
портландцементе или растворы с добавлением крошки горных пород. Допускается
также применять другие материалы, морозостойкость которых должна быть не ниже
Мрз 25.
7.67. Сварные сетки и
одиночные стержни для армирования панелей следует изготовлять из стали
следующих видов, классов и марок:
продольные стержни каркасов -
из горячекатаной арматурной стали круглого или периодического профиля классов A-I, А-II, А-III;
сетки и поперечные стержни
каркасов - из холоднотянутой проволоки класса Вр-1;
закладные
детали и соединительные накладки - из горячекатаной полосовой и фасонной стали
марки ВСт3кп2;
монтажные петли - из горячекатаной арматуры стали класса A-I марки ВСт3сп2 или ВСт3пс2 и класса А-П марки 10ГТ.
Изготовление монтажных петель для конструкций,
применяемых при температуре ниже минус 40°С, из стали марки ВСтЗпс2
запрещается.
Черт. 34. Наружная стеновая
панель
1 - гибкая связь;
2 - монтажная петля; 5 - арматурный каркас; 4 - растворный спой; 5 - кирпич; 6
- плитный утеплитель; 7 - накладка, привариваемая электродуговой сваркой
Черт. 35. Виброкирпичная перегородка
1 - закладная деталь; 2 -
монтажная петля; 3 - арматурный каркас; 4 - растворный слой; 5 - кирпич
Черт. 36. Виброкирпичная
перегородка
1 - монтажная петля; 2 -
арматурный каркас; 3 - кирпич; 4 - растворный слой
Черт. 37. Панель виброкирпичной
перегородки
1 - монтажная петля: 2 -
арматурный каркас; 3 - кирпич; 4 - растворный слой
Черт. 38. Конструктивные узлы
а - горизонтальный стык
наружной стеновой панели с плитой перекрытия; б – горизонтальный стык
внутренней стеновой панели с плитой перекрытия; в - вертикальный стык наружных
и внутренних стеновых панелей; г - крепление виброкирпичной перегородки к
железобетонной колонне; 1 - кирпич; 2 - растворный слой; 3 - арматурный каркас;
4 - железобетонная плита; 5 - плитный утеплитель; 6 - внутренняя стеновая
панель; 7 - железобетонная колонна; 8 - монтажная деталь; 9 - виброкирпичная
перегородка
7.68. Если теплоизоляционный
слой панели образован из двух слоев плит эффективного утеплителя, то они должны
быть уложены со смещением швов на величину не менее толщины этих плит.
7.69. Теплоизоляционный слой
необходимо защищать от увлажнения при изготовлении панелей, а также в течение
всего времени строительства и эксплуатации здания.
Паропроницание
конструктивного слоя, наружного по отношению к теплоизоляционному слою, должно
быть больше соответствующего показателя второго конструктивного слоя, включая
пароизоляционный слой.
7.70. В панелях длиной до 6 м
рекомендуется устанавливать две подъемные петли, в панелях длиной более 6 м -
четыре. Диаметр стержней подъемных петель должен определяться в зависимости от
массы панели, но не должен превышать 16 мм.
7.71. Подъемные петли панелей
рекомендуется проектировать таким образом, чтобы они не выступали из плоскости
элемента и были надежно прикреплены к арматурным каркасам или имели
соответствующую анкеровку.
Допускается изготовление
панелей без монтажных петель при условии их подъема и монтажа захватными
устройствами.
7.72. Поставку панелей
потребителю производят по достижении раствором, применяемым для их изготовления,
отпускной прочности не менее 5 МПа (50 кгс/см2).
7.73. Для качественного
заполнения швов, повышающего сцепление кирпича с раствором, рекомендуется
применять вибрирование или другие способы уплотнения раствора (например,
инъекцию), обеспечивающие монолитность и повышающие прочность кирпичной кладки.
При заполнении раствором швов
между пустотелыми кирпичами или камнями следует принимать меры, препятствующие
проникновению раствора в пустоты. Изготовление панелей из пустотелых
керамических камней рекомендуется производить в вертикальном положении.
7.74. Внешний вид, качество
отделки поверхностей, отклонение размеров и другие параметры должны
соответствовать требованиям ГОСТ
24594-81.
7.75. Панели из кирпича и
керамических камней должны иметь конструктивную или расчетную арматуру в виде
сварных сеток (плоских каркасов) или одиночных стержней, см. п. [6.25].
Минимальный процент
армирования расчетной арматурой должен быть не менее 0,1 (по 0,05% у каждой
поверхности панели).
Расстояние между поперечными
стержнями арматурных каркасов, устанавливаемых конструктивно, должно быть не
более 500 мм и не более 80d, где d -
диаметр поперечного стержня.
7.76. Арматурные каркасы
следует устанавливать в сквозных растворных слоях (ребрах) по периметру панели,
по контуру проемов, а также в горизонтальных и вертикальных уширенных
растворных швах кладки с шагом, не превышающим 1600мм.
7.77. Диаметр арматуры сеток
и растянутой продольной арматуры должен быть не менее 3 мм, сжатой продольной
арматуры - не менее 6 мм.
7.78. Толщина сквозных
растворных ребер (расширенных растворных швов), предназначенных для установки
арматуры в панелях наружных стен (с эффективным утеплителем) должна быть не
более 30 мм. Толщина растворных ребер в панелях внутренних стен (перегородок)
устанавливается исходя из конструктивных требований.
7.79. Защитный слой раствора
для арматуры, устанавливаемой по расчету, должен обеспечивать совместную работу
арматуры и материала конструктивных слоев панели на всех стадиях работы
конструкции, а также защиту арматуры от внешних атмосферных, температурных и
тому подобных воздействий.
7.80. Для арматуры,
устанавливаемой по расчету, толщина защитного слоя раствора, вибрированного или
уплотненного другим способом, должна составлять не менее диаметра стержня и не
менее, мм:
10 - в однослойных панелях
или отдельных конструктивных слоях толщиной до 100 мм включ;
15 - в панелях или слоях
толщиной более 100мм.
7.81. Толщина защитного слоя
вибрированного (уплотненного) раствора для поперечной, распределительной и
конструктивной арматуры должна приниматься не менее диаметра указанной арматуры
и не менее 5 мм.
7.82. Толщина защитного слоя
раствора, не подвергающегося уплотнению при изготовлении панели (ручная кладка
в вертикальном положении), должна быть не менее 10 мм.
7.83. Кирпичные панели
рассчитывают на воздействие расчетных нагрузок (в стадии эксплуатации), а также
на сочетание нормативной ветровой и расчетных величин других нагрузок (стадия
строительства). Кроме того, кирпичные панели и перегородки рассчитывают на
воздействие нагрузок, возникающих при их изготовлении, подъеме и монтаже.
Величины этих нагрузок принимаются по п. [6.2]. Перегородки в стадии эксплуатации
рассчитываются на ветровую нагрузку, равную 0,4w0, где w0 - нормативный скоростной
напор ветра, принимаемый по СНиП 2.01.07-85.
Пример 13. Запроектировать самонесущую
виброкирпичную перегородку (кирпич марки 100, раствор марки 75) одноэтажного
промышленного здания высотой 12 м в Москве. Перегородка монтируется из
виброкирпичных панелей заводского изготовления длиной 6 м, высотой 1,2 м,
толщиной 8 см.
Расчетное сопротивление R
определяем по табл. [3] п. [3.2]: Rk=2,6 МПа.
Горизонтальная (ветровая)
нагрузка на перегородку в соответствии со СНиП 2.01.07-85 равна 0,4w0, где w0 - скоростной напор ветра в
районе строительства (I ветровой) равен 0,27 кПа. Расчетная горизонтальная
нагрузка wcal=0,4×0,27=0,108 кПа. Расчетная
погонная нагрузка w=0,108×1,2=0,13 кН/м.
Рассчитываем одну из панелей,
из которых смонтирована перегородка. За расчетную схему принимаем однопролетную
балку, при этом lcal=5,8 м.
![]() кН/м.
кН/м.
Подбор сечения арматуры
проводим по указаниям п. 3.15 СНиП 2.03.01-84 как для
прямоугольного сечения b=120 см, h=8 см, h0=6,5 см с одиночной
арматурой.
На основании п. 7.75 исходя из минимального процента армирования (не
менее 0,1%) определяем:
![]() см2.
см2.
Из п. [6.25] следует, что
площадь конструктивной арматуры должна быть не менее Аs£0,25´1,2=0,3 см2.
Для армирования панели
необходимо не менее двух каркасов, т. е. четырех стержней.
В соответствия с п. [2.6]
принимаем для армирования панелей сталь класса A-I. Расчетное сопротивление Rs определяем по п. 2.27 и табл. 22 СНиП 2.03.01-84; Rs=210 МПа. Минимальный диаметр арматуры равен 6 мм. Аs=4Æ6=1,13 см2. Из условия (34) СНиП 2.03.01-84 определяем
высоту сжатой зоны:
RsАs=Rredbx;
![]() см
см
а из условия (33) того же
СНиП определяем несущую способность сечения:
М=Rredbх(h0-0,5х)=2,6×120×0,76×6,12=1,4 кН×м>0,5 кН×м
Определяем предельную высоту
перегородки при условии опирания нижней панели на фундамент колонны; длина
опорной площадки равна 14 см. Площадь сечения Aс=14×8=112 см2.
Сопротивление смятия
определяется по формуле [18] п. [4.14] Rc=xR, где 
А - расчетная площадь
смятия.
На основании п. [4.16б]
А=(14+8)8=176 см2; x=1,15; Rc=1,15×2,6=3,0 МПа.
Несущая способность Nc одного опорного сечения равна
Nuc=RcА=3,0×176=53 кН; панели - 106 кН.
Вес панели G, кН, с
коэффициентом перегрузки n=1,1 равен G=lbhgn=60×1,2×0,08×18000×1,1×10-3×11,4.
Опорное сечение нижней
панели, на которую через прокладки опираются вышележащие панели, может
воспринять нагрузку от 106/11,4=9,3 панелей (округляем до 9). Следовательно,
предельная высота перегородки равна 9×1,2=10,8 м.
Панели на высоте 10,8 м от
низа перегородки следует устанавливать на монтажные столики, привариваемые к
закладным деталям колонны. Число панелей, устанавливаемых на один монтажный
столик, необходимо рассчитать.
Определяем арматуру
вертикальных каркасов. Конструктивная арматура Аs=0,25×6,0=1,5 см2; армирование симметричное. Принимаем арматуру
класса Вр-1, диаметром 5 мм.
Каркасы необходимо
устанавливать по торцам, у монтажных петель и два между петлями, соблюдая
требования п. 4.14, т. е. 6 каркасов.
Аs=2,84
см2; Rs=340 МПа. Усилие, воспринимаемое вертикальной
арматурой, равно Nu=АsRs=2,84×340=96,6 кН.
Принятого количества арматуры
достаточно для восприятия массы панели с коэффициентом динамичности при монтаже
kd=1,5.
КОМБИНИРОВАННЫЕ КОНСТРУКЦИИ СТЕН
ИЗ КАМНЕЙ РУЧНОЙ КЛАДКИ И СБОРНЫХ ЭЛЕМЕНТОВ
7.84. Повышение
производительности труда и сокращение сроков строительства являются важнейшими
задачами, оптимальное решение которых может быть выполнено путем
индустриализации строительства. Однако организация выпуска строительной
промышленностью сборных элементов (блоков и панелей) из кирпича связана с
некоторыми трудностями и требует значительного времени и средств.
7.85. Конструктивное решение
комбинированных стен состоит в том, что междуоконные простенки монтируются из
легкобетонных блоков, изготовляемых в заводских условиях или на полигонах.
Сплошные участки наружных стен без проемов и внутренние стены на высоту оконных
простенков также монтируются из блоков.
7.86. Сверх блоков по всему
периметру наружных и внутренних стен здания выполняется кирпичный пояс сплошной
кладки, которая является наиболее простой (погонной) по сравнению с кладкой
простенков. Применение комбинированных стен позволяет уменьшить общую
трудоемкость при возведении здания на 25%, сократить сроки строительства и не
требует дополнительных затрат на освоение.
7.87. Комбинированные
конструкции стен допускаются для зданий высотой до 12 этажей.
7.88. Марки кирпича, раствора
и блоков назначаются как для обычных стен согласно рекомендациям настоящего
Пособия.
7.89. Для обеспечения
совместной работы стен должны быть предусмотрены конструктивные мероприятия,
приведенные в пп. 7.21 и 7.119.
7.90. При проектировании и
строительстве зданий с наружными стенами комбинированной конструкции следует
обеспечивать придание этим зданиям архитектурной выразительности.
СТЕНЫ ИЗ КРУПНЫХ БЛОКОВ
7.91. При проектировании стен
из крупных блоков следует учитывать указания, приведенные в пп.[6.28 и 6.29].
7.92. В зависимости от
материально-технической базы и назначения зданий применяются стены из крупных
блоков, изготовленных из цементных и силикатных тяжелых и легких бетонов, из
ячеистых бетонов, из природного камня (известняка, известняка-ракушечника,
песчаника, туфа). Применяются бетонные блоки сплошные, с технологическими
пустотами и пустотелые.
Крупные блоки рекомендуется
изготовлять из кладки, выполненной в заводских условиях или на полигонах, из
кирпича, керамических камней и природных камней, когда из-за трещиноватости или
малой прочности горной породы из нее не могут быть выпилены блоки крупных
размеров.
7.93. По
технико-экономическим показателям целесообразно применять стены из бетонных или
кирпичных панелей. Применение стен из крупных бетонных блоков целесообразно
только при наличии существующей производственной базы.
7.94. Стены крупноблочных
зданий следует проектировать с учетом:
максимального сокращения
типоразмеров блоков и индивидуальных (не номенклатурных) блоков;
соответствия блоков по массе
и размерам, технологии их изготовления, грузоподъемности и габаритам
транспортных приспособлений, а также условиям перевозки и монтажа блоков;
более полного использования
грузоподъемности кранов при монтаже сборных элементов зданий;
применения типовых сборных
железобетонных конструкций и деталей (фундаментов, панелей и плит перекрытий,
лестничных площадок и маршей, крупнопанельных перегородок и т. п.).
Примечание. При назначении типов стен из
крупных блоков следует также руководствоваться технико-экономическими
соображениями с учетом условий материально-технического обеспечения
строительства.
7.95. При проектировании стен
следует применять блоки, предусмотренные действующими альбомами типовых
конструкций, деталей и изделий для жилых, гражданских и производственных
зданий, утвержденными Госстроем СССР.
7.96. Толщины
стен из крупных блоков принимаются равными 20, 30, 40, 50 и 60 см. Если
позволяют местные климатические условия, целесообразно по экономическим
соображениям применять толщины стен с градацией через 5 см.
7.97. Для сокращения типоразмеров
крупных блоков объемно-планировочные решения зданий должны быть наиболее
простыми по форме.
7.98. Разрезка поля стены на
отдельные блоки производится в соответствии с высотой этажей, размерами оконных
проемов и имеющимися на строительстве подъемными механизмами.
В практике строительства
применяются следующие системы разрезки крупноблочных стен: двухрядная,
двухблочная, трехрядная, четырехрядная и многорядная.
Двухрядная разрезка поля стен
(черт. 39) является основным решением
наружной несущей стены из крупных легкобетонных блоков. Двухблочная (ленточная)
разрезка (черт. 40) применяется при
самонесущих и ненесущих (навесных) наружных стенах.
Трехрядная и четырехрядная
разрезка (см. черт. 39, пунктир)
применяется в несущих и самонесущих наружных и внутренних стенах из силикатных
блоков, блоков из кирпича и природного камня.
Для внутренних стен
применяется также однорядная разрезка.
7.99. Стены из крупных блоков
при двухрядной, трехрядной и многорядной разрезке выполняются с перевязкой
вертикальных швов между блоками в каждом этаже перемычечными или поясными
армированными блоками (см. черт. 39).
Этими же блоками осуществляется перевязка углов здания.
Черт. 39. Фрагмент фасадной
стены из кирпичных блоков при двухрядной разрезке
1 - простеночный блок; 2 -
подоконный блок; 3 – перемычечный блок
Черт. 40. Фрагмент фасадной стены из кирпичных блоков при двухблочной (ленточной) разрезке
7.100. Перемычечные и поясные
блоки крепятся между собой стальными связями, сваренными с закладными деталями
блоков (черт. 41). Поясные и
перемычечные блоки должны укладываться, как правило, по наружным и внутренним
стенам, образуя сплошные поэтажные пояса, обеспечивающие связь внутренних и
наружных стен и их совместную работу.
Черт. 41. Стык перемычечных
(поясных) блоков
1 - сварной шов; 2 - раствор; 3 - расшивка раствором; 4 - закладные детали и связи; 5 - перемычечные (поясные) блоки
7.101. При однорядной или двухблочной ленточной разрезке желательна
укладка поясных блоков по внутренним стенам с заделкой концов (торцов) в
наружных стенах. Если это невозможно, то связь между стенами должна
осуществляться жесткими железобетонными шпонками или сваркой имеющихся в блоках
закладных деталей.
7.102. Все стальные и
закладные детали и связи должны быть защищены от коррозии и утоплены в блок,
чтобы не препятствовать равномерному обжатию растворного шва верхних блоков и
не создавать концентрацию усилий в местах расположения связей.
7.103. Крупные блоки из
природного камня (пильных известняков, туфов) имеют, как правило, размеры,
соответствующие трехрядной и многорядной разрезке, что обусловлено технологией
их изготовления (распиловкой).
7.104. Стены из блоков
природного камня выполняются с перевязкой блоков в углах и сплошных участках
стен на глубину не менее 1/4 высоты блока и не менее 20 см.
7.105. Перемычечные и поясные
блоки выполняют железобетонными или же комплексной конструкции, состоящей из
железобетонного поддона или перемычки Г-образной формы, на которую укладываются
блоки.
7.106. Если плиты перекрытий
не опираются на внутренние стены, то для придания стенам большей жесткости и
монолитности вертикальные швы между блоками внутренних стен не должны совпадать
по этажам или для перевязки швов должны применяться поясные блоки или
специальные железобетонные шпонки. Блоки крепятся друг с другом посредством
сварки закладных деталей.
7.107. Вертикальные стыки по
высоте следует тщательно заполнять бетоном или раствором для того, чтобы
избежать продувания швов и проникновения влаги в помещение; в необходимых
случаях швы должны быть утеплены.
7.108. Поверхность пазов в
стеновых блоках рекомендуется делать с мелким рифлением для лучшего сцепления с
блоком укладываемого в пазы бетона заполнения или раствора; более надежное
заполнение вертикальных стыков может быть осуществлено с помощью вибрирования.
7.109. При стенах толщиной
менее 50 см рекомендуется выполнять вертикальные стыки согласно черт.42.
7.110. Вертикальные швы с
внутренней стороны тщательно проконопачиваются жгутами из просмоленной пакли,
затем закрываются двумя слоями рубероида и утепляются пакетом из
теплоизоляционного материала (битуминизированный войлок, плиты из минеральной
ваты и другие материалы, обернутые толем).
Остальное пространство
заполняется легким бетоном с содержанием цемента не менее 250 кг на 1 м3
бетона.
7.111. Перекрытия укладывают
на стены на раствор, марка которого устанавливается проектом, но должна быть не
ниже 50; блоки вышележащего ряда также укладывают на раствор. Швы между плитами
или настилами перекрытий, а также швы в местах примыкания перекрытий к поперечным
капитальным стенам должны быть тщательно замоноличены цементным раствором или
бетоном марки не ниже 50.
7.112. Пространство между
торцами плит или настилов на средней продольной стене или на поперечных стенах
следует заполнять бетоном марки не ниже марки бетона блоков при одном уровне
верха заделки и верха плит перекрытий.
7.113. Торцы пустотных
настилов перекрытий на опорах необходимо заделывать бетоном. Способ заделки
торцов многопустотных настилов на опорах устанавливается проектом в зависимости
от требований прочности, звукоизоляции и теплотехнических условий. Как правило,
торцы пустотных настилов должны быть заделаны бетоном на заводе при
изготовлении настила (до пропарки).
7.114. Анкеры, связывающие
плиты перекрытий (прогоны) со стенами, размещаются в горизонтальных швах стен
или крепятся с помощью сварки к закладным деталям блоков. Концы элементов
перекрытий, укладываемых на прогонах или на внутренних стенах, следует
соединять между собой стальными связями.
7.115. Для горизонтальных
швов, стен крупноблочных зданий должен применяться раствор марки не ниже 25, а
для вертикальных стыков наружных стен, для повышения их водонепроницаемости -
не ниже 100. Толщина горизонтальных швов должна быть не более 20 мм.
Статический расчет
крупноблочных зданий производится по указаниям пп.
7.6-7.25.
7.116. Расчет крупноблочных
стен на осевое и внецентренное сжатие, изгиб, косое внецентренное сжатие и
местное сжатие производится в соответствии с указаниями разд. [4] при расчетных
характеристиках крупноблочных кладок, приведенных в разд. [3].
7.117. Расчет горизонтальных
платформенных стыков (узлов опирания плит перекрытий на стены из крупных
блоков) в стенах из крупных блоков однорядной разрезки производится по
формулам, принятым для расчета стыков крупнопанельных стен.
Черт. 42. Схема заделки
вертикальных стыков между блоками
а - простеночными
на глухих участках стен; б - простеночными и подоконными; в - простеночным и
блоком внутренней стены; г - внутренних стен; 1 - два слоя рубероида; 2 -
утеплитель, обернутый толем; 3 - легкий бетон; 4 - подоконный блок; 5 -
простеночный блок; 6 - раствор; 7 - блок наружной стены; 8 - блок внутренней
стены; 9 - зачеканка раствором
7.118. Свободные деформации,
определяемые при проектировании соединений примыкающих друг к другу стен
вычисляются по п. 7.19. При этом значения
a1 определяются по формуле
![]() , (96)
, (96)
где a
- по п. [3.21];
v - по п.
[3.23].
7.119. Расчет шпонок или поясных
блоков, соединяющих примыкающие друг к другу стены, должен производиться на
суммарное усилие, вызванное неравномерной загрузкой и разной деформативностью
стен, действием ветра и температурно-влажностными воздействиями.
7.120. При расчете на усилия
от ветровой нагрузки, действующие в плоскости стен, должны учитываться указания
о расчете перемычек над проемами на скалывание и изгиб, приведенные в п. [6.15]
.если прочность поперечных стен с проемами обеспечивается только с учетом
жесткости перемычек.
7.121. Горизонтальные швы
должны быть выполнены с разравниванием раствора под рейку. Блок следует
устанавливать на подкладки (маяки), поверхность которых должна быть на 3-4 мм
ниже верхнего уровня раствора, с тем чтобы обеспечить обжатие раствора и
образование более плотного шва. Подкладки должны удаляться после установки
блока, что необходимо для обжатия раствора и равномерного распределения
напряжений в шве.
СТЕНЫ С ОБЛИЦОВКАМИ
7.122. Расчет стен с облицовкой,
выполняемой одновременно с кладкой, следует производить по несущей способности
(прочности и устойчивости) по правилам расчета многослойных стен пп. [4.21 -
4.29] по площади сечения, приведенного к одному материалу (Ared). Рекомендуется, как правило, приводить сечение к основному несущему
слою, т. е. материалу кладки.
Приведение сечения к одному
материалу следует производить с учетом неполного использования прочности слоев
(облицовки и кладки) при их совместной работе (miRi и mR).
7.123. Коэффициенты
использования прочности кладки и облицовки при их совместной работе (m и mi) зависят от соотношения характеристик их деформативности.
Для основных видов кладок и
облицовок величины m и mi определенные на основании
экспериментальных данных, приведены в табл. [22] и [23].
7.124. При отсутствии
перевязки облицовки с кладкой и соединении слоев только гибкими связями
производится раздельный расчет кладки и облицовки по указаниям пп. [4.22б и
4.25].
7.125. Расчет стен с
прислонной тонкой облицовкой, прикрепляемой к стене на растворе, производится
без учета облицовочного слоя. Надежность крепления облицовки должна
обеспечиваться указаниями, приведенными в пп.
7.152-7.155.
7.126. При необходимости
повышения несущей способности облицованной кладки допускается ее армирование
сетками. Во всех случаях армирования стен (конструктивного или же по расчету)
сетки должны укладываться в пределах всего сечения стены включая облицовку.
7.127. Расчет облицованной
кладки, армированной сетками, производится как и неармированной кладки с
облицовкой по пп. [4.21 - 4.29] и 7.122,
при этом принимается расчетное сопротивление для армированной кладки Rsk - при центральном сжатии и Rskb - при внецентренном.
Величины Rsk и Rskb принимаются не более 1,5R. При
определении j и mg принимается упругая
характеристика ask
для армированной кладки.
В случае армирования сетками
стен, облицованных бетонными плитами, перевязанными с кладкой прокладными
рядами из тех же плит, допускается учитывать в расчете только арматурные сетки,
располагаемые в сечении стены над и под прокладными рядами облицовки.
7.128. В простенках многоэтажных
зданий, облицованных различными видами фасадных материалов, при жестком
соединении слоев во всех этажах, где достигается использование расчетной
несущей способности стены более чем на 90%, следует предусматривать
конструктивное армирование: в швы кладки и облицовки укладываются арматурные
сетки из стали диаметром 3-4 мм с ячейками размером 120´120 мм. Сетки располагаются в каждой трети высоты простенка, но не реже
чем через 1 м.
7.129. При наличии наружных
обрезов в стенах, во избежание отслаивания облицовки, следует укладывать в швы
кладки и облицовки сетки из арматуры диаметром 4-6 мм с ячейками размером не
менее 80´80 мм. Сетки располагаются на
участке кладки, примыкающему к обрезу не менее чем в двух швах через два ряда
кладки по высоте стены, начиная с четвертого шва от обреза.
В местах нависания стен с
облицовкой над цоколем (или фундаментными блоками) должны выполняться следующие
конструктивные мероприятия:
нависание кладки стен не
должно превышать 60мм;
при высоте здания до 9 этажей
в месте нависания над цоколем три ряда кладки стены на всю толщину выполняются
из сплошного кирпича с цепной перевязкой и армированием в первом горизонтальном
шве сеткой из стали диаметром 5-6 мм с ячейками 80´80 мм;
при высоте здания более 9
этажей в месте нависания кладки укладывается железобетонная плита толщиной 8-10
см с армированием сетками из стали диаметром 6-8 мм.
7.130. В
простенках с облицовкой, жестко связанной с кладкой, в многоэтажных зданиях,
возводимых при отрицательных температурах, конструктивное армирование в
соответствии с п. 7.128 является
обязательным во всех этажах, где расчетная несущая способность в законченном
здании используется более чем на 50%. Арматурные сетки следует укладывать в
горизонтальные швы по всей толщине стены под тычковыми (прокладными) рядами,
перевязывающими облицовку с кладкой.
7.131. Во
избежание значительного уменьшения несущей способности стен с облицовками и
связанного с этим утолщения стен при выборе типа облицовки следует
руководствоваться следующими правилами:
при жестком соединении
облицовки с основным материалом стен высота облицовочных изделии без
армирования должна быть не более трех рядов, а при наличии армирования - шести
рядов основной кладки стены;


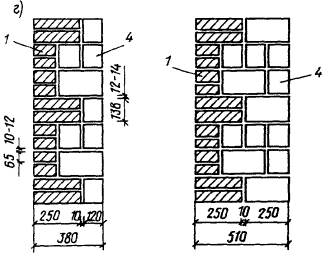
Черт. 43. Облицовка стен
лицевым кирпичом
а, б - из кирпича толщиной 65 мм; в - из кирпича толщиной 88 мм; г - из стеновых керамических камней; 1 - лицевой кирпич; 2 - кирпич рядовой глиняный, силикатный или полусухого прессования толщиной 65 мм; 3 - силикатный толщиной 88 мм; 4 - стеновые керамические камни
марка облицовочного материала
должна быть, как правило, на одну ступень выше марки материала основной кладки
стены;
облицовка должна соединяться
со стеной гибкими связями,
7.132. При облицовке стен
лицевым кирпичом толщиной 65 мм (черт. 43)
перевязка облицовки с кладкой производится по многорядной системе. Тычковые
ряды кирпича толщиной 65 мм, перевязывающие облицовку с кладкой, располагаются:
при полнотелом кирпиче
толщиной 65 мм - 1 тычковый ряд на 6 рядов лицевой кладки и пустотелом - 1
тычковый на 4 ряда лицевой кладки;
при кладке из кирпича
толщиной 88 мм - 1 тычковый ряд на 5 рядов лицевой кладки;
при кладке из керамических
камней высотой 138 мы - 2 тычковых ряда на б рядов лицевой кладки.
Тычковые ряды лицевого
кирпича толщиной - 88 мм, перевязывающие облицовку с кладкой из кирпича
толщиной 65 мм - 1 тычковый ряд на 4 ряда лицевой кладки.
7.133. Лицевая кладка из
керамических камней (черт. 44)
перевязывается с кладкой стены тычковыми рядами камней - 1 ряд на 3 ряда
лицевой кладка.

Черт. 44. Облицовка стен
лицевыми керамическими камнями
а - из кирпича
толщиной 65 мм; б - из лицевых керамических камней, 1 - лицевые керамические
камни; 2 - глиняный, силикатный кирпич толщиной 65 мм; 3 - стеновые керамические
камни
7.134. Рекомендуется, как
правило, производить перевязку лицевого слоя со стеной сплошными тычковыми
рядами.
7.135. Для перевязки лицевого
слоя с кладкой целесообразно изготовлять и применять специальные (полнотелые)
тычковые кирпичи или камни.
7.136. Облицовка Г-образными
бетонными плитами (черт. 45)
производится одновременно с кладкой стены: перевязка осуществляется заделкой в
кладку хвостовой части плиты на глубину не менее 75 мм. Высота плит должна быть
не более 600 мм.
Черт. 45. Облицовка стен
Г-образными закладными бетонными плитами
а - из кирпича толщиной 65 мм; б - из керамических камней; 1 - закладные бетонные плиты; 2 - кладка из кирпича толщиной 65 мм; 3 - кладка из керамических камней высотой 138 мм
7.137. Облицовка из плоских
бетонных плит, производимая одновременно с кладкой стены, перевязывается с
кладкой прокладными рядами из таких же плит, располагаемыми после каждого ряда
плит по высоте фасада. Толщина прокладных рядов плит должна быть равной или
кратной толщине ряда кирпича, глубина заделки прокладного ряда - не менее 120
мм (черт. 46). Толщина плит должна быть
не менее 40 мм, высота не более 300 мм.
Черт. 46. Облицовка стен плоскими бетонными плитами
а - из
кирпича толщиной 65 мм; б - из кирпича толщиной 88 мм; 1 - плоские плиты;
2 - прокладной ряд из плит
7.138. При установке бетонных
плит в процессе кладки с креплением на гибких связях (анкерах) их размеры
определяются исходя из технологических возможностей их изготовления. Толщина
бетонных плит должна быть не менее 40 мм, масса при ручной кладке - не более 40
кг. Для обеспечения необходимой надежности крепления облицовки на гибких связях
в период эксплуатации зданий следует:
для связей применять
коррозионностойкие стали;
в каждом этаже облицовочный
слой опирать на специальную Г-образную армированную плиту, заделанную в кладку
или железобетонный пояс;
под опорной плитой или поясом
оставлять осадочный горизонтальный шов толщиной 20-25 мм, который заполняется
мягкой прокладкой и с наружной стороны расшивается гидроизоляционной мастикой.
7.139. Лицевой кирпич, камни
и облицовочные плиты могут укладываться с перевязанными или неперевязанными по
фасаду вертикальными швами.
7.140. Толщина швов облицовки
из лицевого кирпича или керамических камней принимается той же, что и в
основной кладке стены. Толщина вертикальных швов облицовки из плит
устанавливается в соответствии с архитектурными требованиями. Швы в облицовке
заполняются раствором и расшиваются в процессе кладки стены.
7.141. Для облицовки стен из
бетонных камней может быть применен полнотелый лицевой кирпич (черт. 47). Облицовка лицевым кирпичом
перевязывается с кладкой из бетонных камней тычковыми рядами кирпича - 1
тычковый ряд на 6 рядов кирпича при толщине кирпича 65 мм и 1 тычковый ряд на 5
рядов при кирпиче толщиной 88 мм.
Черт. 47. Облицовка фасадов
стен из бетонных камней
а - с перевязкой прокладными тычковыми рядами кирпича толщиной 65 мм; б - то же, кирпич толщиной 88 мм; 1 - лицевой кирпич; 2 - бетонный камень
7.142. Стены из кирпича и
керамических камней допускается облицовывать природным камнем.
7.143. Основной вид облицовки
из природного камня - пиленая плита или камень. Для наружной облицовки
применяются плиты толщиной 10, 20, 30 и 40 мм (в виде исключения - толщиной 60
мм из более мягких пород).
Наибольший размер сторон плит
не должен превышать 600 мм.
Фактура лицевой поверхности в
зависимости от архитектурных требований может быть пиленая, полированная,
шлифованная, лощеная.
7.144. Технические
характеристики изделий из природного камни, применяемых для наружной облицовки,
должны удовлетворять следующим требованиям:
прочность на сжатие – не
менее 10 МПа (100 кгс/см2);
морозостойкость – не ниже
Мрз25;
коэффициент размягчения – не
менее 0,7.
7.145. Облицовка плитами из
природного камня крепится к стенам зданий следующими способами:
на анкерах и
цементно-песчанном растворе с оставлением горизонтальных компенсационных швов
при толщине плит 20 мм и более;
на цементно-песчанном
растворе (без анкеров) для травертина и других пород с крупными открытыми
порами при толщине плит 10 мм и размере не более 400´200 мм (200 мм – высота), с обязательным устройством швов по контуру
плит для стен высотой не более 5 м
на относе от стены с
разработкой отдельного проекта на крепление плит.
7.146. Горизонтальные
компенсационные швы в облицовке предусматриваются через два этажа по высоте
стены.
Плиты облицовки поля стены
должны крепиться к рабочей арматуре, устанавливаемой в петли-выпуски с помощью
крюков. В горизонтальных швах смежные по вертикали плиты соединяются не менее
чем двумя штырями на плиту (черт. 48).
7.147. При проектировании
крепления облицовки поля стены следует предусматривать (см. черт. 48):
V-образные
петли-выпуски для удержания рабочей арматуры (диаметром 8 мм);
рабочую арматуру (диаметром
10-12 мм);
крюки простые для крепления
элементов облицовки к рабочей арматуре (диаметром 4-6 мм)
штыри и скобы для соединения
смежных элементов облицовки между собой (диаметром 4-6 мм).
Петли-выпуски и рабочая
арматура должны предусматриваться из оцинкованной стали; крюки, штыри и скобы –
из нержавеющей стали марок 12Х13; 12Х18Н10Т (ГОСТ 18143-72).
7.148. Петли-выпуски для
крепления рабочей арматуры укладывают в швы кладки стены в процессе ее
возведения с шагом 0,5 м по горизонтали и вертикали.
7.149. Число крюков (анкеров) принимается: один на площадь поверхности плиты не более 0,12 м2. На каждой плите устанавливается не менее двух крюков. Смежные плиты крепятся между собой штырями - не менее двух на плиту.
7.150. При облицовке плитами
из природного камня устройство швов и конструкция всех выступающих частей
здания должны исключать попадание за облицовку воды.
Для этого необходимо:
горизонтальные
накрывочные камни парапетов, ограждения балконов и другие детали выполнять из
твердых пород. Поверхность верхней грани должна иметь уклон 3-4° или перепад
отметок по вертикали не менее 15 мм. Устройство капельника в накрывочной плите
обязательно, швы между накрывочными камнями тщательно загерметизировать;
все выступающие детали
выполнять из камня твердых пород (карнизы, пояса цоколя и др.) и делать уклон
наружу для стока воды;
в случае выполнения
выступающих деталей из камня средней твердости (мрамора, травертина,
известняка) делать металлические покрытия из меди, цинка или оцинкованного
железа.
7.151.
Облицовка готовых кирпичных стен может быть выполнена керамическими и
стеклянными шляпками с креплением на растворе.
7.152. Применение для облицовки
плоских плиток с креплением их на растворе по готовым кирпичным стенам
допускается только в порядке исключения в зданиях не выше 9 этажей при
выполнении стен из глиняного кирпича пластического прессования и не выше 5
этажей при выполнении стен из силикатного или глиняного кирпича полусухого
прессования. При этом размеры плиток должны быть не больше 250´65 мм, где 65 мм - высота плиток при их укладке по высоте стены.
Крепление на растворе более крупных плиток не допускается.
Черт. 48. Крепление к стене облицовочных плит из природного камня
1 – облицовочная плита; 2 – крюк; 3 – петля, заложенная при кладке
стены; 4 – рабочая арматура (вертикальная и горизонтальная); 5 – штырь; 6 –
скоба для соединения угловых плит.
Прочность раствора для
крепления плиток к кирпичной кладке должна быть не менее 10 МПа (100 кгс/см2).
В виде исключения для стен
зданий из силикатного кирпича высотой до 9 этажей может быть допущена облицовка
плоскими плитками. При этом облицовка должна крепиться на слое раствора,
нанесенного по арматурной сетке, прикрепленной к стене стальными стержнями в
швах кладки.
7.153. Кладка стен,
предназначенных для дальнейшей облицовки плоскими малогабаритными плитками с
креплением их на растворе, должна быть выполнена впустошовку.
7.154. Облицовка готовых стен
плоскими плитами с креплением на растворе или на растворе и анкерах допускается
не ранее чем через 6 мес. подле того, как нагрузка на стены достигнет 85%
полной проектной нагрузки.
7.155. Облицовку готовых стен
плоскими плитами с креплением на растворе и на растворе и анкерах допускается
производить при устойчивой положительной температуре не ниже 6°С или при
условии электропрогрева.
7.156. В случае облицовки
стен Г-образными плитами для облицовки откосов простенков применяются
специальные угловые плиты, дополнительно укрепляемые анкерами. Поверхность
простенка между угловыми плитами облицовывается рядовыми плитами.
7.157. При облицовке стен
плоскими плитами для углов зданий и простенков могут применяться рядовые и
специальные облицовочные угловые плиты.
7.158. Облицовка перемычек
над оконными и дверными проемами при облицовке стен прислонными плитами,
керамическими камнями или лицевым кирпичом производится теми же материалами,
что и стены, а при применении для облицовки закладных плит - плитами
специальной формы и размеров.
7.159. Лицевая кладка цоколя
выше гидроизоляционного слоя может быть выполнена из полнотелого лицевого
кирпича пластического прессования, плит из тяжелого бетона или естественного
камня.
7.160. Ширина кирпичных
простенков, проектируемых с облицовкой, должна быть кратной 1/2 кирпича или
соответствовать размерам элементов облицовки.
7.161.
Производство работ методом замораживания на обыкновенных растворах допускается,
как правило, только для стен высотой не более 4 этажей из глиняного кирпича
пластического прессования с облицовкой лицевым кирпичом и стен из керамических
камней с облицовкой лицевыми керамическими камнями. При применении метода
замораживания по указаниям СНиП II-22-81 снижаются характеристики прочности и
жесткости кладки. Облицовка стен плитами, перевязанными с кладкой прокладными
рядами, или облицовка Г-образными закладными плитами допускается в зимних
условиях только при условии применения растворов с противоморозными добавками.
7.162. Работы по
облицовке производятся в соответствии с проектом, в котором должны быть указаны
раскладка плит и камней, способы крепления угловых, перемычечных плит и
приложена их спецификация. В проекте следует указывать виды кирпича для кладки
стен, рекомендуемые при предусмотренной в проекте облицовке.
Замена на строительстве
одного вида кирпича другим или изменение вида облицовки не допускается без
согласования с проектной организацией.
Рабочие чертежи проекта и
проект организации работ должны содержать указания по возведению стен с
облицовками в зимних условиях, а в случае необходимости - требования к
применению противоморозных добавок в растворах, рекомендации по конструктивному
армированию.
Пример 14. Проверить прочность простенка
из глиняного кирпича пластического прессования с облицовкой из керамических
камней на растворе марки 75.
Расчет простенка по несущей
способности производится в соответствии со СНиП II-22-81.
Данные для расчета:
кирпич марки 100 толщиной 65
мм, Rk=1,7 МПа (17 кгс/см2);
керамический камень марки 125
высотой 138 мм;
R0=1,9 МПа (19 кгс/см2);
раствор марки 75;
высота этажа Н=3000 мм;
ширина простенка b=900 мм;
толщина облицовочного слоя
с=120 мм;
продольная сила в сечении
N=500 кН (50 тc);
изгибающий момент М=20 кН×м (2 тc×м);
коэффициенты использования
прочности слоев в стене из кирпича глиняного пластического прессования
принимаются по табл. [23] и указаниям пп.[4.22-4.24; 4.27]:
для кладки mk=0,8;
для облицовки m0=1,0.
Расчетная несущая способность
Ncc определяется по формуле [13]
Ncc=mgj1mkRkAc,redw
Согласно пп. [4.22а и 4.23]
различную прочность и упругие свойства слоев и неполное использование их
прочности при совместной работе в стене следует учитывать путем приведения
сечения к материалу основного несущего слоя.
Эксцентриситет всех усилий
определяется по отношению к оси приведенного сечения (черт. 49).
Приведенная ширина bred изменяется пропорционально отношению расчетных сопротивлений и
коэффициентов использования слоев по формуле
![]() мм
мм
Площадь приведенного сечения
Ared=bredc+bd=1260×120+900×390=5,0×105 мм2.
По при
л. 5 находим положение центра
тяжести приведенного сечения
![]()
Расстояние центра тяжести
сечения от края полки
z0=ch=0,465×510=237 мм.
Эксцентриситет приложения
усилий ![]() м=40 мм
м=40 мм
Черт. 49. Определение приведенной площади сечения простенка
При эксцентриситете в сторону
полки для таврового сечения расстояние от точки приложения силы до границы
расчетной сжатой зоны х определяется по формуле
е1=z0-е0=237-40=197 мм.
![]() мм.
мм.
Тогда высота сжатой зоны
сечения hс,red=х+е1=228+197=425
мм.
Площадь сжатой зоны
приведенного сечения
Ac,red=bredc+b(hc,red-с)=1260×120+900(425-120)=4,3 105 мм2.
При внецентренном сжатии
коэффициенты продольного изгиба j определяются согласно пп.
[4.2-4.7 и табл. 18] в зависимости от гибкости элемента
![]() при l0=Н=3000 мм по формуле
при l0=Н=3000 мм по формуле
![]() .
.
Радиус инерции сечения определяется
по формулам:
для приведенного сечения 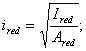
для сжатой зоны 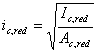 .
.
Момент инерции сечения
определяется по графику прил.5:
при ![]()
Ired=hbredh3=0,071×1260×5103=118,7×108
мм4;
![]() мм4;
мм4;
 мм;
мм;
 мм;
мм;
![]()
Определяем коэффициенты
продольного изгиба
![]()
Расчетная несущая способность
стены определяется по формуле [13].
Так как ired и ic,red>8,7, то коэффициент mg принимается равным 1 исходя
из указаний п. [4.7].
Согласно п. [4.26] при
эксцентриситете в сторону облицовки коэффициент w принимается равным единице.
Ncc=1×0,96×0,8×1,7×4,3×105×1=563 кН.
Расчетная несущая способность
стены с облицовкой Ncc=563 кН больше расчетной продольной силы N=500 кН,
следовательно, стена удовлетворяет требованиям прочности.
СТЕНЫ ПРОИЗВОДСТВЕННЫХ И
СЕЛЬСКОХОЗЯЙСТВЕННЫХ ЗДАНИЙ
7.163. Несущие каменные
конструкции допускается применять при строительстве производственных зданий,
оборудованных кранами грузоподъемностью до 100 кН при наличии машин 1-й
категории динамичности без виброизоляции и 2-й категории при виброизоляции.
Несущие каменные стены и столбы при крановых нагрузках допускается изменять в
зданиях высотой не более 10 м.
7.164. Для
кладки несущих стен и столбов производственных зданий следует применять кирпич
марки не ниже 75 и бетонные или природные камни, как правило, марки не ниже 50.
Для зданий с помещениями I группы (см. примечание к табл. 19) высотой до 4 м
допускается применение природных камней марок не ниже 50.
7.165. Для кладки стен и
столбов производственных зданий следует применять марки раствора не ниже
указанных в табл. 19.
|
Группа помещений |
Минимальные марки
растворов кладки |
|
|
стен |
столбов |
|
|
I |
25 |
50 |
|
II |
50 |
100 |
Примечание. К I группе относятся помещения динамических
нагрузок или же с машинами 1-й категории динамичности. Ко II группе
- помещения с кранами или же с машинами 2-й категории динамичности.
7.166. При опирании на стены или столбы перекрытий, на которых
расположены машины 2-й категории динамичности, а также подкрановых балок,
следует проводить следующие конструктивные мероприятия:
а) применять типы стен из
сплошных кладок;
б) усиливать
участки кладки под опорами перекрытий или балок сетчатым армированием
дополнительно к необходимому по расчету на местное сжатие. Армирование кладки
производится в пределах 1-1,2м ниже опор через 3 ряда кладки сетками с ячейкой
размером 100´100 мм из проволоки диаметром 3-5 мм;
в) устанавливать
дополнительные связи в углах и пересечениях стен в уровне перекрытий из двух
стержней диаметром 8 мм;
г) при кранах
грузоподъемностью более 50 кН усиливать стены армокирпичными поясами, причем
суммарное сечение арматуры в поясе следует принимать не менее 4 см2
при глухих стенах и 6 см2 - при стенах, ослабленных проемами. Пояса
и обвязки располагаются в верхней части сухих стен, а при наличии проемов
совмещаются с перемычками. При наличии мостовых кранов пояса располагаются в
кладке стен на уровне подкрановой балки. В зависимости от интенсивности
динамических воздействий и высоты здания пояса могут располагаться также и в
других уровнях по высоте стены;
д) кирпичные столбы и
пилястры, несущее крановые нагрузки, кроме арматуры, указанной в подп. «б» и
«в», должны быть конструктивно армированы стальными сетками, укладываемыми не
реже чем через 1,5 м по высоте столба или пилястры.
7.167. Под опорами ферм, прогонов и подкрановых
балок для распределения давления должны быть уложены железобетонные плиты,
связывающие пилястры со стенами. Следует также применять другие конструктивные
указания пп. [6.40-6.43].
7.168. Самонесущие стены в каркасных зданиях должны
быть соединены с колоннами гибкими связями, допускающими возможность
независимых вертикальных деформаций стен и колонн (черт. 50).
Черт. 50. Гибкие связи для
крепления самонесущих стен к каркасу.
1 – стержни диаметром 10 мм
7.169. Связи устанавливаются
через 1,2 м по высоте колонн и обеспечивают устойчивость стен, а также передачу
действующей на них ветровой нагрузки на колонны каркаса.
7.170. При крановых нагрузках следует учитывать в расчете понижение
несущей способности кладки при повторяющихся нагрузках уменьшением расчетных
сопротивлений согласно указаниям п. [3.13].
7.171. Стены
сельскохозяйственных зданий и сооружений следует проектировать с учетом
требований СНиП 2.10.01-84, СНиП
2.10.03-84 и СНиП II-108-78.
7.172. Влажностный режим
помещений устанавливается нормами технологического проектирования зданий
различного назначения.
7.173. Каменные стены
сельскохозяйственных зданий выполняются из кирпича, бетонных и природных
камней. В ненесущих стенах одноэтажных зданий с предполагаемым сроком службы 25
лет с нормальным и влажным режимом могут применяться грунтобетонные камни и камни
из сырцовых материалов.
Примечания: 1. Сельскохозяйственные
здания с предполагаемым сроком службы 100 лет, как правило, не проектируются.
2. В зданиях с
влажным режимом с предполагаемым сроком службы 25 лет допускается применение
камней из пено- и газобетона при условии устройства пароизоляции на внутренней
поверхности стены.
7.147. Толщина сплошных стен
и толщина утеплителя в облегченных стенах принимается по теплотехническому
расчету из условий невыпадения конденсата на внутренней поверхности стен. Для наружных
стен сельскохозяйственных зданий с нормальным влажностным режимом рекомендуется
применение облегченной кладки типа Б с минеральными засыпками (см. п. 7.46).
7.175. При
проектировании одноэтажных зданий, стены которых воспринимают горизонтальные
нагрузки (от давления сыпучих материалов или грунта), покрытия могут
рассматриваться как опоры стен, см. п. [6.7, 6.8]. При этом должна быть
обеспечена связь между стеной и покрытием анкерами, сечения которых определяются
расчетом. В этом случае при небольших вертикальных нагрузках от веса покрытия
толщина стен определяется обычно из условия устойчивости (величины
эксцентриситета нормальной силы). При наличии верхней опоры стены рекомендуется
проектировать с пилястрами, расположенными с внутренней стороны. В заглубленных
одноэтажных зданиях, при горизонтальных нагрузках от давления грунта пилястры
следует располагать с наружной стороны. Расстояние между пилястрами (в осях)
рекомендуется принимать равным 2 или 3 м, а толщину стен и ширину пилястр - 25
см (черт. 51). Прочность стен на
участках между пилястрами должна быть проверена на изгиб по перевязанному
сечению при действии горизонтальных нагрузок. При необходимости утепления стен
плитный утеплитель или минеральная засыпка располагаются с наружной стороны
стены и ограждаются защитной стенкой толщиной в полкирпича (12 см),
перевязанной с пилястрами (см. черт. 51).
Черт. 51. Стены, воспринимающие
горизонтальные нагрузки
а - для неутепленных зданий;
б - для утепленных зданий; 1 - кирпичная кладка; 2 - утеплитель
7.176. Кроме влияния
влажности воздуха помещений следует учитывать также агрессивное воздействие
газовой среды сельскохозяйственных зданий на каменные материалы, степень
которого (в том числе складов минеральных удобрений), а также необходимость
защиты и рекомендуемые варианты защитных покрытий принимаются по СНиП
2.03.11-85.
РАСЧЕТ УЗЛОВ ОПИРАНИЯ ЭЛЕМЕНТОВ НА КИРПИЧНУЮ КЛАДКУ
7.177. Расчет узлов опирания
элементов на кирпичную кладку производится по пп. [6.44 - 6.46].
7.178. Прочность кладки в
пределах высоты опорного узла должна быть не меньше прочности остальной части
кладки (например, если кладка ниже или выше перекрытия армирована сетками,
такое же армирование должно применяться в опорном узле).
7.179. При опирании сборных
перекрытий на стены толщиной 25 см и менее из штучных каменных материалов концы
железобетонных настилов или плит на опорах должны быть связаны арматурой и
замоноличены. При отсутствии замоноличивания расчетное сопротивление кладки
опорных участков стен должно быть уменьшено на 20%.
КАРНИЗЫ И ПАРАПЕТЫ
7.180. При проектировании
карнизов и парапетов следует руководствоваться указаниями, приведенными в пп.
[6.54-6.64].
7.181. Для устройства
карнизов с выносами, превышающими половину толщины стены, см. п. [6.57],
применяются железобетонные плиты или балки, закрепляемые при помощи анкеров,
заделываемых в нижних участках кладки, а в зданиях со стенами из кирпичных
панелей и блоков (бетонных и кирпичных) - специальные карнизные блоки.
7.182. При больших выносах
карнизов для уменьшения их веса применяются сборные пустотелые железобетонные
карнизы.
7.183. При расчете стены под
карнизом незаконченного здания (при отсутствии крыши и чердачного перекрытия)
нормативная ветровая нагрузка на внутреннюю сторону стены принимается на уровне
выше соседних стен, см. п. [6.55].
7.184. Если по проекту концы
анкеров заделываются под чердачным перекрытием, то при расчете учитывается
наличие чердачного перекрытия (полностью или частично) и в чертежах должно быть
сделано указание об укладке плит перекрытия до устройства карниза.
ПЕРЕМЫЧКИ
7.185. Для перекрытия проемов
в каменных стенах следует, как правило, применять железобетонные перемычки,
которые рассчитываются как балки на нагрузки, указанные в п. [6.47]. Должна
также проверяться прочность кладки при смятии под опорами перемычек.
7.186. При расчете кладки на смятие
в опорных сечениях перемычку следует рассчитывать как заделанную на опорах по
п. [6.44] при соблюдении условия
М/а<N, (97)
где М - изгибающий момент в
перемычке в зоне заделки;
N - усилие защемления опоры
перемычки, действующее по контакту с кладкой над опорой перемычки, от веса
кладки и других вертикальных нагрузок;
а - глубина заделки
перемычки.
Примечание. При определении усилия N
допускается включать вес кладки и нагрузки от перекрытий за пределами опоры
перемычки, ограниченный углом 40° от вертикали.
7.187. Расчет заделки железобетонных перемычек в кладку производится по п.
[6.46]. При этом эксцентриситет приложения нагрузки относительно середины
заделки определяется по формуле
е0=М/Q, (98)
где Q - опорная реакция перемычки.
Если условие
(98) не соблюдается, то перемычка рассчитывается как свободно лежащая балка и
расчет кладки на смятие под ее опорами, производится по п. 4.15.
7.188. При отсутствии
железобетонных перемычек допускается применение каменных (рядовых, клинчатых и
арочных), проектирование которых производится по указаниям п. 7.189.
7.189. Пролеты неармированных
каменных перемычек при марке кирпича или камня 75 и выше не должны превышать
указанных в табл. 20.
|
Марка раствора |
Максимальные пролеты
перемычек, м |
|||
|
рядовых |
клинчатых |
арочных при высоте подъема |
||
|
1/8-1/12 пролета |
1/5-1/6 пролета |
|||
|
50-100 |
2 |
2 |
3,5 |
4 |
|
25 |
1,75 |
1,75 |
2,5 |
3 |
|
10 |
- |
1,5 |
2 |
2,5 |
|
4 |
- |
1,25 |
1,75 |
2,25 |
Примечания: 1. Максимальные пролеты перемычек
из кирпича, бетонных и природных камней марок 35-50 уменьшаются умножением на
коэффициент 0,8.
2. Арочные перемычки с
пролетами больше указанных в настоящей таблице конструируются и рассчитываются
как арки.
3. Неармированные каменные
перемычки (рядовые, клинчатые и арочные) не допускаются в стенах зданий,
которые будут подвергаться значительным вибрационным или ударным воздействиям,
а также в случаях, когда возможна неравномерная осадка стен.
7.190. Наименьшая конструктивная высота неармированных каменных
перемычек указана в табл.21.
7.191. В рядовых
перемычках во избежание выпадения кирпичей или камней из нижнего ряда под ним
необходимо укладывать слой раствора толщиной 2-3 см и арматуру в количестве не
менее одного стержня сечением 0,2 см2 на каждые 13 см толщины стены.
7.192. Рядовые, клинчатые и
арочные перемычки рассчитываются как арки. При распределении распора расстояние
кривой давления от верха перемычки в замке и от низа перемычки в пятах
принимается по табл. 22.
|
Марка раствора |
Наименьшая конструктивная
высота перемычек (в долях от пролета) |
|||
|
рядовых |
клинчатых |
арочных |
||
|
из кирпича |
из камня |
|||
|
25 и выше |
0,25 |
0,33 |
0,12 |
0,06 |
|
10 |
- |
- |
0,16 |
0,08 |
|
4 |
- |
- |
0,20 |
0,10 |
Примечание. Под конструктивной высотой
перемычки понимается: для рядовой перемычки - высота пояса кладки на растворе
повышенной прочности; для клинчатой и арочной перемычек - высота пояса кладки
на ребро. Конструктивная высота рядовых кирпичных перемычек должна быть не
менее 4 рядов кирпича, а перемычек из камней - не менее 3 рядов камня.
|
Марка раствора |
Величина d в долях от
расчетной высоты перемычки с |
|
|
при марке кирпича и камня
75 и выше |
при марке камня 50 и ниже |
|
|
100 |
0,1 |
- |
|
50 |
0,12 |
0,15 |
|
25 |
0,15 |
0,2 |
|
10 |
0,2 |
0,25 |
|
4 |
0,25 |
0,3 |
Примечания: 1. Под расчетной высотой
перемычки с понимается высота перемычки до уровня опирания балок или настила
перекрытия.
2. При отсутствии нагрузки на
перемычки от перекрытий или других конструкций, кроме собственного веса,
расчетная высота перемычки принимается равной 1/3 пролета.
3.Для арочных перемычек
расчетная высота принимается от уровня пят до уровня опирания балок или настила
перекрытия (включая высоту подъема перемычки).
7.193. Величина расчетного
распора Н рядовых, клинчатых и арочных перемычек определяется по формулам:
в перемычках без затяжек
![]() ; (99)
; (99)
в перемычках с затяжкой
![]() , (100)
, (100)
где М -
величина наибольшего расчетного изгибающего момента в перемычке, определяемая
как для свободно лежащей балки, от собственного веса перемычки и от давления
концов балок, прогонов и настила, опирающихся на перемычку;
с - расчетная высота
перемычки;
h0 - расстояние от верха
расчетной части перемычки до оси затяжки;
d - расстояние
кривой давления в замке от верха перемычки в замке и от низа перемычки в пятах.
Примечание. Нагрузка от собственного
веса перемычек определяется с учетом указаний п. [6.47].
7.194. Прочность кладки
перемычки в замке и на опорах проверяется на действие возникающего в перемычке
распора, который рассматривается как внецентренно приложенная в горизонтальном
направлении сила с эксцентриситетом
![]() (101)
(101)
При этом расчет растянутой
зоны перемычки по раскрытию трещин не производится.
7.195. В крайних перемычках
(у углов здания) необходимо дополнительно проверить прочность пяты на срез и
прочность углового простенка на действие распора перемычки Н.
Прочность пяты перемычки на
срез проверяется по п. [4.20]. Прочность углового простенка при отсутствии
затяжки проверяется на внецентренное сжатие в плоскости стены при действии
вертикальной продольной силы и распора Н. Величина эксцентриситета
равнодействующей на уровне подоконника не должна превышать еу=0,7у.
Если сопротивление пяты срезу
или углового простенка на внецентренное сжатие недостаточно, для восприятия
распора в перемычках требуется установка затяжек, которые заделываются в кладку
на глубину не менее 50 см от края проема. Сечение затяжек проверяется по
формуле
Н£RsAs, (102)
где Аs -
площадь сечения затяжки.
ВИСЯЧИЕ СТЕНЫ (СТЕНЫ, ОПИРАЮЩИЕСЯ НА РАНДБАЛКИ)
7.196. Висячие стены,
опирающиеся на железобетонные или стальные рандбалки, поддерживаемые колоннами
или столбчатыми фундаментами, рассчитываются на прочность при смятии в зоне над
опорами рандбалок по указаниям, приведенным в пп. [6.48-6.53].
7.197. Расчет кладки или
бетона на смятие под опорами рандбалок производится как для перемычек (по п. 7.186 и 7.187), при этом рандбалки принимаются заделанными в
опорных сечениях. Расчетные сопротивления кладки при смятии принимаются по пп.
[4.13-4.16]. Расчетные длины заделки неразрезных и однопролетных рандбалок
указаны в п. [6.51]. Расчетное сопротивление бетона при смятии определяется по СНиП
2.03.01-84.
7.198. Указания, приведенные
в пп. [6.42-6.53], распространяются на растет висячих стен на затвердевшем
растворе при отношении высоты стены к ее пролету не менее 0,5. При
неотвердевшем растворе кладка рассматривается только как нагрузка на рандбалку.
п. [6.53а].
7.199. Статический расчет
стен, опирающихся на рандбалки, может производиться также методами теории
упругости (например, методом конечных элементов с применением ЭВМ). При этом
стена и поддерживающая ее рандбалка рассматриваются как балка-стенка, состоящая
из двух идеально упругих материалов, нелинейность деформаций которых условно
учитывается уменьшением их модулей упругости, п. [6.48].
7.200. Эпюра распределения
давления в кладке висячих стен при наличии проемов принимается по указаниям п.
[6.52].
Проемы в висячих стенах
следует располагать, как правило, в одном вертикальном ряду в пределах среднего
участка между опорами. Проемы, расположенные непосредственно над рандбалками в
зонах, примыкающих к опорам, увеличивают величину напряжений в стенах и
ухудшают условия работы рандбалок.
7.201. Прочность кладки стен
при местном сжатии над опорами рандбалок следует проверять по указаниям пп.
[4.13-4.16].
7.202. В случае необходимости
висячая стена, выложенная из кирпича, керамических, бетонных или природных
камней, при высоте ряда кладки не более 150 мм может быть усилена
сетчатым армированием в зоне, расположенной над и под опорами рандбалки. В этом
случае величина расчетного сопротивления кладки при местном сжатии Rс принимается равной
расчетному сопротивлению кладки с сетчатым армированием Rsk. Высота зоны кладки, усиленной сетчатым армированием, ограничивается
сечением, в котором прочность неармированной кладки окажется достаточной.
При недостаточной прочности
висячей стены, выложенной из бетонных или природных камней с высотой ряда более
150 мм, для которых усиление сетчатым армированием является малоэффективным,
следует повысить жесткость рандбалок, что увеличит длину площади смятия.
7.203. Расчет
рандбалок должен производиться на два случая загружения: в период возведения
стен и в период эксплуатации законченного здания в соответствии с п. [6.53].
При расчете рандбалок на
нагрузки, действующие в период возведения стен, следует также учитывать
нагрузки от перекрытий, расположенных в пределах квадрата кладки высотой,
равной пролету рандбалки.
7.204. В сложных случаях
(например, при расположении проемов над опорами рандбалки, при двух или более
вертикальных рядах проемов и др.) рандбалка приближенно может быть рассчитана
на всю нагрузку от стены, принимая равномерное распределение давления в каждом
простенке, опирающемся на рандбалку. При этом принимается, что к каждому
простенку приложены нагрузки, находящиеся между осями примыкающих к простенку
проемов.
7.205. При симметричном
расположении двух вертикальных рядов проемов нагрузку, находящуюся между осями
примыкающих к простенку проемов, допускается умножать на коэффициент, равный
0,3. При этом величина опорных реакций рандбалки определяется по нагрузкам,
действующим в пределах ее длины без понижающих коэффициентов.
7.206. Поперечная сила у опор
рандбалки принимается равной равнодействующей всех нагрузок, расположенных в
пределах половины пролета рандбалки, отсекаемого наклонным сечением (черт. 52). Расчет рандбалки по наклонному
сечению на действие поперечных сил производится по пп. 3.29-3.31 СНиП
2.03.01-84.
Черт. 52. Определение
поперечной силы у опор рандбалки
1 - колонна; 2 - рандбалка
Пример 15. Расчет висячей стены
промышленного здания.
Проверить прочность наружной
кирпичной стены промышленного здания толщиной 0,38 м, опирающейся на
железобетонные однопролетные рандбалки. Стена выложена из глиняного кирпича
пластического прессования марки 100 на растворе марки 50. Рандбалки,
изготовленные из бетона марки 250, имеют трапециевидное поперечное сечение
высотой 0,45 м. Длина рандбалок, уложенных на обрезы железобетонных
фундаментов, равна 5,95 м. В стене над рандбалкой имеется дверной проем,
расположенный на расстоянии 0,4 м от грани опоры (черт. 53). Опорная реакция рандбалки за вычетом нагрузки
от собственного веса N=550 кН (55 тc). Момент инерции
приведенного сечения рандбалки Ired=264×10-5 м4.
Черт. 53.
Определение высоты пояса кладки, эквивалентного
по жесткости рандбалке
По формуле [56] п. [6.48]
определяем высоту пояса кладки Н0, эквивалентного по жесткости
рандбалке. Для бетона класса В20 Еb=2,65´104 МПа. Жесткость рандбалки равна:
0,85EbIred=0,85×2,65×104×264×10-5=59,5 МН×м2.
Расчетное сопротивление
сжатию кладки из кирпича марки 100 на растворе марки 50 находим по табл. [2] п.
[3.1]: R = 1,5 МПа. Средний предел прочности кладки определим по формуле [3]: п.
[3.20] Ru=2R=2×1,5=3 МПа. Упругая характеристика кладки a=1000, см. п. [3.21, табл.
15]. Модуль упругости кладки по формуле [7] п. [3.22] Е=0,5Е0=0,5×1000×3=1,5×103 МПа. По формуле [56] п. [6.48]
 м.
м.
Длина эпюры давления по
формуле [59] п. [6.50] без учета влияния проема
Ic=a1+s1=0,475+0,9×0,940=1,32 м.
Длина эпюры давления за
вычетом проема равна:
l1=0,475+0,4=0,875 м;
l2=lc-l1=1,32-0,875=0,445 м.
Площадь смятия Аc=0,875×0,38=0,333 м2.
В данном случае вследствие
наличия проема расчетная площадь сечения при местном сжатии равна площади
смятия, при этом Rloc=R=1,5 МПа. Максимальная величина напряжения
смятия определяется по формуле [57] п. [6.49]
![]() кПа=2,19 МПа.
кПа=2,19 МПа.
Напряжения у края проема ![]() МПа.
МПа.
Площадь эпюры давления в
пределах проема равна:
А=0,74×0,445×0,5=0,165 МН/м.
При замене площади эпюры
давления в пределах проема равновеликой площадью параллелограмма на участке стены,
расположенном над опорой рандбалки, увеличение напряжения на этом участке
составит:
![]() МПа.
МПа.
Величины краевых напряжений
на участке стены, расположенном над опорой рандбалки, составляют:
smax=2,19+0,19=2,38 МПа;
smin=0,74+0,19=0,93 МПа.
Величина коэффициента полноты
эпюры давления по формуле [17] п. [4.13] равна:
![]()
Коэффициент d=1,5-0,5y=1,15.
Расчетная несущая способность кладки над опорой рандбалки определяется по
формуле [17] п. [4.13]:
Ncc=ydRcAc=0,7×1,15×1,5×0,333=0,402 MH=402 кН<N=550 кН.
Так как несущая способность
кладки при растворе марки 50 недостаточна, принимаем раствор марки 100 на
участке стены, примыкающем к проему и расположенном над опорой рандбалки. При
этом расчетное сопротивление кладки увеличится до R=1,8 МПа, а расчетная несущая
способность кладки возрастет до 482 кН<550 кН (незначительное уменьшение
величин Н0 и lc, вызванное повышением модуля
деформации кладки, не учитывается). Поскольку повышение марки раствора не
обеспечивает требуемой несущей способности кладки, усиливаем ее на
рассматриваемом участке сетчатым армированием. Как видно из формул [3] п.
[3.20] и [7] п. [3.22], кладка с сетчатым армированием и неармированная кладка
имеют одинаковый модуль упругости, поэтому величины Н0 и lc не изменяются. Требуемое расчетное сопротивление армированной кладки
![]() кПа=2,05 МПа
кПа=2,05 МПа
По формуле [27] п. [4.30]
определяем ![]() МПа. Для армированной
кладки принимаем обыкновенную арматурную проволоку диаметром 4 мм с площадью
поперечного сечения Аs=0,126 см2=0,126
10-4 м2. Расчетное сопротивление проволоки Rs=200 МПа. Процент армирования по объему равен m=0,55×100/(2×200)=0,138. Арматурные сетки
с квадратной ячейкой укладываем через три ряда кладки по высоте. При этом
расстояние между сетками s=0,23 м. Из формулы, приведенной в п. [4.30],
определяем размер ячейки с=(2А×100)/m=(2×0,126×10-4×100) /0,138=0,08 м. При с=0,08 м по толщине стены размещается 5 стержней
сетки, которые должны быть установлены в пределах всей высоты проема.
Применение сетчатого армирования обеспечило требуемую прочность кладки под
опорой рандбалки.
МПа. Для армированной
кладки принимаем обыкновенную арматурную проволоку диаметром 4 мм с площадью
поперечного сечения Аs=0,126 см2=0,126
10-4 м2. Расчетное сопротивление проволоки Rs=200 МПа. Процент армирования по объему равен m=0,55×100/(2×200)=0,138. Арматурные сетки
с квадратной ячейкой укладываем через три ряда кладки по высоте. При этом
расстояние между сетками s=0,23 м. Из формулы, приведенной в п. [4.30],
определяем размер ячейки с=(2А×100)/m=(2×0,126×10-4×100) /0,138=0,08 м. При с=0,08 м по толщине стены размещается 5 стержней
сетки, которые должны быть установлены в пределах всей высоты проема.
Применение сетчатого армирования обеспечило требуемую прочность кладки под
опорой рандбалки.
Пример 16. Расчет висячей стены жилого
дома.
Проверить прочность наружной
висячей стены кирпичного жилого дома толщиной 0,51 м, опирающейся на железобетонные
однопролетные рандбалки. Стена выложена из силикатного кирпича марки 100 на
растворе марки 50. Рандбалка изготовлена из бетона класса В25 высотой 0,45 м.
Длина рандбалок, уложенных на обрезы железобетонных фундаментов, l=5,9 м.
Высота стены - 5 этажей, высота этажа - 2,7 м. В стене над рандбалкой имеются
два ряда симметрично расположенных оконных проемов шириной 1,5 м. Расстояние от
проема до краев рандбалки 0,85 м. Ширина межоконного простенка b1=1,2 м. Расстояние между
осями проемов b=2,7 м (черт. 54).
Черт. 54. Стена жилого дома, опирающаяся на рандбалку
Опорная реакция рандбалки с
учетом расчетных нагрузок, приходящихся на несущую висячую стену, за вычетом
нагрузки от ее собственного веса, равна N=505 кН (50,5 тc).
Усилие, приходящееся на межоконный простенок, с учетом понижающего коэффициента
0,3 равно: N1=(0,3×2 Nb)/l=(0,3×2×505×2,7)/5,9=139 кН. Момент инерции приведенного сечения рандбалки Ired=305×10-5 м4.
Для бетона класса В25 Еb=2,9×104 МПа. Жесткость рандбалки определяется по формуле 0,85EbIred=0,85×2,9×104×305×10-5= 75,2 MH×м2.
Расчетное сопротивление
сжатию кладки из силикатного кирпича марки 100 на растворе марки 50 R=1,5 МПа,
см. табл. [2] п. [3.1]. Упругая характеристика кладки a=700.
Средний предел прочности кладки Ru=2R=3,0 МПа. Модуль упругости
кладки по формуле [7] п. [3.22] равен: Е=0,5E0=0,5×700×3,0=1,05×103 МПа.
Высоту пояса кладки Н0,
эквивалентного по жесткости рандбалке, определяем по формуле [56] п. [6.48]:
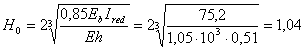 м
м
Длина участка распределения
давления от граней опоры равна s1=0,9H0=0,93 м. Длина опорного
участка рандбалки а1=0,475 м. Основание эпюры распределения давления
над опорой рандбалок равно: lс=a1+s1=1,405 м. Площадь смятия Ac=0,7165 м2.
Наибольшее напряжение над
опорой рандбалки
![]() кПа=1,23 МПа.
кПа=1,23 МПа.
Напряжение в межоконном
простенке равно ![]() кПа=0,23 МПа.
кПа=0,23 МПа.
Вследствие наличия проемов в
пролете расчетная площадь при местном сжатии равна площади смятия, т. e.Rс=R=1,5 МПа.
Расчетная несущая способность
Ncc кладки над опорой рандбалки определяется по формуле
[17] п. [4.13]:
Ncc£ydRAc=0,75×1,5×0,7165=0,806 MH=806 кН>435 кН.
Несущая способность кладки
обеспечена. Расчет на действие изгибающего момента и поперечной силы в рандбалке
в данном примере не приводится. Однако при определении величины поперечной силы
следует учитывать только часть эпюры давления, расположенную между точками
пересечения верхней грани рандбалки с невыгоднейшим наклонным сечением у опор.
В качестве примера рассмотрим конструкцию рандбалки, которая для восприятия
поперечных сил у опор армирована хомутами диаметром 10A-I с шагом 0,1 м.
Длину проекции невыгоднейшего
сечения найдем по формуле
![]() м,
м,
где k2=2 - для тяжелого бетона;
Rtb=1,0 МПа - расчетное сопротивление бетона на осевое растяжение;
b=0,5 м -
ширина рандбалки;
h0=0,4 м - рабочая высота
сечения;
Rsw=170 МПа - расчетное сопротивление поперечной арматуры растяжению для
предельных состояний первой группы;
Аw=157
10-6 м2 - площадь сечения хомутов;
u=0,1 м -
расстояние между хомутами в приопорной зоне рандбалки;
s1=(sсst/lс)=(1,23×0,93)/1,405=0,81 МПа -
напряжение над краем опоры рандбалки.
Эпюра распределения давления
на рандбалку показана на черт. 54.
Напряжение на расстоянии c0 от граней опор равно:
 ;
;
![]() МПа.
МПа.
Поперечная сила на расстоянии
c0
от опоры рандбалки равна:
Q=(s0hс0+N1)/2=(0,38×0,5×0,44+139×10-3)/2=0,112 МН=112 кН (11 тc).
Пример 17. Расчет на местное
сжатие кладки под опорным участком железобетонной перемычки.
Перемычка опирается на
кирпичный простенок длиной l=1 м, толщиной 0,38 м.
Перемычка имеет ширину поперечного сечения 0,29 м. Длина опорных участков a=0,2 м.
Расчетная нагрузка на опоре 65 кН. Кладка простенка из кирпича марки 75 на
растворе марки 25 с расчетным сопротивлением R = 1,3 МПа.
Найти расчетную несущую
способность кладки.
Продольная сжимающая сила от
местной нагрузки равна Nc=65 кН. Если под опорами
изгибаемых элементов не требуется установка распределительных плит, то
допускается принимать yd=0,75
для кладок из кирпича. Площадь смятия, на которую передается нагрузка, равна: Аc=0,29×0,20=0,058 м2.
Принимаем x=1,2.
Расчетная площадь сечения, определяемая согласно указаниям п. [4.16], равна
А=0,38+0,20×0,38=0,2204 м2.
Расчетное сопротивление
кладки на смятие Rc следует определять по формуле [18] п. [4.14]:
Rc=4R=1,2×1,3=1,56
МПа,
где 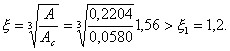
Расчетная несущая способность
кладки определяется по формуле [17] п. [4.13]:
Ncc=ydRcAc=0,75×1,56×0,058=0,06786 MH=67,86 кН>65 кН.
Поскольку нагрузка на опоре
превышает 80% несущей способности кладки, то требуется устройство сетчатого
армирования (см. п. 4.24). Определим
сечение стержней, необходимое для восприятия растягивающих напряжений при
местном сжатии. Величина наибольшей ординаты растягивающих напряжений не должна
превышать величин, определяемых по формуле
(31) stmax£0,8Rtbu=0,8×2,25×0,16=0,288 МПа. Нагрузка,
распределенная по площади опорного участка, равна:
q=65/(0,2×0,29)=1120 кПа=1,12 МПа.
Отношение v=a/l=0,20/1,0=0,2.
Наибольшая
ордината растягивающих напряжений, действующих в простенке, определяется по
формуле
![]() МПа>0,288 МПа.
МПа>0,288 МПа.
Эта величина превышает
значение, найденное по условию (29),
поэтому установка растянутой арматуры необходима.
Определим высоту растянутой
зоны по формуле
b=a(1,75v2-2,75v+1,25)=0,154м.
Равнодействующая
растягивающих усилий, подсчитанная по объему эпюры, равна Q=0,5×0,429×0,154×0,38=0,0126 МН=12,6 кН. Для восприятия этого усилия необходимо
установить арматуру в горизонтальных швах кладки. Принимаем стержни диаметром 4
мм A-I (Rs=210 МПа, Аs=0,126
см2=0,126×10-4 м2).
При толщине стены 0,38 м и шаге стержней 0,10 м в шов укладывается 4 стержня.
При двух армированных швах несущая способность стержней при растяжении
составляет RsAs=210×0,126×10-4×8=21,16×10-4 МН=21,16
кН>Q=12,6 кН. Таким образом, прочность кладки под опорным участком перемычки
обеспечена. Длина растянутой арматуры принимается не более трех длин опорных
участков «а».
АНКЕРОВКА СТЕН И СТОЛБОВ
7.207. Анкеровка стен и
столбов должна выполняться в соответствии с указаниями, приведенными в пп.
[6.35-6.39].
7.208. Стальные анкера и
связи, расположенные в наружных стенах помещений с нормальным влажностным
режимом, а также в наружных и внутренних стенах и столбах помещений с влажным
или мокрым режимом, должны быть защищены от коррозии.
При расчете анкера должны
проверяться его сечение при расчетных сопротивлениях стали, приведенных в табл.
п. [3.19], крепление к прогону, настилу или колонне, а также заделка анкера в
кладке.
Прочность заделки анкера в
кладке определяется сопротивлением кладки срезу по горизонтальным швам,
расположенным под анкером и над ним.
Распределение давления в
кладке принимается под углом 45° (черт. 55).
Расчетное усилие в анкере должно удовлетворять условию
Q<2а(а+b)(Rsq+0,8nms0), (103)
где a - глубина заделки анкера;
b - длина
поперечного штыря анкера.
Остальные обозначения
приведены в формуле [23] п. [4.20].
Черт. 55. Растет анкера
а - определение усилия в
анкере; б - кладка, вовлекаемая в работу при выдергивании анкера
ФУНДАМЕНТЫ И СТЕНЫ ПОДВАЛОВ
7.209. Проектирование
фундаментов и стен подвалов производится по указаниям, приведенным в пп.
[6.65-6.68].
7.210. Указанный в п. [6.65]
случайный эксцентриситет должен быть учтен при определении положения нормальной
силы в нижнем сечении стены первого этажа, прочность которого должна быть
проверена при внецентренном сжатии.
7.211. При толщине фундамента
меньшей, чем толщина стены первого этажа, ширина свеса стены первого этажа над
фундаментом не должна превышать 10 см.
При расчете естественного
основания случайный эксцентриситет не учитывается.
7.212. Морозостойкость
материалов, применяемых для фундаментов и стен подвалов, должна отвечать
требованиям, приведенным в п. [2.5, табл. 1].
7.213. Составы цементных
растворов для фундаментов и других конструкций, расположенных в насыщенных
водой грунтах и ниже уровня грунтовых вод, следует принимать по прил. 4.
7.214. Каменные фундаменты
могут быть ленточными и столбчатыми (отдельно стоящими).
Ленточные фундаменты обычно
устраивают под сплошными стенами с относительно неширокими проемами или с
небольшим числом проемов.
Для уменьшения объема кладки
в производственных зданиях с широкими проемами рекомендуется применять
столбчатые фундаменты с рандбалками, поддерживающими стены.
Столбчатые фундаменты следует
применять и в малоэтажных жилых и общественных зданиях в случаях, когда это
экономически оправдано.
Столбчатые фундаменты
рекомендуется располагать в углах здания на пересечениях стен и вдоль стен на
расстояниях, определяемых размерами фундаментных балок. Обычно применяют
железобетонные рандбалки, которые могут быть сборными или монолитными.
Столбчатые фундаменты могут
быть монолитными или сборными из слабоармированных железобетонных элементов.
При значительной величине эксцентриситета вертикальной нагрузки рекомендуется
проектировать фундамент несимметричным, а подошву фундамента центрировать по
равнодействующей силе.
При проектировании
фундаментов, а также стен подвалов, если предполагается их возведение зимой,
следует учитывать указания разделов
7 и 8.
7.215. Фундаменты стен
подвалов закладываются на глубине не менее 50 см ниже уровня пола подвального
помещения.
7.216. Схема нагрузок на стены
подвалов и очертания эпюр изгибающих моментов приведены на черт. 56.
Стена подвала рассчитывается
как балка с двумя неподвижными шарнирными опорами. При наличии бетонного пола
расчетная высота стен подвала принимается равной расстоянию в свету между
перекрытием подвала и поверхностью пола. При отсутствии бетонного пола
расчетная высота принимается равной расстоянию от нижней поверхности перекрытия
до подошвы фундамента.
Для удобства расчета
временную нормативную нагрузку на поверхности земли заменяют добавочным
эквивалентным слоем грунта высотой Hred, м:
![]() , (104)
, (104)
где F - нормативная нагрузка на
поверхности земли;
g
- объемная масса грунта.
Эпюра бокового давления
грунта на 1 м стены подвала представляет собой трапецию с верхней и нижней
ординатами q1 и q2:
где n1 - коэффициент перегрузки для
нагрузки на поверхности земли;
n2 - то же, для объемной массы
грунта;
H2 - высота эпюры давления
грунта;
j
- расчетный угол внутреннего трения грунта, принимается по указаниям СНиП
2.02.01-83.
Моменты в стене подвала от
бокового давления грунта могут быть определены по формуле
где H1 - расчетная высота стен
подвала;
х - расстояние от верха стены
подвала до рассматриваемого горизонтального сечения.
Если боковое давление
приложено по всей высоте стены подвала, то приближенно можно считать, что
максимальное значение Mx будет на расстоянии х=0,6H1:
Если ось вышележащей стены
совпадает с осью стены подвала, то нагрузка от вышележащих этажей считается
приложенной центрально.
Расчетом на внецентренное
сжатие проверяют сечения стены, в которых моменты имеют максимальные значения.
Черт. 56. Схема нагрузок на стену подвала и эпюры моментов
ПОДПОРНЫЕ СТЕНЫ
7.217. Подпорные стены из
каменной кладки целесообразно применять только при относительно небольшой их
высоте. При высоте более 4 м подпорные стены рекомендуется выполнять из
железобетона.
Пример 18. Расчет стены подвала.
Проверить несущую способность стены подвала кирпичного здания. Стена подвала
высотой Н=2,8 м выполнена из крупных пустотелых бетонных блоков толщиной 40 и
высотой 58 см, изготовленных из тяжелого бетона марки 100. Пустотность блоков
по площади среднего горизонтального сечения 25, а по объему - 15%. Кладка стен
подвала выполнена на растворе марки 50. Расчетная высота стены подвала от
уровня бетонного пола до нижней поверхности перекрытия Н=2,65 м (черт. 57). Расчетная нагрузка на 1 м стены
подвала от кирпичной стены первого этажа толщиной 51 см N=150 кН
(15 тc).
Черт. 57. Расчет стены
подвала
а - схема приложения вертикальных нагрузок; б - эпюра бокового давления грунта; в - суммарная эпюра изгибающих моментов
Стена первого этажа
расположена с эксцентриситетом относительно оси подвала е1=5,5 см.
Расчетная постоянная
нагрузка на 1 м стены подвала от опирающегося на нее перекрытия над подвалом N2=22
кН (2,2 тс) приложена с эксцентриситетом по отношению к стене подвала е2=16
см.
Объемная масса грунта в
насыпном состоянии g=1600 кг/м3=16
кН/м3. Расчетный угол внутреннего трения грунта j=38°; нормативное значение поверхностной
нагрузки от грунта в насыпном состоянии Р=10 кН/м2.
Приведенная толщина грунта
от временной нагрузки
![]() м.
м.
Коэффициенты перегрузки для
временной нагрузки и объемной массы грунта
n1=n2=n=1,2.
Верхняя и нижняя ординаты
эпюры бокового давления грунта на 1 м стены подвала определяются по формулам (105) и (106):
q1=1,2×16×0,625×0,238=2,86 кН/м ;
q2=1,2×16(0,625+2,65)0,238=14,97
кН/м.
Изгибающие моменты от
давления грунта определяем в двух сечениях стены подвала: в сечении 1-1,
расположенном на расстоянии 0,4H=0,4×2,65=1,06 м от верха стены и
в сечении 2-2 - на расстоянии 0,6H=0,6×2,65=1,59 м от верха стены,
в котором величина изгибающего момента от давления грунта имеет наибольшее
значение.
По формуле (107) при расположении сечения на расстоянии
0,4H от верха стены, принимая Н2=Н:

![]() кН×м.
кН×м.
Изгибающий момент от
вертикальных нагрузок в сечении, расположенном у верха стены подвала,
определяется с учетом случайного эксцентриситета е=4 см [п. 6.65], так как
толщина стены подвала меньше, чем стены первого этажа.
Максимальная величина
момента
М=150(0,055+0,04)-22×0,16=10,73 кН×м.
Суммарные изгибающие моменты
в стене подвала:
в сечении, расположенном на
расстоянии 0,4H от верха стены,
М04=10,73×0,6+7,17=13,61 кН м;
в сечении, расположенном на
расстоянии 0,6H от верха стены,
М06=10,73×0,4+7,85=12,14 Н×м.
Проверку прочности стены
подвала производим в сечении 1-1, расположенном на расстоянии 0,4H от
верха стены,
N=150+22+1,06×0,4×24,0×0,85×1,1=181,5 кН.
Прочность стены подвала
проверяем при внецентренном сжатии с эксцентриситетом
![]() м.
м.
Расчетная несущая
способность стены Ncc определяется по формуле п. [4.7]:
![]()
По п. [4.7], формула [15]
![]()
В данном случае при h=40 см mg=1, см. n. [4.7].
Упругая характеристика кладки
из крупных пустотелых бетонных блоков при отношении
![]()
a=1500.
Коэффициент продольного
изгиба по табл. [18] п. [4.2] j=0,97.
Высота сжатой зоны
hс=h-2e0=0,40-2×0,075=0,25
м;
![]()
![]()
Расчетное сопротивление
кладки из крупных пустотелых бетонных блоков, изготовленных из бетона марки
100, при растворе марки 50 и пустотности блоков по среднему горизонтальному
сечению 25% определяется по п. [3.12]:
R=2,7×0,5=1,35 мН/м2.
Расчетная несущая способность
стены равна:
![]()
Площадь сечения (брутто)
А=0,4×1,0=0,4м2.
Коэффициент w
определяется по п. [4.7], табл.[19]:
![]()
![]() кН.
кН.
Прочность стены подвала
достаточна.
7.218. Подпорные стены должны
быть запроектированы таким образом, чтобы была исключена возможность их
опрокидывания и скольжения, обеспечены несущая способность стены и грунта в ее
основании и в необходимых случаях трещиностойкость.
7.219. Подпорные стены могут
быть безреберными и ребристыми. Как правило, проектируют их уширенными книзу,
рассчитывая как консольные балки прямоугольного или таврового сечения.
Каменные вертикальные
подпорные стены (черт. 58) высотой не
более 4 м и при горизонтальной поверхности земли допускается рассчитывать по
указаниям настоящего раздела.
При передаче давления грунта
на вертикальную поверхность подпорной стены (черт.
59), если земля ограничена горизонтальной плоскостью, распределение
горизонтального давления грунта по высоте стены определяется формулами (105) и (106).
Величину нормативной нагрузки
на поверхность земли следует принимать согласно п. 7.216.
Сечения подпорной стены
проверяют на внецентренное сжатие и срез по горизонтальным неперевязанным швам
кладки.
В расчетную площадь среза
включается только площадь сжатой зоны сечения, определяемая при расчете на
внецентренное сжатие.
При проверке подпорных стен
на опрокидывание и скольжение собственный вес их принимается с коэффициентом
перегрузки 0,9.
Подпорные стены одноэтажных
складов сыпучих материалов и заглубленных одноэтажных зданий, воспринимающие
значительные горизонтальные давления при небольших вертикальных нагрузках,
рекомендуется рассчитывать как балки с верхней шарнирной и нижней защемленной
опорами. Защемление нижней опоры стен обеспечивается фундаментами, выполненными
в виде прямоугольных участков кладки, перпендикулярных продольной оси стены.
Расположение фундаментов и пилястр совпадает (см. черт. 59).
Размеры фундаментов
определяются из условия совмещения их оси с положением равнодействующей нормальной силы в
основании стены при максимальных горизонтальных и минимальных вертикальных
нагрузках.
Черт 58. Продольные стены
разных профилей
а - прямоугольного; б - трапецеидального с
наклонной передней гранью; в - трапецеидального с наклонной задней гранью; г -
наклонного в сторону засыпки; д - с выступающим передним нижним ребром; е -
ступенчатого; ж - таврового
Черт. 59. Фундаменты под
наружными стенами одноэтажных складских зданий для сыпучих материалов
1 - контрфорс; 2 -
стена; 3 - пилястра; 4 - давление сыпучего материала; 5 - железобетонная или
рядовая перемычка между фундаментами; б - фундамент
ДЕФОРМАЦИОННЫЕ ШВЫ
7.220. Деформационные швы в
стенах и перекрытиях каменных зданий устраиваются в целях устранения или
уменьшения отрицательного влияния температурных и усадочных деформаций, осадок
фундаментов, сейсмических воздействий и т. п.
7.221.
Температурно-усадочные швы устраиваются в местах возможной концентрации
температурных и усадочных деформаций, которые могут вызвать в конструкциях
недопустимые по условиям эксплуатации и долговечности разрывы, трещины, а также
перекосы и сдвиги кладки.
7.222. Расстояния между
температурно-усадочными швами следует определять расчетом в соответствии с
указаниями прил. 11.
Максимальные расстояния между
температурно-усадочными швами в неармированных наружных стенах принимаются в
соответствии с указаниями п. [6.79], без расчета на действие температуры и
усадки.
Указанные в п. [6.79]
расстояния могут быть увеличены путем армирования кладки стен по расчету.
Примечание. Разрезка зданий
температурными швами в соответствии с требованиями п. [6.79] уменьшает, но не
устраняет полностью температурные усилия в стенах и перекрытиях. Поэтому во
всех случаях необходимо производить расчетную проверку на действие температуры
и усадки отдельных узлов и сопряжении конструкций, в которых возможна
концентрация температурных деформаций и напряжений. Проверка выполняется в
соответствии с указаниями прил. 11.
7.223. Температурные швы в
стенах зданий, имеющих протяженные (20 м и более) стальные или армированные
бетонные включения или арматуру (балки, перемычки, плиты перекрытий, арматурные
пояса и т. п.), устраивают по концам армированных участков и включений, где
обычно происходят концентрация температурных деформаций и образование трещин и
сквозных разрывов. Примеры устройства температурных швов в указанных случаях
показаны на черт. 60.
7.224. Температурные швы в
стенах могут не устраиваться при условии армирования кладки в местах обрыва
арматуры или по концам включения по расчету в соответствии с указаниями прил. 11.
В зданиях с продольными
несущими стенами и сборными перекрытиями, имеющих частую (через 1-2 м) разрезку
поперечными швами (см. черт. 60, б),
температурные швы при ширине проемов не более 2,5 м и отсутствии протяженных
армированных включений могут не устраиваться, независимо от длины и этажности
здания и климатических условий района застройки.
При этом раскрытие трещин в
стенах и по концам армированных перемычек не должно превышать допустимых
значений по табл. 1 прил. 11.
7.225. Конструкция
температурных швов в стенах, перекрытиях и покрытиях каменных зданий должна
удовлетворять следующим требованиям:
а) температурные швы в
наружных и внутренних стенах, перекрытиях и покрытиях (крышах) зданий
рекомендуется устраивать в одной плоскости на всю высоту здания, исключая
фундаменты, разрезка которых является не обязательной; вопрос о разрезке швами
только наружных или только внутренних стен решается отдельно при достаточном
обосновании;
б) температурные швы в
стенах должны совпадать со швами в железобетонных или стальных конструкциях
(перекрытиях, каркасах, обвязочных балках и т. п.), имеющих со стенами
конструктивную связь (заделка, анкеры и т. п.), а также должны совпадать с
другими видами швов (осадочными, сейсмическими, монтажными и т. п.);
в) температурные швы должны
обладать достаточной горизонтальной подвижностью (до 10-20 мм) как при сжатии,
так и при расширении шва, а конструкция шва должна обеспечивать удобную
установку, контроль и ремонт герметизирующих устройств и утеплителя;
Черт. 60. Примеры устройства
температурных швов в стенах каменных зданий с армированными включениями
(перекрытия, балки, армированные пояса)
а - при расположении армированных включений в средней части здания; б - то же, в крайней части; в - при железобетонном покрытии (крыше) со швом; г - при фундаментных балках со швом; д - примеры заделки армированных включений в кладку стен; 1 - перекрытие; 2 - железобетонная балка; 3 - металлическая балка; 4 - арматура; 5 - температурный шов в армированных элементах (плитах, балках); 6 - то же, в каменных стенах (пунктир) ; 7 - сборные перекрытия с поперечными швами
г) ширина температурного шва
определяется расчетом, но должна быть не менее 20 мм;
д) температурные швы
наружных стен должны быть водо- и воздухонепроницаемыми и непромерзаемыми, для
чего они должны иметь утеплитель и надежную герметизацию в виде упругих и
долговечных уплотнителей из легкосжимаемых и несминаемых материалов (для зданий
с сухим и нормальным режимами эксплуатации), металлических или пластмассовых
компенсаторов из коррозиеустойчивых материалов (для зданий с влажным и мокрым
режимами).
7.226. Герметизация температурных
швов в наружных стенах осуществляется с помощью металлических и пластмассовых
компенсаторов (черт. 61, д, б)
или с помощью упругих уплотнителей (черт.
61, в, г).
Герметизация швов внутренних
стен производится с помощью уплотнителей. Использование для этих целей
компенсаторов должно быть обосновано.
Черт. 61. Устройство
температурных швов в наружных стенах зданий
а, б - с сухим и нормальным режимами эксплуатации; в, г - с влажным и мокрым режимами; 1 - утеплитель (толь и рубероид с утеплителем или пороизол, гернит); 2 - штукатурка; 3 - расшивка; 4 - компенсатор; 5 - антисептированные деревянные рейки 60´60 мм; 6 - утеплитель; 7 - вертикальные швы, заполненные цементным раствором
В зависимости от влажностного режима внутренних помещений компенсаторы могут изготовляться из коррозиеустойчивого листового металла (оцинкованная или нержавеющая сталь, медь, свинец и т. п.) или специальных пластмасс (поливинилхлорид, неопрен, бутил и т. п.). Концы компенсаторов должны плотно заделываться в бетон или кладку стен, как показано на черт. 61.
Использование для
герметизации швов в наружных стенах уплотнителей из упругих поризованных
материалов (пороизол, гернит и т. п.), а также пакетов из рубероида или толя с
прокладкой упругого утеплителя между слоями этих материалов (см. черт. 61, а, б) допускается только
для зданий с сухим и нормальным влажностными режимами при ширине температурных
швов не более 30 мм. В этом случае температурный шов в стене выполняется. с
уступами кладки (шпунт, четверть, см. черт.
61, а, б).
При использовании компенсаторов кладка швов выполняется без уступов. Герметизация швов с помощью уплотнителей производится с двух сторон (снаружи и изнутри).
Примеры устройства
температурных швов в железобетонных утепленных и неутепленных крышах зданий
показаны на черт. 62.
7.227. При опирании
перекрытий на несущие поперечные стены, ригели рам каркасов и т. п.
температурные швы устраиваются в виде двух спаренных стен (черт. 63, д, б), ригелей и колонн каркасов или в
виде швов скольжения плит перекрытий, опирающихся на консольные выпуски,
заделанные в поперечные стены или в специальные штрабы (черт. 63, в, г). Для обеспечения скольжения под
опоры плит следует укладывать два слоя кровельного железа, как показано на черт. 63.
Черт. 62. Примеры устройства
температурных швов в железобетонных крышах
а - с гребнем из бетона; б - с гребнем из кирпичной кладки; в - без гребня; 1 - деревянные антисептированные пробки; 2 - компенсатор из кровельного железа; 3 - доска 50´120 мм; 4 - бетон класса В12,5; 5 - рулонная кровля; 6 - кирпичная кладка на растворе марки 100; 7 - скоба (-3´40) через 500 мм; 8 - железобетонные плиты
Черт. 63. Температурные швы в
зданиях с поперечными несущими стенами
а, б - в виде двух спаренных
стен; в - в виде скользящего опирания плит перекрытий в штрабе поперечной
стены; г -то же, на консольную плиту, заделанную в стену; 1 - утеплитель (толь
или рубероид с утеплителем или пороизол, гернит); 2 - два слоя оцинкованного
железа; 3 - податливая связь - ограничитель диаметром 6-8 мм через 1,5-2 м; 4 -
нащельник; 5 - железобетонная консоль
7.228. Температурные швы в
зданиях с продольными несущими стенами устраиваются у внутренних поперечных
стен или перегородок (черт. 64).

Черт. 64. Температурные швы в
зданиях с продольными несущими стенами
а - в местах сопряжения
продольной стены с поперечной; б - то же, у поперечной перегородки; 1 -
утеплитель (толь или рубероид с утеплителем или пороизол, гернит); 2 - расшивка
шва; 3 - нащельник; 4 - просмоленная пакля; 5 - перегородка
7.229. Штукатурка в местах
устройства температурных швов должна расшиваться (черт. 64, а, б).
В жилых,
общественных и бытовых помещениях температурные швы рекомендуется закрывать со
стороны помещений нащельниками (см. черт.
64).
ОСАДОЧНЫЕ ШВЫ
7.230. Осадочные швы в стенах
и перекрытиях зданий при обычных грунтовых условиях устраиваются в следующих
случаях:
при возможности больших
неравномерных осадок по расчету, превышающих допустимые по нормам;
при сопряжении участков
здания, расположенных на разнородных, или обжатых и необжатых грунтах, при
разновременном возведении этих частей;
при пристройке к существующим
зданиям;
при разнице высот отдельных
частей зданий, превышающей 10 м, если в проекте не предусмотрены
распределительные пояса для более равномерного распределения давления в кладке;
при значительной разнице в
ширине подошвы и глубине заложения фундаментов соседних стен;
при
устройстве разнотипных фундаментов в плане здания (под одной частью здания
фундаменты ленточные, под другой - свайные или сплошная плита).
Осадочные швы зданий,
возводимых в районах с особыми грунтовыми условиями (просадочными,
вечномерзлыми грунтами, на подрабатываемых территориях и т. п.), а также
сейсмические швы устраиваются в соответствии с требованиями специальных норм.
7.232. Осадочные швы должны
разрезать здание на всю высоту, включая фундаменты, и выполняться в виде двух
спаренных стен или рам.
Конструкция осадочных швов
должна обеспечить беспрепятственную осадку (до 10-20 мм) и повороты примыкающих
стен относительно друг друга.
Ширина швов определяется
расчетом, но должна быть не менее 20 мм в свету.
ТОНКОСТЕННЫЕ СВОДЫ ДВОЯКОЙ КРИВИЗНЫ
7.232. При проектировании
тонкостенных сводов двоякой кривизны1 следует соблюдать требования,
приведенные в пп. [6.69-6.74].
1 Предложение канд. техн. наук
А. И. Рабиновича (а.с. № 65661 от 30.10.47).
7.233.
Тонкостенные своды двоякой кривизны из кирпича или камней прямоугольной формы
применяются в качестве покрытий производственных, общественных, складских и
сельскохозяйственных зданий при пролетах до 24 м. Кирпичные своды выполняются
толщиной в 1/4 кирпича (кирпич в сводах укладывается плашмя). Своды двоякой
кривизны имеют волнообразную поверхность, обладающую большой жесткостью, что
позволяет резко уменьшить их толщину и увеличить размеры перекрываемых пролетов
по сравнению с массивными каменными сводчатыми покрытиями (черт. 65). Перевязка кладки кирпичных сводов показана на черт. 66, а сводов из бетонных камней - на
черт. 67 (размеры - в см).
Черт. 65. Общим вид свода
1 - затирка раствором; 2 -
свод толщиной в 1/4 кирпича
Черт. 66. Перевязка кладки сводов толщиной в 1/4 кирпича
Черт. 67. Перевязка кладки сводов из камней толщиной 9 см
Для лучшего заполнения швов
верхнюю поверхность кирпичных сводов в процессе кладки затирают раствором.
7.234. Ширина волн сводов
принимается, как правило, равной 2 м, а высота волн составляет от 1/2,5 до 1/5
ширины волны, в зависимости от величин пролета сводов и воспринимаемых ими
нагрузок.
Своды выкладывают из целого
кирпича или камней, приколка их по месту производится только при замыкании волн
свода в ключе.
При пролетах сводов более 21
м несущую способность их следует повышать путем заполнения пазух между волнами
тяжелым бетоном классов В7,5 - В12,5 на половину их высоты (черт. 68).
Черт. 68. Своды комплексной
конструкции
1 - тяжелый бетон
7.235. Своды двоякой кривизны
выкладывают по передвижной инвентарной металлодеревянной или деревянной
опалубке, служащей для кладки двух волн свода. Законченные кладкой волны
выдерживают на опалубке в течение 12 ч при температуре 10°С
и выше. При более низкой положительной температуре продолжительность
выдерживания сводов на опалубке увеличивают до 18-24 ч.
7.236. Распор сводов, опирающихся на
стены или колонны, воспринимается затяжками из круглой стали (гладкой класса A-I или
периодического профиля классов А-II и А-III), располагаемыми под гранями
взаимного примыкания смежных волн свода; распор может также восприниматься
контрфорсами или поперечными стенами помещений, примыкающих с обеих сторон к
перекрываемому сводами пролету. В складских зданиях и в некоторых типах
производственных помещений целесообразно опоры сводчатых покрытий, имеющих
большую стрелу подъема, располагать на уровне земли, при этом распор
воспринимается фундаментами или затяжками, расположенными в плоскости пола.
Концы затяжек закрепляются в опорных узлах шайбами, гайками и контргайками. Для
облегчения транспортирования и упрощения установки затяжек они изготовляются из
нескольких звеньев, шарнирно скрепленных между собой при помощи приваренных к
ним петель (черт. 69). При пролете
сводов свыше 18 м затяжки поддерживаются двумя подвесками, расположенными в
третях пролета.
Примечание. Петли и ослабленные резьбой
утолщенные концы затяжек изготовляются из стали класса A-I.
7.237. В сводах допускается
устройство проемов в пределах всей ширины волны для поперечных фонарей верхнего
света. Такие проемы следует располагать не чаще чем через две смежные волны
свода. Края волн свода, примыкающих к фонарным проемам, должны быть усилены
железобетонными ребрами треугольного очертания, размещаемыми в пазухах между
волнами в пределах всего перекрываемого сводом пролета. Проемы небольших
размеров для зенитных фонарей, вентиляционных шахт, вытяжных труб и т. п.
окаймляют рамками из стальных уголков, которые устанавливают в процессе кладки
свода.
7.238. Своды, перекрывающие
отапливаемые помещения, утепляют плитными теплоизоляционными материалами
(минераловатные и полимерные плиты, фибролит и т. п.) или засыпками
(керамзитовый гравий, шлак и т. п.). Плитные утеплители должны иметь небольшие
размеры, обеспечивающие возможность укладки их по криволинейной поверхности
свода. До укладки утеплителя верхняя поверхность свода покрывается пароизоляционным
слоем (обычно битумная обмазка). Стяжка из цементного раствора или асфальта,
наносимая на верхнюю поверхность утеплителя, служит основанием для кровли из
рулонных материалов. Наряду с рулонными кровлями для гидроизоляции сводов с
большой стрелой подъема допускается применение мастичных кровель.


Черт. 69. Затяжка свода
а - затяжка; б - деталь стыка затяжки; в - подвеска; 1 -утолщенный конец затяжки; 2 - петли; 3 - звено затяжки; 4 - сварка; 5 - квадратная шайба d³10 мм; 6 - отверстие для подвески - оставляется при кладке свода; 7 - подвеска диаметром 10-12 мм; 8 - шайба d=5-6 мм
7.239. Для кладки сводов,
перекрывающих помещения с повышенной влажностью воздуха, не допускаются к
применению: силикатный кирпич, глиняный кирпич полусухого прессования, шлаковый
и трепельный кирпич и камни из ячеистого бетона.
7.240. Для кладки сводов и
их пят следует применять растворы на обычном портландцементе. Шлаковый и
пуццолановый портландцемента, а также другие виды цементов, медленно твердеющих
при пониженных положительных температурах, применять не допускается.
7.241. Своды двоякой
кривизны рассчитываются по условной расчетной схеме как плоские двухшарнирные
арки. В расчет вводится поперечное сечение одной волны свода. Своды
рассчитываются на постоянную нагрузку (собственный вес свода, утеплителя,
гидроизоляционного ковра и т. п.) и одностороннюю временную нагрузку от снега,
определяемую по СНиП
2.01.07-85 и распределенную на половине пролета свода (черт. 70). Сводчатые покрытия многопролетных зданий
рассчитываются на снеговую нагрузку, распределенную по покрытию неравномерно, с
учетом образования снеговых мешков согласно СНиП 2.01.07-85.
Черт. 70. Расчетная схема свода
7.242. В сводчатом покрытии
подлежат расчету свод, затяжка и опорный узел, а также контрфорсы или
поперечные стены, если они воспринимают распор сводов.
При расчете затяжек, опорных
узлов, стен, колонн, контрфорсов и других элементов, воспринимающих распор и
вертикальные реакции сводов, снеговая нагрузка принимается равномерно
распределенной по всему пролету свода. При многопролетных зданиях принимаются
схемы распределения снеговой нагрузки, приведенные в СНиП 2.01.07-85,
при которых величины распора и вертикальных реакций сводов имеют наибольшие
значения. Расчетные нагрузки от собственного веса свода, а также нагрузки от
теплоизоляционных плит, засылок и стяжек принимаются с коэффициентами
перегрузки, приведенными в СНиП 2.01.07-85.
Ветровую нагрузку следует
учитывать лишь для сводов с большой стрелой подъема при f/l>1/3,
а также при больших величинах скоростных напоров ветра (для V-VII
ветровых районов). Расчет сводов на температурные воздействия не производится.
Сосредоточенные нагрузки от
вентиляционных шахт, подвесного грузоподъемного оборудования и т. п. условно
распределяют на две волны свода.
7.243. При расчете сводов со
стрелой подъема в ключе f³l/5
следует учитывать вызываемое уклоном покрытия увеличение постоянной нагрузки g,
распределенной по горизонтальной проекции свода в направлении от ключа к пятам
(см. черт. 70) по кривой
где gx - величина дополнительной
постоянной нагрузки, вызываемой уклоном покрытия в сечениях, отстоящих на
расстоянии х от опоры, Н/м (кгс/м);
g - постоянная нагрузка в
ключе свода, Н/м (кгс/м);
j
- угол наклона к горизонту касательной к оси свода в рассматриваемом сечении.
7.244. Очертание оси сводов и
граней примыкания смежных волн для сводов со стрелой подъема f/l³1/5 рекомендуется принимать
по цепной линии, а при f/l< 1/5 - по дуге
окружности. Очертание поперечного сечения волн сводов принимается по квадратной
параболе.1
Для сводов, очерченных по
дуге окружности и по цепной линии, величины опорных реакций при нагрузках,
приведенных в табл. 2 прил. 9*,
принимают как для сводов параболического очертания. При других случаях
загружения сводов распределенными и сосредоточенными нагрузками опорные реакции
следует определять по таблицам, приведенным в «Справочнике проектировщика».
1 Величины ординат цепной
линии, окружности и параболы через 1/20 пролета, а также тангенсы углов наклона
касательных к этим кривым приведены в табл. 1 прил. 9.
* В табл. 2 прил. 9 косинусоидальная нагрузка, определяемая формулой (109), заменена близкой
к ней параболической.
7.245. Изгибающие моменты и
нормальные силы в поперечных сечениях свода определяют по формулам:
М=М0-Ну; (110)
N=Q0sinj+Hcosj, (111)
где М0 и Q0 - изгибающий момент и
поперечная сила в соответствующем сечении простой балки пролетом l;
у и j - ордината и угол наклона к
горизонту касательной к оси свода в рассматриваемом сечении (см. черт. 70), принимаемые по табл. 1 прил. 9.
Изгибающие моменты и
поперечные силы в простой балке при параболической нагрузке в сечении,
расположенном на расстоянии х от левой опоры (табл. 2 прил. 9), определяют по формулам:
![]() (112)
(112)
![]() (113)
(113)
Величина g1 определяется по формуле (109) при значении в
опорном сечении VA=0,l67g1l;
величина g1-gx вычисляется по формуле
![]() (114)
(114)
7.246. Расчет сводов
производится на внецентренное сжатие п. [4.7, формула (13)]. Прочность сводов
проверяется в сечениях с максимальными положительными и отрицательными
изгибающими моментами, которые при односторонней снеговой нагрузке (см. черт. 70) возникают в четвертях пролета.
Наибольшая величина
эксцентриситета в сводах ![]() не должна превышать для основных сочетаний
нагрузок 0,7у, где у - расстояние от оси, проходящей через центр тяжести
сечения до края сечения в сторону эксцентриситета.
не должна превышать для основных сочетаний
нагрузок 0,7у, где у - расстояние от оси, проходящей через центр тяжести
сечения до края сечения в сторону эксцентриситета.
Расчетные характеристики
различных поперечных сечений сводов из кирпича и камней приведены в табл. 3 прил. 9.
При определении коэффициента
продольного изгиба j расчетная длина свода l0 принимается равной 0,55, где
S - длина оси свода, определяемая по табл. 4 прил. 9.
Величину площади сжатой зоны
Аc определяют из условия совпадения центра тяжести
площади Аc с точкой приложения нормальной силы N (черт. 71), пользуясь методом
последовательного приближения.
Черт. 71. Сжатая зона
поперечного сечения свода
а - при приложении нормальной силы выше оси, проходящей через центр тяжести сечения; б - при приложении нормальной силы ниже оси, проходящей через центр тяжести сечения
При приложении нормальной силы N выше оси x0-x0, проходящей через центр
тяжести поперечного сечения волны свода (при положительном изгибающем моменте,
см. черт. 71), площадь Аc
определяется как разность площадей, ограниченных параболами 1, 2, 3 и 4, 5,
6**. При определении площади Аc задаются расстоянием от
нижней грани сечения до границы сжатой зоны у1. Для первого
приближения можно принять у1=2,8e0. При расчете сечения
принимают то значение площади Аc, при котором расстояние от
нижней грани сечения до ее центра тяжести z»у0+e0.
** Площадь
параболы равна 2/3 произведения основания параболы на ее высоту. Расстояние
центра тяжести площади, ограниченной параболой, от ее основания равно 0,4
высоты параболы.
Величина z определяется как отношение разности статических моментов площадей, ограниченных параболами 1, 2, 3 и 4, 5, 6, относительно нижней грани сечения волны свода к площади сжатой зоны Ас.
При приложении силы N ниже
оси x0-x0 (отрицательный изгибающий
момент, см. черт. 71) площадь Ас
и статический момент ее относительно нижней грани сечения определяют как сумму
и разность следующих площадей и их статических моментов: 1, 2, 4, 5
(прямоугольник) + 2, 3, 4 - 6, 3, 7 + 8, 9, 10 - 1, 9, 5. Для первого
приближения можно принять у1=h-e0. Принимается то значение Ас,
при котором
z»у0-e0.
Размеры оснований парабол
определяются по формулам:
![]() (115)
(115)
![]() (116)
(116)
Обозначения приведены на черт. 71. Угол a
определяется по величине
![]() (117)
(117)
Примечания: 1. Влияние длительного
действия нагрузки на несущую способность сводов не учитывается, и коэффициент mg принимается равным единице, так как во всех случаях радиусы инерции
поперечных сечений сводов r>8,7 см.
2. При расчете сводов
коэффициент gс см. п. [3-11], принимают
равным единице независимо от площади сечения волны.
3. При расчете сечений сводов, в которых
пазухи между волнами заполняются тяжелым бетоном (см. черт. 68), расчетное сопротивление бетона, в запас
прочности, принимается равным расчетному сопротивлению кладки свода, и в
поперечное сечение волны свода включается бетонное заполнение.
7.247. При
восприятии распора сводов затяжками (см. черт.
69) расчетное сопротивление стали принимают как для арматуры по СНиП
2.03.01-84. Концы затяжек закрепляют в опорных узлах шайбами, гайками и
контргайками. Для облегчения транспортирования и упрощения установки затяжек
они изготовляются из нескольких звеньев, шарнирно скрепленных между собой при
помощи приваренных к ним петель. Площадь сечения одной ветви петель в стыках
затяжек определяют по усилию, принимаемому с коэффициентом 0,7 от усилия в
основных элементах затяжек. Размеры шайб определяют из условия прочности кладки
при смятии. Независимо от результатов расчета размеры шайб принимаются не менее
150´150 мм.
7.248. Пяты свода имеют
наклонные поверхности, нормальные к оси свода в опорных узлах (черт. 72). Ступенчатая поверхность пят
затирается раствором в местах примыкания свода. Опорные узлы сводов, распор
которых воспринимается затяжками, должны иметь выносные пяты, повышающие
устойчивость опорных узлов при действии распора сводов.
При восприятии распора
затяжками в опорных узлах под гранями волн свода устанавливаются стальные
опорные элементы из уголков и полосовой стали, позволяющие увеличить вынос пят
до требуемых размеров.
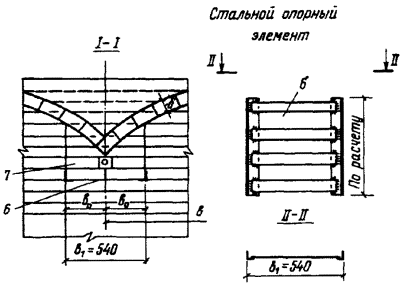
Черт. 72. Опорный узел свода
двоякой кривизны
1 - ось, проходящая через центр тяжести поперечного сечения свода; 2 - цементная или асфальтовая стяжка; 3 - рулонный ковер; 4 - шайба, гайка, контргайка; 5 - ось стены; 6 - стальной элемент из уголков; 7 - очертание пяты между стальными элементами; 8 - вынос пяты в пределах затяжек; 9 - затяжка; 10 - забутка пазух; 11 - кладка свода; 12 - пароизоляция; 13 - утеплитель
7.249. При расчете опорных
узлов сводов с затяжками (см. черт. 72)
следует учитывать изгибающий момент, возникающий вследствие смещения затяжки
относительно пересечения осей свода и стены. В расчетном сечении стены III-III,
расположенном под затяжками, величина эксцентриситета приложения нормальной
силы ![]() (N -
вертикальная опорная реакция свода и вес верхней части стены, расположенной
выше расчетного сечения) должна быть не более 0,7у, где у - расстояние от оси
стены до ее наружной грани. Для соблюдения этого условия вынос опорных стальных
элементов относительно оси стены а следует определять по формуле
(N -
вертикальная опорная реакция свода и вес верхней части стены, расположенной
выше расчетного сечения) должна быть не более 0,7у, где у - расстояние от оси
стены до ее наружной грани. Для соблюдения этого условия вынос опорных стальных
элементов относительно оси стены а следует определять по формуле
![]() (118)
(118)
Вынос пяты свода на участках
между опорными элементами относительно оси стены a1 определяется по формуле
![]() (119)
(119)
Обозначения приведены на черт. 72.
Прочность стены в расчетном
сечении III-III при внецентренном сжатии
должна быть проверена по формуле [13].
7.250. При отсутствии затяжек
(п. 7.236) опоры, воспринимающие распор
сводов, должны быть рассчитаны на внецентренное сжатие, срез и главные
растягивающие напряжения по неперевязанным швам кладки при действии распора
сводов. В расчетную площадь среза включается только площадь сжатой зоны сечения
Ас, определяемая при расчете на внецентренное сжатие. Предельная
величина усилия, воспринимаемого горизонтальными неперевязанными швами кладки,
уменьшается путем умножения на коэффициент 0,8.
7.251. При расстояниях между
поперечными стенами, не превышающих приведенные в п. [6.7], сводчатые покрытия
рассматриваются как жесткие опоры для продольных стен или колонн. При больших
расстояниях между поперечными стенами продольные стены зданий со сводчатыми
покрытиями рассчитываются как стойки рам, заделанные в грунт и шарнирно
связанные со сводчатым покрытием. В этом случае сводчатое покрытие является
упругой опорой для стен.
8. ПРОЕКТИРОВАНИЕ
КАМЕННЫХ КОНСТРУКЦИЙ ЗДАНИЙ,
ВОЗВОДИМЫХ В ЗИМНЕЕ ВРЕМЯ
8.1. Проектирование каменных
конструкций зданий, возводимых в зимнее время, следует выполнять с учетом
указаний разд. 7 СНиП II-22-81 и настоящего раздела.
При разработке проектов
каменных зданий необходимо предусматривать возможность их возведения одним из
способов, приведенных в п. [7.1].
8.2. Принятый в проекте
способ возведения здания должен обеспечивать прочность и устойчивость
конструкций как в период их строительства, так и при последующей эксплуатации.
Он должен обосновываться технико-экономическими расчетами и обеспечивать
оптимальные показатели стоимости, трудоемкости, расхода цемента,
электроэнергии, топлива и т. п.
8.3. Для повышения уровня
индустриализации и надежности, а также снижения трудозатрат в проектах каменных
зданий рекомендуется предусматривать возможность замены ручной кладки
простенков, внутренних стен и других конструкций на блоки заводского или
полигонного изготовления из кирпича, керамзитобетона и т. п.
8.4. Каменные здания высотой
до 4 этажей разрешается, при соответствующем расчетном обосновании, возводить
способом замораживания на обыкновенных (без противоморозных добавок) растворах
не ниже марки 10 при условии обеспечения достаточной несущей способности
конструкций в период оттаивания (при нулевой прочности раствора).
Этот способ
позволяет возводить малоэтажные здания без применения дефицитных химических
добавок и получать значительную экономию цемента за счет того, что кладку на
растворах с противоморозными добавками необходимо выполнять на растворе не ниже
марки 50.
8.5. В проектах каменных
зданий, возводимых в зимних условиях, следует указывать:
марку кирпича и раствора, а
также указания по армированию, назначаемые в соответствии с требованиями СНиП
II-22-81;
величины минимальной
требуемой прочности раствора швов при различной стадии готовности здания;
предельные высоты
конструкций, которые могут быть допущены в период оттаивания;
конструкции временных
креплений, если они требуются по расчету на период оттаивания.
Примечание. При определении несущей
способности конструкций в стадии оттаивания необходимо учитывать понижающие
коэффициенты, приведенные в п. [7.7].
8.6. В проектах каменных
зданий, возводимых в зимних условиях на обыкновенных (без противоморозных
добавок) растворах, должна быть указана предельно допустимая высота здания.
Прочность оттаявшего раствора принимается равной 0 или 0,2 МПа.
8.7. Противоморозные и
пластифицирующие добавки, рекомендуемые для растворов, приведены в СНиП
III-17-78.
8.8. Выбор противоморозной
добавки должен осуществляться с учетом вида конструкций и условии последующей
их эксплуатации в соответствии с указаниями, приведенными в п. 7.12 СНиП III-17-78.
8.9. Количество
противоморозных добавок в зависимости от среднесуточной температуры наружного
воздуха назначается по указаниям СНиП III-17-78 (прил. 1.).
8.10. Ориентировочная
величина необратимой (сохраняющейся при оттаивании) прочности растворов с
противоморозными добавками, в зависимости от времени их твердения на морозе,
приведена в табл.23.
8.11. Проектная прочность
(марка) растворов с противоморозными добавками, твердеющих при температурах, не
ниже указанных в табл.23 для данного вида
и количества добавки, достигается после оттаивания и твердения при температуре
не ниже 20±5°С и естественной влажности воздуха в течение 28 сут.
Твердение растворов при
температурах, ниже указанных в СНиП III-17-78, приводит к снижению их конечной
прочности, что должно учитываться при назначении марки раствора в соответствии
с п. 8.15.
|
Противоморозные добавки |
Среднесуточная температура
воздуха, °С |
Количество противоморозной
добавки, % массы цемента |
Ожидаемая прочность
раствора, % марки при твердении на морозе в течение суток |
||
|
7 |
28 |
90 |
|||
|
Нитрит натрия (НН) |
От 0 до -2 |
2-3 |
15 |
50 |
70 |
|
„ -3 „ -5 |
4-5 |
10 |
40 |
55 |
|
|
„ -6 „ -15 |
8-10 |
5 |
30 |
40 |
|
|
Поташ (П) |
До -5 |
5 |
25 |
60 |
80 |
|
От -6 до-15 |
10 |
20 |
50 |
65 |
|
|
„ -16 „ -30 |
12 |
10 |
35 |
50 |
|
|
Нитрит натрия + поташ (НН+П) |
„ 0 „ -2 |
1,5+1,5 |
25 |
60 |
80 |
|
„ -3 „ -5 |
2,5+2,5 |
20 |
55 |
75 |
|
|
„ -6 „ -15 |
5+5 |
15 |
40 |
60 |
|
|
„ -16 „ -30 |
6+6 |
5 |
35 |
45 |
|
|
Комплексная добавка (КНМ) |
„ 0 „ -2 |
2-3 |
15 |
50 |
70 |
|
„ -3 „ -5 |
4-5 |
10 |
30 |
50 |
|
|
„ -6 „ -20 |
8-10 |
3 |
20 |
30 |
|
|
Комплексная пластифицированная (НК+ПАЩ-1); (НН +
ПАЩ-1) |
„ 0 „ -5 |
2 |
15 |
50 |
70 |
|
„ -6 „ -15 |
5-6 |
10 |
30 |
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Хлорид натрия + хлорид кальция (ХН+ХК) |
„ 0 „ -5 |
2+0,5 |
30 |
80 |
100 |
|
„ -6 „ -15 |
4+2 |
15 |
35 |
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ННХКМ (готовый продукт + мочевина) |
„ -3 „ -5 |
5 |
30 |
55 |
85 |
|
„ -6 „ -15 |
10 |
20 |
40 |
50 |
|
|
„ -16 „ -30 |
12 |
5 |
20 |
30 |
|
Примечания: 1. В таблице приведены
величины ожидаемой прочности растворов марки 50 и выше, приготовленных на
портландцементе. В случае применения шлакопортландцемента или нитрита натрия в
виде жидкого продукта ожидаемая прочность раствора принимается с коэффициентом
0,8. Если раствор приготовляется на шлакопортландцементе с добавкой нитрита
натрия в виде жидкого продукта, величина ожидаемой прочности принимается с
коэффициентом 0,65.
2. В связи с различной
скоростью твердения растворов с противоморозными добавками, приготовленных на
цементах с различными минералогическими составами, данные таблицы ожидаемой
прочности растворов должны быть предварительно уточнены пробными замесами.
Конечная фактическая прочность раствора в конструкциях должна быть подтверждена результатами испытаний контрольных образцов.
8.12. При возведении зданий
в зимних условиях на растворах с противоморозными добавками должен периодически
проводиться контроль фактической прочности, накопленной раствором за период
твердения. Результаты контроля должны подтверждать наличие требуемой проектом
минимальной прочности раствора.
В случаях, когда по
результатам испытания прочность раствора окажется ниже требуемой для данной
стадии готовности здания, строительные работы должны быть прекращены до набора
им требуемой прочности.
8.13. При возведении зданий
на растворах с противоморозными добавками в проекте производства работ должны
указываться: марка раствора, наименование и количество противоморозных добавок
с учетом вида возводимых конструкций и условий их последующей эксплуатации,
приведенных в СНиП III-17-78.
График производства работ по
возведению здания должен быть увязан со скоростью набора раствором необратимой
прочности, ориентировочная величина которой указана в СНиП III-17-78. Для
обеспечения надежности конструкций при любой стадии готовности здания рост
прочности раствора в швах каменных зданий должен опережать приращение
напряжений от возрастающей нагрузки.
8.14. При возведении зданий
на обыкновенных (без противоморозных добавок) растворах с последующим
упрочнением конструкций искусственным отогреванием в проекте производства работ
необходимо указать число и типы обогревательных приборов, длительность
обогрева, температуру воздуха в обогреваемых помещениях и способы изоляции
обогреваемых помещений от наружного воздуха.
8.15. Марки растворов с
противоморозными добавками назначаются:
равными проектным (летним)
маркам раствора, если каменная кладка будет выполняться при среднесуточной
температуре воздуха не ниже минус 20°С;
на одну марку выше
проектных, если каменная кладка будет выполняться при среднесуточной
температуре воздуха ниже минус 20°С.
Не требуется повышать марки
растворов в конструкциях, работающих с неполным использованием расчетной
несущей способности, например, в верхних этажах зданий при соответствующем
обосновании расчетом. В случае необходимости повышения несущей способности
отдельных каменных конструкций, выполняемых в зимних условиях, допускается
взамен повышения маркий раствора применять кирпич повышенной марки или
армирование при соответствующем обосновании.
8.16. Мероприятия,
обеспечивающие необходимую конечную прочность конструкций, возводимых в зимних
условиях (повышение марок раствора, применение кирпича и камней повышенной
прочности или в отдельных случаях применение сетчатого армирования), должны
указываться в рабочих чертежах. При кладке, выполняемой на растворах с
химическими добавками, указанные мероприятия применяются для элементов кладки,
несущая способность которых используется более чем на 90%;
при кладке, выполняемой
способом замораживания, - для элементов, несущая способность которых
используется более чем на 70%.
8.17. При расчете несущей способности
конструкций, возводимых способом замораживания на обыкновенных (без
противоморозных добавок) растворах, должны производиться:
основной расчет для
законченного здания по истечении 28 сут. после оттаивания и твердения при
температуре не ниже 20±5°С и естественной влажности воздуха;
дополнительная проверка
несущей способности конструкций на период оттаивания. Расчетная прочность
раствора в этом случае принимается равной 0,2 МПа (2 кгс/см2) при
растворе на портландцементе и толщине стен и столбов 38 см и более. При
применении шлакопортландцемента, пуццолановых портландцементов или толщине стен
и столбов менее 38 см расчетная прочность раствора принимается равной нулю.
8.18. Способом замораживания
на обыкновенных (без противоморозных добавок) растворах не допускается
возводить конструкции, перечисленные в п. [7.10].
8.19. Отношение высот стен,
столбов и других каменных конструкций, выполненных способом замораживания на
обыкновенных (без противоморозных добавок) растворах, к их толщине должно
удовлетворять требованиям IV группы кладок, пп. [6.17-6.19]. Для конструкций,
не имеющих верхней опоры, предельные отношения следует уменьшить в 2 раза и
принимать b£6.
8.20. В случае превышения
предельно допустимой гибкости, конструкции должны временно, на период оттаивания,
укрепляться:
подкосами и растяжками,
связывающими стены и столбы между собой;
хомутами, схватывающими
простенки или столбы и прикрепляющими их к элементам каркаса или другим жестким
конструкциям.
Временные крепления должны
сохраняться до набора раствором необходимой по расчету прочности.
8.21. Расчет несущей
способности конструкций, выполненных способом замораживания и упрочненных
искусственным отогреванием, следует производить на период оттаивания с учетом
упрочнения, достигнутого раствором в пределах всего или части сечения.
8.22. При отогревании кладки со
стороны внутренних помещений прочность кладки внутренних стен, отогретых с двух
сторон, или внутренних столбов, отогретых с четырех сторон, определяется
расчетом в соответствии с фактической прочностью раствора. Прочность раствора в
зависимости от средней температуры и длительности периода обогрева помещений,
не включающего в себя период оттаивания стен, который принимается
ориентировочно равным 3 сут., устанавливается по табл. 1.
8.23. Расчетное
сопротивление при центральном сжатии кладки наружных стен, отогреваемых с одной
внутренней стороны, в зависимости от глубины оттаивания и прочности раствора на
внутренней грани стены, достигнутых за период оттаивания, определяется по
формуле
Ry=R0w¢, (120)
где Rу - расчетное сопротивление
зимней кладки наружных стен сжатию, упрочненной односторонним отогреванием;
R0
- расчетное сопротивление сжатию зимней оттаявшей кладки на растворе нулевой
прочности;
w¢ - коэффициент упрочнения
кладки наружных стен, подвергающихся одностороннему отогреванию, определяемый
по табл. 24.
|
Прочность отогретого
раствора на внутренней грани наружной стены, МПа |
Значение коэффициента w¢ при глубине оттаивания
наружных стен, % толщины |
||
|
20-39 |
40-59 |
60 и более |
|
|
0,2 |
1 |
1,05 |
1,2 |
|
0,4 |
1 |
1,05 |
1,2 |
|
1,0 |
1,05 |
1,1 |
1,3 |
|
1,5 |
1,1 |
1,2 |
1,5 |
|
2,5 |
1,15 |
1,4 |
1,7 |
|
5,0 |
1,2 |
1,6 |
1,9 |
Примечания: 1. Коэффициент упрочнения
для кладки на растворе с применением шлакопортландцемента или пуццолановых
портландцементов принимается равным ![]()
2. Прочность отогретого
раствора на внутренней грани наружной стены определяется лабораторными
испытаниями.
8.24. Расчет несущей
способности внецентренно сжатых каменных стен, возведенных способом
замораживания и упрочненных односторонним искусственным отогреванием,
производится:
при эксцентриситетах
приложения силы в сторону отогреваемой части стены - как для центрально сжатых
конструкций;
при эксцентриситетах в сторону
неотогретой части стены - как внецентренно сжатых конструкций с
эксцентриситетом относительно центра тяжести всего сечения конструкции. При
этом величина эксцентриситета допускается не более е0£0,25у.
Коэффициенты продольного
изгиба для стен, отогретых с одной стороны для стадии последующего
естественного оттаивания, принимаются:
при глубине искусственного
оттаивания менее 30% толщины стены - как для кладки на растворе, прочность
которого определяется по указаниям п. 8.22
- в зависимости от общей толщины стены и марки примененного раствора;
при глубине искусственного
оттаивания более 30% толщины стены - как для кладки на растворе средней
прочности, достигнутой при оттаивании.
Примечание. Средняя прочность раствора
при отогревании определяется как полусумма прочности раствора на внутренней
грани стены, определяемой по табл. 24 и прочности раствора в стадии оттаивания по
указаниям п. 8.17.
8.25. Глубина оттаивания при
одностороннем отогревании наружных кирпичных стен в зависимости от величины
средних температур наружного и внутреннего (нагретого) воздуха, а также
длительности отогревания приближенно определяется по указаниям СНиП III-17-78.
8.26. При проектировании зданий с наружными стенами облегченной кладки следует предусматривать их возведение в зимних условиях на растворе с противоморозными химическими добавками. Способом замораживания на обыкновенных (без противоморозных добавок) растворах допускается возводить не более одного этажа при условии, если пространство между наружным и внутренним рядами будет заполняться плитным утеплителем.
8.27. При
оттаивании кладка, выполненная способом замораживания на обыкновенных (без
противоморозных добавок) растворах, дает осадку, равную примерно 1 мм на 1 м
высоты.
В связи с этим в оконных и
дверных проемах над коробками следует предусматривать дополнительный осадочный
зазор шириной не менее 5 мм.
8.28. При проектировании
самонесущих каменных стен и заполнений в каркасных зданиях необходимо
предусматривать их крепление к вертикальным элементам каркаса гибкими связями,
обеспечивающими возможность свободной осадки стен. Расстояние между связями по
высоте не должно превышать 1,5 м.
8.29. При
проектировании стен с облицовками, возведение которых будет осуществляться в
зимних условиях, следует руководствоваться указаниями «Рекомендаций по методике
расчета, проектированию и применению панельных и кирпичных стен с различными
видами облицовок». - М.: ЦНИИСК, 1983.
8.30. В местах опирания
висячих стен, перемычек пролетом свыше 2,5 м и других конструкций, вызывающих
по расчету в период оттаивания перегрузку кладки, необходимо своевременно, до
наступления потепления, предусматривать разгрузку перегруженных опорных
участков кладки временными деревянными стойками. Нагрузки на перемычки следует
принимать в соответствии с пп. [6.47 и 6.53].
Для возможности регулирования
величины осадки кладки опорных конструкций стойки следует устанавливать на
клиньях.
ПРИЛОЖЕНИЕ 1
ПЕРЕЧЕНЬ
ГОСУДАРСТВЕННЫХ СТАНДАРТОВ, НОРМАТИВНЫХ И СПРАВОЧНЫХ
ДОКУМЕНТОВ ПО КАМЕННЫМ КОНСТРУКЦИЯМ, МАТЕРИАЛАМ,
ИЗДЕЛИЯМ, РАСТВОРАМ, ОТДЕЛОЧНЫМ И ТЕПЛОИЗОЛЯЦИОННЫМ
МАТЕРИАЛАМ, ДЕЙСТВУЮЩИХ НА 1 ЯНВАРЯ 1987 г.
1. ГОСУДАРСТВЕННЫЕ СТАНДАРТЫ
ГОСТ
4.206-83 Строительство.
Материалы стеновые каменные. Номенклатура показателей.
ГОСТ 125-86 Вяжущие
гипсовые. Технические условия.
ГОСТ 379-79 Кирпич и
камни силикатные. Технические условия.
ГОСТ 530-80 Кирпич и
камни керамические. Технические условия.
ГОСТ
948-84 Перемычки
железобетонные для зданий с кирпичными стенами. Технические условия.
ГОСТ 965-78 Портландцемент
белый. Технические условия.
ГОСТ 2544-76 Вещества
известьсодержащие гидравлические.
ГОСТ 4001-84 Камни стеновые из горных пород.
Технические условия.
ГОСТ 4640-84 Вата
минеральная. Технические условия.
ГОСТ 4861 -74 Плиты
торфяные теплоизоляционные.
ГОСТ 5578-76 Щебень из
доменного шлака для бетона. Технические условия.
ГОСТ 5742-76 Изделия из ячеистых бетонов
теплоизоляционные.
ГОСТ
5781-82 Сталь горячекатаная
для армирования железобетонных конструкций.
ГОСТ 5802-86 Растворы строительные. Методы
испытаний.
ГОСТ 6133-84 Камни бетонные стеновые.
ГОСТ 6141-82 Плитки
керамические глазурованные для внутренней облицовки стен. Технические условия.
ГОСТ 6427-75 Материалы
стеновые и облицовочные. Методы определения прочности.
ГОСТ 6428-83 Плиты гипсовые для перегородок.
ГОСТ 6927-74 Плиты бетонные фасадные. Технические
требования.
ГОСТ 7025-78 Материалы
стеновые и облицовочные. Методы определения водопоглощения и морозостойкости.
ГОСТ 7076-78 Материалы
строительные. Методы определения теплопроводности.
ГОСТ 7484-78 Кирпич и камни керамические лицевые.
Технические условия.
ГОСТ 8267-82 Щебень из
естественного камня для строительных работ.
ГОСТ
8426-75 Кирпич глиняный для
дымовых труб.
ГОСТ
8462-85 Материалы стеновые и
облицовочные. Методы определения пределов прочности при сжатии и изгибе.
ГОСТ 8735-75 Песок
строительный. Методы испытаний.
ГОСТ 8736-85 Песок для
строительных работ. Технические условия.
ГОСТ 8928-81 Плиты
фибролитовые на портландцементе. Технические условия.
ГОСТ 9179-77 Известь строительная. Технические
условия.
ГОСТ
9479-84 Блоки из природного
камня для производства облицовочных изделий. Технические условия.
ГОСТ 9480-77 Плиты
облицовочные пиленые из природного камня. Технические условия.
ГОСТ 9574-80 Панели
гипсобетонные для перегородок. Технические условия.
ГОСТ
9573-82 Плиты и маты
теплоизоляционные из минеральной ваты на синтетическом связующем. Технические
условия.
ГОСТ 9760-75 Щебень и
песок пористые из металлургического шлака (шлаковая пемза).
ГОСТ
10140-80 Плиты
теплоизоляционные из минеральной ваты на битумном связующем. Технические
условия.
ГОСТ
10178-85 Портландцемент и
шлакопортландцемент. Технические условия.
ГОСТ 10180-78 Бетоны.
Методы определения прочности на сжатие и растяжение.
ГОСТ 10832-83 Песок и
щебень перлитовые вспученные.
ГОСТ 12730.1-78 Бетоны. Метод определения плотности.
ГОСТ 12852.0-77 Бетон ячеистый. Методы испытаний. ГОСТ
12852.6-77
ГОСТ 13579-78 Блоки бетонные для стен подвалов.
Технические условия.
ГОСТ
13580-85 Плиты ленточных
фундаментов железобетонные. Технические условия.
ГОСТ 13996-84 Плитки
керамические фасадные и ковры из них. Технические условия.
ГОСТ 15588-70* Плиты
теплоизоляционные из пенопласта полистирольного.
ГОСТ 15884-85 Блоки
стеновые из природного камня. Технические условия.
ГОСТ 17057-80 Плитки
стеклянные облицовочные коврово-мозаичные и ковры из них. Технические условия.
ГОСТ 18623-82 Плитки
керамические литые и ковры из них.
ГОСТ
19010-82 Блоки из легких
бетонов для наружных стен зданий. Технические условия.
ГОСТ 20916-75 Плиты
теплоизоляционные из пенопласта на основе резольных фенолоформальдегидных смол.
ГОСТ 21520-76 Блоки из
ячеистых бетонов стеновые мелкие.
ГОСТ 21521-76 Изделия
перлитокерамические теплоизоляционные.
ГОСТ 22132-76 Камень
бутовый. Технические условия.
ГОСТ
22546-77 Изделия
теплоизоляционные из пенопласта марок ФРП-1 и Резопен. Технические условия.
ГОСТ 22951-78 Материалы
каменные стеновые. Классификация и общие технические требования.
ГОСТ 22688-77 Известь строительная. Методы испытаний.
ГОСТ 24332-80 Кирпич и
камни силикатные. Ультразвуковой метод определения прочности при сжатии.
ГОСТ
24594-81 Панели и блоки
стеновые из кирпича и керамических камней.
ГОСТ
24992-81 Конструкции каменные.
Метод определения прочности сцепления в каменной кладке.
ГОСТ 25485-82 Бетоны
ячеистые. Технические условия.
2. СТРОИТЕЛЬНЫЕ НОРМЫ И
ПРАВИЛА
СНиП II-22-81 Каменные и
армокаменные конструкции.
СНиП 3-17-78 Каменные
конструкции. Правила производства и приемки работ.
СНиП 2.03.01-84 Бетонные и железобетонные конструкции.
СНиП II-3-79 Строительная
теплотехника.
СНиП
2.01.07-85 Нагрузки и воздействия.
СНиП 3-21-73 Отделочные
покрытия строительных конструкций.
СНиП II-7-81 Строительство
в сейсмических условиях.
СНиП II-12-77 Защита от
шума.
3. НОРМАТИВНЫЕ И СПРАВОЧНЫЕ
ДОКУМЕНТЫ
СН
290-74 Инструкция по
приготовлению и применению строительных растворов.
Пособие по проектированию
бетонных и железобетонных конструкций из ячеистых бетонов (к СНиП
2.03.01-84).-М.: ЦИТП, 1986.
Руководство
по проектированию, изготовлению и применению кирпичных и керамических панелей в
строительстве зданий. - М.: Стройиздат, 1977.
Временные рекомендации по
заводскому изготовлению крупных виброкирпичных блоков и панелей. - М.: ЦНИИСК,
1980.
Типовые конструкции и детали
зданий и сооружений. Серия 2.130-1. Детали стен и перегородок жилых зданий. -
Вып. 1. Кирпичные стены сплошной кладки. - М.: ЦИТП, 1970.
Типовая документация на
строительные системы и изделия зданий и сооружений. Серия 2.130-1. Детали стен
и перегородок жилых зданий. - Вып. 23. Наружные кирпичные и каменные стены
облегченной кладки. Материалы для проектирования и рабочие чертежи. - М.: ЦИТП,
1982.
Руководство по проектированию
и возведению каменных сводов двоякой кривизны. - М.: Стройиздат, 1976.
Рекомендации по методике
расчета, проектированию и применению панельных и кирпичных стен с различными
видами облицовок. - М.: Стройиздат, 1983.
Рекомендации по усилению
каменных конструкций зданий и сооружений. - М.: Стройиздат, 1984.
ПРИЛОЖЕНИЕ 2
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИСКУССТВЕННЫХ СТЕНОВЫХ МАТЕРИАЛОВ, ПРИМЕНЯЕМЫХ В СТРОИТЕЛЬСТВЕ
|
Изделие |
Нормативный документ |
Размеры изделий, мм (длина´ширина´высота) |
Марка по прочности или
плотности |
Плотность, кг/м3 |
Морозостойкость, Мрз, не
ниже |
Коэффициент
теплопроводности, Вт/(м×К) [ккал/(м×ч×град)], для условий
эксплуатации |
|
||||||||
|
материала |
кладки |
||||||||||||||
|
А |
Б |
|
|||||||||||||
|
I. КЛАДКА ИЗ КАМНЕЙ
КЕРАМИЧЕСКИХ И БЕТОННЫХ |
|
||||||||||||||
|
Камни керамические пустотелые стеновые
пластического прессования: |
ГОСТ 530-80 |
250´120´138 |
250, 200, 175, 150, 125,
100 и 75 |
|
|
|
|
|
|
||||||
|
с 7 или 18 пустотами |
|
|
|
1460-1600 |
1600-1650 |
15 |
0,58 (0,50) |
0,64 (0,55) |
|
||||||
|
с 21 или 28 пустотами |
|
|
|
1300 |
1400 |
|
0,52 (0,45) |
0,58 (0,50) |
|
||||||
|
Камни керамические лицевые пустотелые |
250´120´138 |
300, 250, 200, 175, 150,
125 и 100 |
1400 |
1470 |
25 |
0,52 (0,45) |
0,58 (0,50) |
|
|||||||
|
Камни силикатные: |
ГОСТ 379-79 |
250´120´138 |
|
|
|
|
|
|
|
||||||
|
рядовые |
250, 200, 150, 125, 100 и
75 |
1400 |
1450 |
15 |
0,64 (0,55) |
0,76 (0,65) |
|
||||||||
|
1550 |
1600 |
|
0,70 (0,60) |
0,81 (0,70) |
|
||||||||||
|
лицевые |
300, 250, 200, 150, 125 и
100 |
1400 |
1450 |
25 |
0,64 (0,55) |
0,76 (0,65) |
|
||||||||
|
1550 |
1600 |
|
0,70(0,60) |
0,81 (0,70) |
|
||||||||||
|
Камни из ячеистых бетонов |
ГОСТ 21520-76 |
588´(200, 250, 300) ´ ´(188, 288) |
150, 100, 75, 50, 35 и 25 |
600 |
720 |
25 |
0,22 (0,19) |
0,26 (0,22) |
|
||||||
|
800 |
900 |
|
0,33 (0,28) |
0,37 (0,32) |
|
||||||||||
|
588´(200, 250, 300)´88 |
1000 |
1100 |
|
0,41 (0,35) |
0,46 (0,40) |
|
|||||||||
|
Камни бетонные: |
|
|
|
|
|
|
|
|
|||||||
|
со щелевидными пустотами |
390´190´188 390´90´188 |
200, 150, 100, 75, 50, 35 и
25 |
1100 |
- |
15 |
- |
0,43 (0,37) |
|
|||||||
|
1300 |
- |
|
- |
0,52 (0,45) |
|
||||||||||
|
1600 |
- |
|
- |
0,70 (0,60) |
|
||||||||||
|
1200 |
- |
|
- |
0,50 (0,43) |
|
||||||||||
|
1450 |
- |
|
- |
0,59 (0,51) |
|
||||||||||
|
1750 |
- |
|
- |
0,83 (0,71) |
|
||||||||||
|
трехпустотные со сквозными
пустотами |
390´190´188 |
75, 50, 35 и 25 |
900 |
- |
|
- |
0,71 (0,61) |
|
|||||||
|
1100 |
- |
|
- |
0,80 (0,69) |
|
||||||||||
|
1900 |
- |
|
- |
0,97 (0,83) |
|
||||||||||
|
II. КЛАДКА ИЗ КИРПИЧА |
|
||||||||||||||
|
Кирпич глиняный пустотелый пластического
прессования: |
ГОСТ 530-80 |
|
|
|
|
|
|
|
|
||||||
|
с 13 пустотами |
250´120´88; 250´120´65 |
150, 125, 100 и 75 |
1500 |
1600 |
15 |
0,58 (0,50) |
0,64 (0,55) |
|
|||||||
|
с 19 и 32 пустотами |
250´120´88; |
150, 125, 100 и 75 |
1300 |
1400 |
|
0,52 (0,45) |
0,58 (0,50) |
|
|||||||
|
250´120´65 |
1000 |
1200 |
|
0,47 (0,40) |
0,52 (0,45) |
|
|||||||||
|
с 28 пустотами |
250´120´88; 250´120´65 |
150, 125, 100 и 75 |
1300 |
1400 |
|
0,52 (0,45) |
0,58 (0,50) |
|
|||||||
|
Кирпич пустотелый полусухого прессования |
ГОСТ 530-80 |
250´120´88; 250´120´65 |
200, 175, 150, 125, 100 и
75 |
1500 |
1600 |
15 |
0,70 (0,60) |
0,84 (0,70) |
|
||||||
|
Кирпич легковесный (глиняный пористый, трепельный) |
ГОСТ 530-80 |
250´120´65 |
200, 150, 125, 100 и 75 |
700 |
950 |
15 |
0,35 (0,30) |
0,41 (0,35) |
|
||||||
|
800 |
1000 |
|
0,41 (0,35) |
0,44 (0,38) |
|
||||||||||
|
1000 |
1200 |
|
0,47 (0,40) |
0,52 (0,45) |
|
||||||||||
|
1200 |
1350 |
|
0,52 (0,45) |
0,58 (0,50) |
|
||||||||||
|
1400 |
1500 |
|
0,64 (0,55) |
0,70 (0,60) |
|
||||||||||
|
Кирпич глиняный обыкновенный: |
ГОСТ 530-80 |
|
|
|
|
|
|
|
|
||||||
|
пластического прессования |
250´120´65 |
300, 250, 200, 175, 150,
125, 100 и 75 |
1750 |
1800 |
15 |
0,70 (0,60) |
0,81 (0,70) |
|
|||||||
|
полусухого прессования |
250´120´65 |
200, 150, 125, 100 и 75 |
1750 |
1800 |
|
0,70 (0,60) |
0,81 (0,70) |
|
|||||||
|
Кирпич силикатный: |
ГОСТ 379-79 |
|
|
|
|
|
|
|
|
||||||
|
рядовой |
|
250´120´88; |
250, 200, 150, 125, 100 и
75 |
1600 |
1700 |
15 |
0,70 (0,60) |
0,81 (0,70) |
|
||||||
|
|
250´120´65 |
1750 |
1800 |
|
0,76 (0,65) |
0,87 (0,75) |
|
||||||||
|
лицевой |
250´120´88; 250´120´65 |
300, 250, 200, 150 и 125 |
1600 1750 |
1700 1800 |
25 |
0,70 (0,60) 0,76(0,65) |
0,81 (0,70) 0,87 (0,75) |
|
|||||||
|
III. ГРУНТОВЫЕ МАТЕРИАЛЫ |
|
||||||||||||||
|
Грунтобетонные камни |
- |
250´125´140 |
75, 50, 35 и 25 |
- |
1800 |
- |
- |
0,81 (0,70) |
|
||||||
|
|
- |
2000 |
- |
- |
0,93 (0,80) |
|
|||||||||
|
Грунтобетон |
- |
- |
75, 50 и 35 |
- |
1600 1800 |
- |
- |
0,72 (0,62) 0,81 (0,70) |
|
||||||
|
Саман |
- |
- |
25, 15 и 10 |
- |
1600 |
- |
0,58 (0,50) |
0,70 (0,60) |
|
||||||
|
IV. МАТЕРИАЛЫ, ПРИМЕНЯЕМЫЕ
ДЛЯ ТЕПЛОИЗОЛЯЦИИ |
|
||||||||||||||
|
Легкие бетоны: |
|
|
|
|
|
|
|
|
|||||||
|
керамзитобетон |
- |
10-50 |
500 |
- |
- |
0,17 (0,15) |
0,23 (0,20) |
|
|||||||
|
|
|
600 |
- |
- |
0,20 (0,17) |
0,26 (0,22) |
|
||||||||
|
|
|
800 |
- |
- |
0,24 (0,21) |
0,31 (0,27) |
|
||||||||
|
|
|
1000 |
- |
- |
0,33 (0,28) |
0,41 (0,35) |
|
||||||||
|
|
|
1200 |
- |
- |
0,44 (0,38) |
0,52 (0,45) |
|
||||||||
|
|
|
1400 |
- |
- |
0,56 (0,48) |
0,65 (0,56) |
|
||||||||
|
|
|
1600 |
- |
- |
0,67 (0,58) |
0,79 (0,68) |
|
||||||||
|
перлитобетон |
- |
10-25 |
600 |
- |
- |
0,19 (0,16) |
0,23 (0,20) |
|
|||||||
|
|
|
800 |
- |
- |
0,27 (0,23) |
0,33 (0,28) |
|
||||||||
|
|
|
1000 |
- |
- |
0,33 (0,28) |
0,38 (0,33) |
|
||||||||
|
|
|
1200 |
- |
- |
0,44 (0,38) |
0,50 (0,43) |
|
||||||||
|
бетон на аглопорите и
топливных шлаках |
- |
10-50 |
800 |
- |
- |
0,29 (0,25) |
0,35 (0,30) |
|
|||||||
|
|
|
1000 |
- |
- |
0,38 (0,33) |
0,44 (0,38) |
|
||||||||
|
|
|
1200 |
- |
- |
0,48 (0,41) |
0,53 (0,46) |
|
||||||||
|
|
|
1400 |
- |
- |
0,59 (0,51) |
0,65 (0,56) |
|
||||||||
|
|
|
1600 |
- |
- |
0,72 (0,62) |
0,78 (0,67) |
|
||||||||
|
|
|
1800 |
- |
- |
0,85 (0,73) |
0,93 (0,80) |
|
||||||||
|
шлакобетон на доменных
гранулированных шлаках |
- |
10-50 |
1200 |
- |
- |
0,47 (0,40) |
0,52 (0,45) |
|
|||||||
|
|
|
1400 |
- |
- |
0,52 (0,45) |
0,58 (0,50) |
|
||||||||
|
|
|
1600 |
- |
- |
0,58 (0,50) |
0,64 (0,55) |
|
||||||||
|
|
|
1800 |
- |
- |
0,70 (0,60) |
0,81 (0,70) |
|
||||||||
|
Плиты гипсовые с органическими заполнителями |
- |
35-50 |
1100 |
- |
- |
0,17 (0,15) |
0,20 (0,17) |
|
|||||||
|
|
|
1350 |
- |
- |
0,21 (0,18) |
0,23 (0,20) |
|
||||||||
|
Панели гипсобетонные |
ГОСТ 9574-80 |
- |
50 |
1100 |
- |
- |
0,35 (0,30) |
0,41 (0,35) |
|
||||||
|
|
|
1500 |
- |
- |
0,41 (0,35) |
0,47 (0,40) |
|
||||||||
|
Плиты гипсобетонные: |
|
|
|
|
|
|
|
|
|||||||
|
на доменных гранулированных
шлаках |
- |
- |
1000 |
- |
- |
0,33 (0,28) |
0,37 (0,32) |
|
|||||||
|
на топливных шлаках |
- |
- |
1300 |
- |
- |
0,47 (0,40) |
0,56 (0,48) |
|
|||||||
|
Плиты из ячеистого бетона |
1000´500´ (80-200) |
Не менее 12, 8 |
Марка А400 |
- |
- |
0,13 (0,11) |
0,14 (0,12) |
|
|||||||
|
|
|
Б500 |
- |
- |
0,16 (0,14) |
0,17 (0,15) |
|
||||||||
|
Минеральная вата |
ГОСТ 4640-84 |
- |
- |
150 |
- |
- |
0,046 (0,040) |
0,049 (0,042) |
|
||||||
|
|
|
200 |
|
|
0,051 (0,044) |
0,055 (0,047) |
|
||||||||
|
То же, уплотненная в стене |
- |
- |
400 |
- |
- |
0,093 (0,080) |
0,12 (0,1) |
|
|||||||
|
Изделия минераловатные на битумной связке: |
(1000-2000)´(500-1000)´(50, 60, 70, 80 и 100) |
|
|
|
|
|
|
|
|||||||
|
плиты мягкие и полужесткие |
- |
75 |
- |
- |
0,044 (0,038) |
0,046 (0,040) |
|
||||||||
|
|
100 |
- |
- |
0,044 (0,038) |
0,046 (0,040) |
|
|||||||||
|
|
150 |
- |
- |
0,049 (0,042) |
0,052 (0,045) |
|
|||||||||
|
|
200 |
- |
- |
0,052 (0,045) |
0,058 (0,050) |
|
|||||||||
|
|
250 |
- |
- |
0,058 (0,050) |
0,064 (0,055) |
|
|||||||||
|
плиты жесткие |
- |
300 |
- |
- |
0,087 (0,075) |
0,093 (0,080) |
|
||||||||
|
|
400 |
- |
- |
0,084 (0,072) |
0,087 (0,075) |
|
|||||||||
|
Изделия минераловатные на синтетическом связующем: |
ГОСТ
9573-82 |
1000´(500, 1000)´(40, 50, 60, 70, 80) |
|
|
|
|
|
|
|
||||||
|
маты рулонные |
|
|
50 |
50 |
- |
- |
0,052 (0,045) |
0,058 (0,050) |
|
||||||
|
|
|
75 |
75 |
- |
- |
0,058 (0,050) |
0,064 (0,055) |
|
|||||||
|
плиты мягкие, жесткие и
полужесткие |
|
|
125 |
125 |
- |
- |
0,064 (0,055) |
0,070 (0,060) |
|
||||||
|
|
|
175 |
175 |
- |
- |
- |
0,064 (0,055) |
|
|||||||
|
|
|
200 |
200 |
- |
- |
- |
0,056 (0,048) |
|
|||||||
|
|
|
300 |
300 |
- |
- |
- |
0,060 (0,052) |
|
|||||||
|
Фибролит на портландцементе |
ГОСТ 8928-81 |
(2400, 3000)´(600, 1200)´(30, 50, 75, 100, 150) |
- |
300 |
- |
- |
0,10 (0,09) |
0,14 (0,12) |
|
||||||
|
|
400 |
- |
- |
0,13 (0,11) |
0,16 (0,14) |
|
|||||||||
|
|
500 |
- |
- |
0,15 (0,13) |
0,21 (0,18) |
|
|||||||||
|
|
600 |
- |
- |
0,17 (0,15) |
0,23 (0,20) |
|
|||||||||
|
Плиты камышитовые |
- |
(2400, 2600, 2800)´(550, 950, 1150, 1500)´(30, 50, 70, 100) |
- |
200 |
- |
- |
0,07 (0,06) |
0,093 (0,08) |
|
||||||
|
|
|
|
300 |
- |
- |
0,093 (0,08) |
0,14 (0,12) |
|
|||||||
|
Минеральные засыпки: |
|
|
|
|
|
|
|
|
|
||||||
|
шлаки топливные |
- |
- |
- |
700 |
- |
- |
0,17 (0,15) |
0,22 (0,19) |
|
||||||
|
|
|
|
|
1000 |
- |
- |
0,23 (0,20) |
0,29 (0,25) |
|
||||||
|
шлаки доменные
гранулированные |
- |
- |
- |
500 700 |
- - |
- - |
0,14 (0,12) 0,17 (0,15) |
0,16 (0,14) 0,22 (0,19) |
|
||||||
|
природная пемза или туф
(засыпки) |
|
|
|
900 |
- |
- |
0,21(0,18) |
0,26 (0,22) |
|
||||||
|
|
|
|
1000 |
- |
- |
0,23 (0,20) |
0,29 (0,25) |
|
|||||||
|
- |
- |
- |
400 |
- |
- |
0,14 (0,12) |
0,17 (0,15) |
|
|||||||
|
|
|
|
600 |
- |
- |
0,17 (0,15) |
0,23 (0,20) |
|
|||||||
|
щебень из доменного шлака |
ГОСТ 5578-76 |
- |
- |
500 |
- |
15 |
0,14 (0,12) |
0,16 (0,14) |
|
||||||
|
|
|
900 |
- |
|
0,21 (0,18) |
0,26 (0,22) |
|
||||||||
|
пемза шлаковая |
ГОСТ 9760-75 |
- |
- |
400 |
- |
15 |
0,14 (0,12) |
0,16 (0,14) |
|
||||||
|
|
|
600 |
- |
|
0,17 (0,15) |
0,21 (0,18) |
|
||||||||
|
|
|
800 |
- |
|
0,21 (0,18) |
0,26 (0,22) |
|
||||||||
|
гравий керамзитовый |
ГОСТ 9759-76 |
- |
- |
300 |
- |
15 |
0,13 (0,11) |
0,15 (0,13) |
|
||||||
|
|
|
500 |
- |
|
0,17 (0,15) |
0,21 (0,18) |
|
||||||||
|
|
|
800 |
- |
|
0,35 (0,30) |
0,41 (0,35) |
|
||||||||
|
перлит вспученный |
ГОСТ 10832-74 |
- |
- |
75 |
- |
15 |
0,047 (0,040) |
- |
|
||||||
|
|
|
100 |
- |
|
0,052 (0,045) |
- |
|
||||||||
|
|
|
150 |
- |
|
0,058 (0,050) |
- |
|
||||||||
|
|
|
200 |
- |
|
0,064 (0,055) |
- |
|
||||||||
|
|
|
250 |
- |
|
0,070 (0,060) |
- |
|
||||||||
|
|
|
300 |
- |
|
0,076 (0,065) |
- |
|
||||||||
|
|
|
400 |
- |
|
0,081 (0,070) |
- |
|
||||||||
|
|
|
500 |
- |
|
0,093 (0,080) |
- |
|
||||||||
|
песок сухой |
ГОСТ 8736-85 |
- |
- |
1700 |
- |
|
0,46 (0,40) |
0,58 (0,50) |
|
||||||
|
|||||||||||||||
ПРИЛОЖЕНИЕ 3
ПЛОТНОСТЬ И ПРЕДЕЛЫ ПРОЧНОСТИ ПРИРОДНЫХ КАМНЕЙ ИЗ ГОРНЫХ ПОРОД
|
Вид камня |
Плотность, кг/м3 |
Предел прочности, МПа |
Наиболее распространенные
марки камня |
|
|
от |
до |
|||
|
Известняк плотный, прочный |
2000-2600 |
15 |
200 |
200, 300, 400, 600 |
|
Мрамор |
2500-2800 |
100 |
300 |
1000 |
|
Песчаник |
2100-2800 |
10 |
200 |
300, 400, 500, 600, 800 |
|
Гранит |
2500-2800 |
100 |
320 |
1000 |
|
Сиенит |
2500-2900 |
150 |
200 |
1000 |
|
Диабаз |
3000 |
200 |
400 |
1000 |
|
Базальт |
2700-3300 |
100 |
400 |
1000 |
|
Вулканические туфы: |
|
|
|
|
|
артикский (Армянская ССР) |
900-1500 |
3,5 |
15 |
35, 75, 100 |
|
тедзамский (Грузинская ССР) |
1200 |
9,0 |
15 |
50, 75, 100 |
|
Известняки пильные малой прочности: |
|
|
|
|
|
крымский желтый
(евпаторийский) |
900-1200 |
0,4 |
1,5 |
4, 7, 10 |
|
крымский белый (керченский) |
1200-1400 |
0,7 |
2,5 |
7, 10, 15 |
|
одесский |
1100-1300 |
0,7 |
1,5 |
7, 10, 15 |
|
молдавский |
1400-1600 |
1,5 |
5,0 |
15, 25, 35 |
|
бакинский: |
|
|
|
|
|
пористый |
1300-1400 |
0,7 |
1,5 |
7, 10, 15 |
|
более плотный |
1500-2000 |
2,5 |
15 |
35, 50, 75, 100, 150 |
|
Мел |
1300-1900 |
1,5 |
7,5 |
15, 25, 35, 50 |
ПРИЛОЖЕНИЕ 4
ВЯЖУЩИЕ И СОСТАВЫ РАСТВОРОВ
1. Выбор вяжущих для
приготовления раствора для каменной кладки и заполнения монтажных швов в
крупноблочных и крупнопанельных стенах в летних условиях следует производить по
СН
290-74.
2. Для получения
удобоукладываемых цементных растворов в их состав вводят неорганические
пластификаторы (известь или глину) или органические пластификаторы-микропенообразователи
(мылонафт, подмыльный щелок и др.), а также отходы промышленности (карбидный
ил, цементная пыль и др.).
3. Составы растворов с
применением вяжущих различных видов для зданий со сроком службы 100, 50 и 25
лет приведены в табл. 1
приложения.
4. Расходы вяжущих на 1 м3
песка и 1 м3 раствора приведены в табл. 2 приложения.
5. Расходы вяжущих в
зависимости от требуемого срока службы и влажностных условий, в которых здание
находится во время хксплуатации, должны быть не ниже приведенных в табл. 3.
6. В массовом малоэтажном
строительстве в летних условиях, когда не требуются растворы высоких марок,
следует применять цементно-известковые и цементно-глиняные растворы (табл. 4, 5).
СОСТАВЫ РАСТВОРОВ ПО ОБЪЕМУ С
ПРИМЕНЕНИЕМ ВЯЖУЩИХ РАЗЛИЧНЫХ ВИДОВ
|
Марка вяжущего |
Марка раствора |
|
||||||||||||
|
200 |
150 |
100 |
75 |
50 |
25 |
10 |
4 |
|
||||||
|
Составы
цементно-известковых и цементно-глиняных растворов для надземных и подземных
конструкций |
|
|||||||||||||
|
А.
При относительной влажности воздуха помещений до 60% и для фундаментов в
маловлажных грунтах |
|
|||||||||||||
|
500 |
1:0,2:3 |
1:0,3:4 |
1:0,5:5,5 |
1:0,8:7 |
- |
- |
- |
- |
|
|||||
|
400 |
1:0,1:2,5 |
1:0,2:3 |
1:0,4:4,5 |
1:0,5:5,6 |
1:0,9:8 |
- |
- |
- |
|
|||||
|
300 |
- |
1:0,1:2,5 |
1:0,2:3,5 |
1:0,3:4 |
1:0,6:6 |
1:1,4:10,5 |
- |
- |
|
|||||
|
200 |
- |
- |
- |
1:0,1:2,5 |
1:0,3:4 |
1:0,8:7 |
- |
- |
|
|||||
|
150 |
- |
- |
- |
- |
- |
1:0,3:4 |
1:1,2:9,5 |
- |
|
|||||
|
100 |
- |
- |
- |
- |
- |
1:0,1:2 |
1:0,5:5 |
- |
|
|||||
|
50 |
- |
- |
- |
- |
- |
- |
1:0,1:2,5 |
1:0,7:6 |
|
|||||
|
25 |
- |
- |
- |
- |
- |
- |
- |
1:0,2:3 |
|
|||||
|
Б. При относительной
влажности воздуха помещений свыше 60% и для фундаментов во влажных грунтах |
||||||||||||||
|
500 |
1:0,2:3 |
1:0,3:4 |
1:0.5:5,5 |
1:0,8:7 |
- |
- |
- |
- |
||||||
|
400 |
1:0,1:2,5 |
1:0,2:3 |
1:0,4:4,5 |
1:0,5:5,5 |
1:0,9:8 |
- |
- |
- |
||||||
|
300 |
- |
1:0,1:2,5 |
1:0,2:3,5 |
1:0,3:4 |
1:0,6:6 |
1:1:10,5 1:1:9* |
|
- |
||||||
|
200 |
- |
- |
- |
1:0,1:2,5 |
1:0,3:4 |
1:0,8:7 |
1:1:9 1:0,8:7* |
- |
||||||
|
150 |
- |
- |
- |
- |
- |
1:0,3:4 |
1:0,5:5 |
- |
||||||
|
100 |
- |
- |
- |
- |
- |
1:0,1:2 |
- |
- |
||||||
|
Составы цементных растворов
для фундаментов и других конструкций, расположенных в насыщенных водой
грунтах и ниже уровня грунтовых вод |
||||||||||||||
|
500 |
1:0:3 |
1:0:4 |
1:0:5,5 |
1:3:6 |
- |
- |
- |
- |
||||||
|
400 |
1:0:2,5 |
1:0:3 |
1:0:4,5 |
1:0:5,5 |
- |
- |
- |
- |
||||||
|
300 |
- |
1:0:2,5 |
1:0:3 |
1:0:4 |
1:0:6 |
- |
- |
- |
||||||
|
200 |
|
- |
- |
1:0:2,5 |
1:0:4 |
- |
- |
- |
||||||
* В числителе приведены
составы цементно-известковых растворов, в знаменателе - цементно-глиняных.
Примечание. Составы растворов
установлены с учетом следующих показателей:
объемная масса вяжущих марки
от 200 до 500 .... 1100 кг/м3;
« « « « 150 .......
900 кг/м3;
« « « « от 25 до 100 .... 700 кг/м3;
объемная масса известкового
теста .......... 700 кг/м3;
объемная масса глиняного теста с глубиной погружения в него стандартного
конуса на 130-140 мм;
песок влажностью 3-7 %.
РАСХОД ВЯЖУЩИХ, КГ НА 1 М3
ПЕСКА/РАСТВОРА
|
Марка вяжущего |
Марка раствора |
|||||||
|
200 |
150 |
100 |
75 |
50 |
25 |
10 |
4 |
|
|
500 |
360 410 |
280 330 |
205 245 |
160 195 |
- |
- |
- |
- |
|
400 |
450 490 |
350 400 |
255 300 |
200 240 |
140 175 |
- |
- |
- |
|
300 |
- |
470 510 |
340 385 |
270 310 |
185 225 |
105 135 |
- |
- |
|
200 |
- |
- |
- |
405 445 |
280 325 |
155 190 |
- |
- |
|
150 |
- |
- |
- |
- |
- |
206 240 |
93 110 |
- |
|
100 |
- |
- |
- |
- |
- |
310 330 |
140 165 |
- |
|
50 |
- |
- |
- |
- |
- |
- |
280 320 |
120 145 |
|
25 |
- |
- |
- |
- |
- |
- |
- |
240 270 |
Примечание. Расход вяжущих на 1 м3
песка (числитель) и на 1 м3 раствора (знаменатель) относится к
цементно-известковым и цементно-глиняным растворам. Для растворов без добавок
извести и глины и растворов с добавками органических
пластификаторов-микропенообразователей расход вяжущих устанавливается на
основании лабораторных данных.
МИНИМАЛЬНЫЙ РАСХОД ВЯЖУЩИХ
|
Влажностный режим |
Раствор, кг/м3 |
|
|
цементно-известковый |
цементно-глиняный |
|
|
Помещения сухие (относительная влажность до 60%) и
фундаменты в маловлажных грунтах |
75 |
100 |
|
Влажные помещения (относительная влажность выше
60%) и фундаменты во влажных грунтах |
100 |
125 |
СОСТАВЫ ИЗВЕСТКОВЫХ РАСТВОРОВ
|
Сорт извести |
Состав раствора по объему
(известковое тесто: песок) |
Марка раствора |
||
|
28 сут. |
3 мес. |
6 мес. |
||
|
Воздушная известь: |
|
|
|
|
|
1-го сорта |
1:4,5 |
4 |
4 |
10 |
|
2-го " |
1:4 |
4 |
4 |
10 |
|
Слабая гидравлическая известь |
1:4,5 |
4 |
10 |
10 |
Примечания: 1. Дозировка извести принята
в виде теста объемной массой 1400 кг/м3.
2. Песок принят влажностью 3-7%.
СОСТАВЫ ГЛИНЯНЫХ РАСТВОРОВ
|
Раствор |
Добавки |
Состав раствора по объему
(глина: добавка: песок) |
Марка раствора |
|
|
в сухом климате |
в умеренно-влажном климате |
|||
|
Глиняный: |
|
|
|
|
|
на жирной глине |
Без добавки |
1:0:4 |
10 |
2 |
|
на глине средней жирности |
Тоже |
1:0:3 |
10 |
2 |
|
на тощей глине или суглинке |
« |
1:0:2,5 |
10 |
2 |
|
Глиняный с черными вяжущими |
Черные вяжущие (деготь,
битум, пек) |
1:2,5:4 |
4 |
4 |
Примечания: 1. Глиняные растворы
применяются в летних условиях для надземной кладки преимущественно в сухом
климате при нормальной влажности воздуха помещений.
2. При применении твердых
черных вяжущих предварительно приготовляется эмульсия из глины с черными
вяжущими в подогретом состоянии.
ПРИЛОЖЕНИЕ 5
ГРАФИКИ ДЛЯ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ЦЕНТРА ТЯЖЕСТИ И МОМЕНТОВ ИНЕРЦИИ ТАВРОВЫХ СЕЧЕНИЙ
А. ГРАФИК ДЛЯ ОПРЕДЕЛЕНИЯ
ПОЛОЖЕНИЯ ЦЕНТРА ТЯЖЕСТИ

Б. ГРАФИК ДЛЯ ОПРЕДЕЛЕНИЯ
МОМЕНТОВ ИНЕРЦИИ
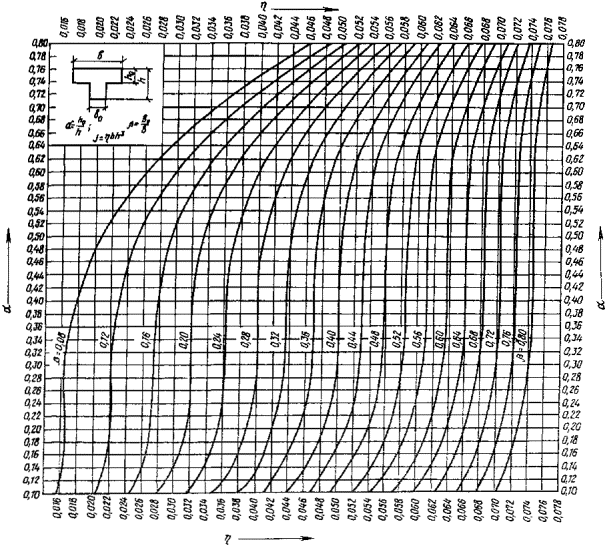
ПРИЛОЖЕНИЕ 6
ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ РАСЧЕТНОЙ
СЖАТОЙ ЧАСТИ ПЛОЩАДИ СЕЧЕНИЯ КЛАДКИ
ПРИ ВНЕЦЕНТРЕННОМ СЖАТИИ
1. В общем случае для сложных
типов внецентренно сжатых поперечных сечений положение границы расчетной сжатой
части сечения определяется из условия равенства нулю статического момента этой
части сечения относительно оси, проходящей через точку приложения сжимающей
силы.
2. Для таврового сечения
расстояние от точки приложения силы до границы расчетной сжатой зоны-с
определяется по формулам:
а) при эксцентриситете в
сторону полки (черт. 1)
Если ![]() , то в сжатую часть будет входить только часть полки,
симметричная относительно точки приложения силы N; в этом случае
, то в сжатую часть будет входить только часть полки,
симметричная относительно точки приложения силы N; в этом случае
x=e1;
Черт. 1. Эксцентриситет в сторону полки
Черт. 2. Эксцентриситет в сторону ребра
б) при эксцентриситете в
сторону ребра (черт. 2)
При ![]() ;
х=e2.
;
х=e2.
Примечание. Для случи больших
эксцентриситетов (е0>0,45у) можно принимать для таврового сечения
приближенно
Ас=2b(у-е0),
где b - ширина сжатой полки или
стенки таврового сечения в зависимости от направления эксцентриситета.
ПРИЛОЖЕНИЕ 7
РАСЧЕТ АРМОКАМЕННЫХ ЭЛЕМЕНТОВ
С ПРОДОЛЬНОЙ АРМАТУРОЙ
ПРИ ВНЕЦЕНТРЕННОМ СЖАТИИ
ОПРЕДЕЛЕНИЕ Sc ПРИ ИЗВЕСТНОМ х
|
Форма сечения |
Схема сечения |
Положение нейтральной оси |
Формулы для определения |
|
|
Произвольная |
|
Между арматурами Аs и Аs¢ |
Sc=Acz, (1) где Ac - площадь сжатой зоны
сечения кладки; z - расстояние от центра
тяжести сжатой зоны сечения кладки до арматуры Аs |
|
|
Прямоугольная |
|
То же |
где b - ширина сечения; х - высота сжатой зоны; h0 - расчетная высота |
|
|
Тавровая |
|
Ось проходит в ребре сечения, полка и часть ребра
сжаты |
где b1 - ширина ребра; S0 - статический момент всего сечения
кладки относительно центра тяжести растянутой или менее сжатой арматуры Аs |
|
|
Тавровая |
|
Ось проходит в полке, часть или вся полка сжата,
ребро в растянутой зоне |
где b - ширина полки |
|
|
Тавровая |
|
Ось проходит в ребре, все ребро или часть сжаты,
полка в растянутой зоне |
||
|
Тавровая |
|
Ось проходят в полке, все ребро и часть полки
сжаты |
||
Примечание. Сжатая зона сечения на
эскизах заштрихована.
1. В табл. 2 приведены основные условия и формулы расчета
прочности внецентренно сжатых элементов с продольной арматурой. Из этих формул
видно, что при внецентренном сжатии в случае 1 (Sс<0,8S0) прочность сечения
обусловливается двумя основными условиями равновесия внешних и внутренних сил:
расчетное усилие N должно быть равно или меньше проекции сил на продольную ось элемента, формулы (7), (9), (11), (13);
сумма моментов относительно
точки приложения продольной расчетной силы N равна нулю, формулы (8), (10). При этом принята
прямоугольная эпюра предельных напряжений в кладке (см. черт. 13). Необходимо также соблюдение условия z£h0-a1.
Условие прочности
внецентренно сжатых элементов в случае 2S³0,8S0, формулы (15)-(20), принято на основании
экспериментально установленной закономерности, что момент, воспринимаемый
кладкой, относительно центра тяжести менее сжатой (растянутой) арматуры Аs не
зависит от эксцентриситета продольной силы e0 (e0 - расстояние от точки
приложения силы N до центра тяжести сечения).
2. При расчете сечений с
продольной арматурой вначале необходимо установить, к какому расчетному случаю
отнести рассматриваемое сечение. Для этого необходимо определить Sc
или х.
При прямоугольной форме
сечения по формуле (12)
при двойном армировании и формуле
(14) при одиночном армировании определяют высоту сжатой зоны х и по условию
Sc<0,8S0 или Sc³0,8S0 устанавливают, к какому
случаю внецентренного сжатия относится выполняемый расчет.
Для непрямоугольной формы
сечения по формулам (8) и (10) определяют статический
момент ScN. Затем по ScN определяют х, по х находят
Sc и по условию Sc<0,8S0 или Sc³0,8S0 устанавливают, к какому
случаю относится рассматриваемый расчет.
3. При проектировании
элементов с продольной арматурой приходится в основном решать следующие задачи:
а) по заданному
эксцентриситету и величине продольной силы N, сечению кладки А и
расчетным сопротивлениям кладки и арматуры подбирать сечение арматуры (табл. 3);
б) по заданному
эксцентриситету продольной силы, площадям сечения кладки А, арматуры As и As¢, расчетным сопротивлениям
кладки R и арматуры Rs проверять расчетную несущую способность
элемента (табл. 4).
ОСНОВНЫЕ ФОРМУЛЫ И УСЛОВИЯ
ДЛЯ РАСЧЕТА ПРОЧНОСТИ ВНЕЦЕНТРЕННО СЖАТЫХ ЭЛЕМЕНТОВ С ПРОДОЛЬНОЙ АРМАТУРОЙ
|
Внецентренное сжатие |
Форма сечения |
Необходимые условия для
расчетного случая |
Основные формулы для
расчета прочности |
|
|
при армировании сечения
двойной арматурой |
при армировании сечения
одиночной арматурой только в растянутой зоне |
|||
|
Случай 1 |
Любая |
Sc<0,8S0 z£h0-a¢ |
Положение нейтральной оси определяется из уравнения
|
Положение нейтральной оси определяется из уравнения
|
|
Прямоугольная |
х<0,55h0 х³2a¢ |
Положение нейтральной оси определяется из уравнения |
Положение нейтральной оси определяется из уравнения |
|
|
Случай 2 |
Любая |
Sc³0,8S0 |
Положение нейтральной оси
определяется из уравнения (8) |
Положение нейтральной оси определяется из уравнения
(10) |
|
Прямоугольная |
х³0,55h0 |
Положение нейтральной оси определяется из уравнения
(12) |
Положение нейтральной оси определяется из уравнения
(14) |
|
Обозначения, принятые в табл.
2:
S0 - статический
момент всего сечения кладки относительно центра тяжести растянутой As или менее сжатой арматуры;
Sc -
статический момент сжатой зоны сечения кладки относительно центра тяжести
растянутой As или менее сжатой арматуры;
ScN - статический момент сжатой зоны кладки относительно точки приложения
силы;
z -
расстояние от центра тяжести сжатой зоны кладки до центра тяжести арматуры Аs;
S¢0 -
статический момент площади всего сечения относительно центра тяжести сечения
сжатой арматуры А¢s;
Ss и S¢s -
соответственно статические моменты площади сечения арматуры А¢s относительно центра тяжести
менее сжатой или растянутой арматуры Аs и арматуры Аs
относительно центра тяжести арматуры А¢s;
е и е¢ - соответственно расстояние от точки приложения силы N до центра
тяжести арматуры Аs и А¢s;
b -
ширина сечения;
х - высота сжатой зоны;
a и a¢ - толщина защитного слоя
арматуры Аs и А¢s;
h0=h-а - расчетные высоты
сечения;
и h¢0=h-а¢
h - полная высота сечения.
Примечание. В формулах (8) и (12) знак „плюс" принимается при приложении
продольной силы за пределами расстояния между центрами тяжести арматуры Аs и
А¢s и
знак „минус" - при приложении продольной силы между центрами тяжести
арматуры Аs и А¢s.
ПОСЛЕДОВАТЕЛЬНОСТЬ И ФОРМУЛЫ
ПОДБОРА СЕЧЕНИЯ АРМАТУРЫ ПО ЗАДАННЫМ e0, N,
A, R, Rs
|
Сечения с двойной арматурой |
Сечения с одиночной арматурой |
||
|
произвольной формы |
прямоугольные |
произвольной формы |
прямоугольные |
|
Высоте
сжатой зоны х определяется по формуле (21) x=h0 при е0£0,22h0+0,5a |
Из
формул (9) и (10)
определяем
|
По
формулам (13) и (14)
определяем х:
|
|
|
В
случае 1 определяем Аs и А¢s из формулы (7) и формулы
(8) (см. табл. 2) |
В
случае 1 определяем Аs и А¢s из формул (11) и (12)
(см. табл. 2) |
По
найденному |
Если
х<0,55h0, то As
определяем по формуле (33) |
|
Если
Sc<0,8S0, то количество арматуры Аs
определяем по формуле
|
|
||
|
Проверяем
условие z£h0-a¢ |
Проверяем
условие х³2a¢ |
Если
Sc³0,8S0, расчет ведется по случаю 2 (см.
табл. 2) внецентренного сжатия, и арматура Аs определяется по формуле
(23), а прочность сжатой зоны
проверяется по формуле (17) |
Если
х³0,55h0,
имеем случай 2 внецентренного сжатия, и арматура Аs определяется по формуле (33), в прочность сжатой
зоны проверяется по формуле (20) |
|
В
случае 2А¢s и Аs определяем из формул (15) и (16) (см. табл. 2)
|
В
случае 2А¢s
определяем из формул (18)
и (19) (см. табл. 2)
|
- |
- |
|
Арматура Аs определяется по формуле (23). При
расположении N между А¢s и Аs необходимо дополнительное соблюдение условия,
чтобы
|
а арматуру Аs определяем по формуле (27). При
расположении N между арматурами А¢s и Аs необходимо дополнительное соблюдение условия, чтобы
|
- |
- |
Примечания: 1. В формулах (22) и (26) знак «плюс» перед А¢s и е¢/е принимается при
расположении продольной силы N между центрами тяжести арматуры Аs и А¢s и знак «минус» - при
расположении продольной силы за пределами центра тяжести арматуры Аs и А¢s, в формулах (23) и (27) - наоборот.
2. Условные обозначения см. в
табл. 2.
3. Формула (21) определяет
значение х, соответствующее минимальному расходу арматуры.
ПОСЛЕДОВАТЕЛЬНОСТЬ РАСЧЕТА
ПРИ ОПРЕДЕЛЕНИИ РАСЧЕТНОЙ НЕСУЩЕЙ СПОСОБНОСТИ Nu ЭЛЕМЕНТА С ПРОДОЛЬНОЙ
АРМАТУРОЙ ПО ЗАДАННЫМ e0, A,
As, A¢s R И Rs (ПРИ ИСПОЛЬЗОВАНИИ ДЛЯ ВЫЧИСЛЕНИЯ ФОРМУЛ ТАБЛ. 2 ПРИНИМАЕТСЯ Nu=N)
|
Сечения с двойной
арматурой |
Сечения с одиночной
арматурой |
||
|
произвольной формы |
прямоугольные |
произвольной формы |
прямоугольные |
|
Определяем ScN из формулы
(8) |
Определяем х из формулы (12) |
Определяем ScN из формулы (10)
|
Определяем х из формулы (14)
|
|
По ScN определяем х и по х находим Sc,
которое сравниваем с S0 |
Если полученное значение х<0,55h0, то по формуле (11) определяем Nu=N
и дополнительно проверяем х³2a¢ |
По ScN определяем х, а по х
находим Sc и сравниваем Sc с S0 |
Если х<0,55h0, то по формуле (13) определяем Nu=N |
|
Если Sс<0,8S0, определяем x и по формуле (7) несущую способность сечения. Проверяется условие z£h0-а¢ |
Если х³0,55h0х, то Nu=N
определяем по формуле (18) |
Если Sc<0,8S0, то вычисляем Ac по формуле (9) и находим Nu=N |
Если х³0,55h0, то Nu=N определяется по формуле (20) |
|
Если Sс>0,8S0, то несущая
способность сечения определяется по формуле (15). В случаях, когда N располагается между
арматурами Аs и А¢s,
необходимо дополнительно проверить по формуле (16) За расчетное Nu
принимается меньшее значение N из формул
(15) и (16) |
При расположении N между арматурами Аs
и А¢s
необходимо N определить по дополнительному условию (19). За расчетное Nu
принимается меньшее значение N из формул (18) и (19) |
Если Sc>0,8S0, то Nu=N определяем по формуле
(17) |
- |
Примечание. В формулах (34) и (35) знак «минус»
принимается при приложении продольной силы за пределами расстояния между
центрами тяжести арматуры Аs и А¢s, знак «плюс» - при
приложении продольной силы между центрами тяжести арматуры Аs и
А¢s.
ПРИЛОЖЕНИЕ 8
РАСЧЕТ КАМЕННЫХ ЗДАНИЙ С ПРИМЕНЕНИЕМ ЭВМ
Расчет выполняется в последовательности:
1. Вычисление геометрических
характеристик горизонтальных сечений стен здания.
2. Определение ветровой
нагрузки на стены здания.
3. Определение перемещения
верха здания.
4. Вычисление вертикальных
нагрузок, постоянных и временных, действующих на стены здания.
5. Расчет стен.
6. Определение вертикальных
деформации кладки от длительно действующих на стены нагрузок и их сравнение.
7. Расчет поперечных стен на
главные растягивающие напряжения от горизонтальной (ветровой) нагрузки.
8. Расчет поперечных и
продольных стен в местах их взаимного примыкания на сдвиг от горизонтальной
(ветровой) нагрузки.
9. Вычисление нагрузок от
стен здания с учетом и без учета действия ветра.
1. ![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
где А - площадь
горизонтального сечения стены;
a
– номер вершины (черт. 1);
N - число вершин;
xa, ya - координаты вершин;
S, I -
статический момент и момент инерции относительно исходной оси oх (см. черт. 1);
ym - координата центра тяжести относительно центральной оси;
Im - момент инерции относительно оси, проходящей через центр тяжести
горизонтального сечения стены.
Ось оу располагается в
плоскости действия ветра и направляется в сторону наименее сжатого волокна.
Вершины многоугольника нумеруются по часовой стрелке (см. черт. 1).
Формулы приняты по Программе
расчета геометрических характеристик плоского сечения бруса произвольной
конфигурации, разработанной инж. Л. А. Павловой (СПКНБ, г. Одесса).
2. Ветровая распределенная
нагрузка на М-ю стену здания определяется по формуле (86).
Черт. 1. Нумерация вершин горизонтальных сечений стен здания
Интенсивность ветровой
нагрузки на здание и коэффициент, учитывающий изменение скоростного напора по
высоте, определяются в соответствии со СНиП 2.01.07-85:
для открытой местности типа А
(степи, лесостепи, пустыни, открытые побережья морей, озер, водохранилищ) по
формуле
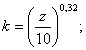 (6)
(6)
для местности типа В (города
с окраинами, лесные массивы и тому подобные местности, равномерно покрытые
препятствиями высотой более 10 метров) по формуле
 (7)
(7)
где z - расстояние от поверхности
земли до точки определения значения ветровой нагрузки;
при z < 10 м
![]()
![]()
Нормативное значение
динамической составляющей ветровой нагрузки принято по СНиП 2.01.07-85
Коэффициент m для
верха здания принимается:
для местности типа А по
формуле
![]() (8)
(8)
для местности типа В по
формуле
 (9)
(9)
Период собственных колебании
здания Т (в секундах) определяется по формуле
где h - высота здания;
n - вес
здания, отнесенный к 1 м его высоты;
Е - модуль деформации кладки,
определяется по формуле [8];
I - сумма
моментов инерции стен здания;
g -
ускорение силы тяжести.
Поперечная сила и изгибающий
момент от ветровой нагрузки определяются в уровне перекрытия каждого этажа (черт. 2) по формулам:
![]() (11)
(11)
где qv - интенсивность ветровой
нагрузки в уровне перекрытия;
Н - высота этажа;
Qw - поперечная сила в уровне перекрытия;
Mw - изгибающий момент в уровне перекрытия.
Черт. 2.
Обозначения поперечных сил и изгибающих моментов
в уровне перекрытия каждого этажа
3. Перемещение верха здания
определяется по формуле
 (13)
(13)
где q1 -
интенсивность ветровой нагрузки у поверхности земли;
q2 - интенсивность ветровой
нагрузки в уровне верха здания;
h - см. формулу (10)
приложения;
L -
фасадный размер здания;
Е - см. формулу (10)
приложения;
Ii - момент инерции горизонтальных сечений стен.
4. Нагрузки, действующие на
стены от перекрытий, определяются на 1 м2 в вертикальном сечении по
перекрытиям на всю высоту здания с нарастанием по высоте сверху вниз (черт. 3) по формуле
![]() (14)
(14)
где q - вес 1 м2 всех
перекрытий, сверху вниз, на уровне a-го перекрытия;
v - вес 1
м2 перекрытия, временная нагрузка;
g - вес 1
м2 перекрытия, постоянная нагрузка;
N - число
перекрытий.
Черт. 3. Определение вертикальных нагрузок по перекрытиям на всю высоту здания
Если временную нагрузку
необходимо принимать с понижением по высоте, то коэффициент понижения
принимается в соответствии со СНиП 2.01.07-85.
Нагрузки от собственного веса
стен на 1 м (черт. 4) определяются
по формуле
![]() (15)
(15)
G=gHbn, (16)
где qg - вес 1 м всей стены до
уровня a-го перекрытия сверху вниз;
G - вес 1 м стены этажа
здания;
N - число этажей;
Н - высота этажа с вычетом
проемов;
b -
толщина стены на этаже здания;
n -
коэффициент перегрузки стен здания;
g
- объемная масса кладки стен здания.
Нагрузки по вертикальным
сечениям стен от вертикальных нагрузок (см. черт. 4) поэтажно на 1 м стены определяются по формуле
где l - грузовой размер площади,
примыкающей к сечению в уровне a-го этажа;
М - количество нагрузок q, воздействующих
на одно сечение в уровне a-го этажа. М не должно быть
более трех.
Черт. 4. Определение вертикальных нагрузок от собственного веса стены
Нормальная сила от действия
вертикальных нагрузок для каждой стены поэтажно определяется по формуле
где N - число сечений,
представленных в данной стене;
LN - длина участка соответствующего сечения.
Пример. Нормальная сила для стены (черт. 5) на уровне a-го
этажа будет иметь вид
![]() при N=4.
при N=4.
Изгибающий момент от
вертикальных нагрузок, действующих на стену, относительно принятой оси 0х (см. черт. 5) определяется по формуле
![]() , (19)
, (19)
где еN -
расстояние от центра тяжести участка до оси 0х.
Черт. 5.
Определение изгибающего момента от
вертикальных нагрузок относительно оси 0х
Эксцентриситет приложения силы N относительно оси ох (черт. 6)
![]() (20)
(20)
Изгибающий момент от
вертикальных нагрузок относительно центра тяжести стены (см. черт. 6)
Mm=Nem, (21)
где em - расстояние от центра
тяжести стены до N.
5. Напряжения от сил N
определяются по формулам [13] и [29].
Расчетные сопротивления
армированной кладки Rskb - по формулам [31] и [32].
Напряжения от совместного
действия ветровой и нормальной нагрузок N определяются по формулам [13] и [29]
при эксцентриситете приложения силы N
![]() (22)
(22)
где Mm- следует принимать по формуле (21);
Mw - момент от ветровой нагрузки - по формуле (12);
N - по формуле (18).
Черт. 6.
Определение эксцентриситета точки приложения
силы N относительно оси 0х
Напряжения от действия ветра
на горизонтальные сечения стен в уровне a-го этажа определяются по
формуле
Rw=Ra-RN, (23)
где Ra - принимается по формулам
[13] и [29] от совместного действия ветровой и нормальной нагрузок;
RN - то же, только от действия нормальной нагрузки (черт. 7).
Расчетное сопротивление
кладки сжатию для каждой стены поэтажно определяется из условия
Ra<R, (24)
где R - принимается по табл. [2].
В исходных данных задаются
минимально допустимые конструктивно марки материалов (кирпич, раствор) для
верхних этажей здания. Для нижних этажей - максимально допустимые, определяемые
возможностями местной строительной базы.
Если условие (24) не выполняется,
то кладка армируется сетчатой арматурой в соответствии с формулой
Ra£Rskb,a£2R, (25)
Rskb,a - определяется по формулам
[31] и [32].
Процент сетчатого армирования
определяется по формуле
![]() (26)
(26)
где d - диаметр арматурной
проволоки;
с - размер ячейки сетчатой
арматуры в соответствии с п. [6.77];
hk - толщина кирпича:
N - число рядов кладки в
соответствии с пунктом [6.76].
Черт. 7. Определение напряжений от действия ветровой и нормальной нагрузок на горизонтальные сечения стен в уровне a-го этажа
Толщина шва в кирпичной
кладке принята равной 12 мм.
6. Для определения
вертикальных деформаций кладки вычисляются по вертикальным сечениям стен (см. черт. 4) длительно действующие
нагрузки поэтажно на 1 м стены по формуле (18).
Деформации сжатия кладки
определяются с коэффициентом 2/3, что означает учет работы перекрытий в
качестве шпонок при условии заведения продольных ребер плит в кладку стен на
расстояние не менее 100 мм.
Напряжения в кладке от
длительно действующей нагрузки определяются по формуле
![]() , (27)
, (27)
где qtot,N -
определяется по формуле (17);
b -
толщина стены.
Разности деформаций двух
смежных стен определяются по формуле
(91).
Предельную (допустимую)
разность деформаций стен следует принимать по табл. 13.
7. Расчет стен на главные
растягивающие напряжения производится по формулам [40] - [44].
8. Расчет стен в местах их
взаимного примыкания производится по формуле [38].
9. Нагрузки от стен на 1 м с
учетом действия ветра определяются по формуле
qtot=qtot,N+Rwb, (28)
где qtot,N -
по формуле (17);
Rw - напряжения от действия ветра определятся по формуле (23);
b -
толщина стены (см. черт. 4).
Расход арматуры, кг, на 1 м3
кладки, определяется по формуле
m=78,5m, (29)
где m
- процент армирования.
Пример. Выполнить статический расчет
на ЭВМ 14-этажного жилого дома. Длина здания с учетом лоджии 37,51 м, высота -
46,00 м. План и разрез здания приведены на черт. 8 и 9,
горизонтальные сечения всех стен (элементов) - на черт. 10.
Условия строительства:
Москва. Толщина наружных стен 510мм; толщина части внутренних стен принята
переменной по высоте здания: 1-4 этажи - 510 мм, 5-12 - 380 мм, 13-15 - 250 мм.
Наружные стены выполняются из керамических камней 250´138´120 мм плотностью g=1600
кг/м3, внутренние - из обыкновенного глиняного кирпича. Перекрытия -
сборные железобетонные, замоноличенные.
Расчет выполнен по KИРП-1 -
Программа по расчету кирпичных зданий повышенной этажности - на ЕС ЭВМ,
разработанной ЦНИИСК им. Кучеренко совместно с институтом Башкиргражданпроект.
КИРП-1 написана на языке ФОРТРАН-IV*. Сбор вертикальных нагрузок
осуществляется автоматически. При расчете на горизонтальную нагрузку в качестве
расчетной схемы здания принят набор консольных стержней, имеющих произвольное
поперечное сечение. В зависимости от жесткости элементов определяется доля
расчетной горизонтальной (ветровой) нагрузки, приводящейся на них. При этом
учитываются динамическая составляющая ветра и коэффициент динамичности в
зависимости от периода собственных колебаний здания в соответствии со СНиП 2.01.07-85.
* В программировании на языке ФОРТРАН
принимала участие инженер-программист института Башкиргражданпроект Т.Ф.
Герасимова.
Вся
информация как исходная, так и полученная в результате расчета, выдается на ЭВМ
в виде таблиц, позволяющих оценить напряженно-деформированное состояние
кирпичных стен. Перед началом расчета стены разбиваются на расчетные элементы,
которые в дальнейшем именуются «стены». Иллюстрация исходных данных, а также
результатов расчета приводится на примере стен 1, 2, 7,8,10, 15, 20, 25 (см.
план здания, черт. 8) при действии
ветра со стороны главного фасада. Расчет стен со стороны торцевого фасада
аналогичен расчету стен со стороны главного фасада. При конструировании
принимается наибольшие усилия, полученные из указанных расчетов.
Черт. 8. План здания
Черт. 9. Разрез здания
Черт. 10. Горизонтальные сечения всех стен здания (элементов)
Данные о ветровой нагрузке,
кирпичной кладке, возможном сетчатом армировании, параметрах здания (этажность,
наличие подвала и др.) приводятся в первых шести таблицах исходных данных.
Геометрические размеры стен задаются в координатной системе (черт. 11, табл. 1).
Сбор вертикальных нагрузок
выполняется в следующей последовательности. Сначала формируется таблица
нагрузок (табл. 2), в которой
указываются нагрузки от перекрытий различного назначения: кровли, чердака,
квартиры, коридора, лоджии, лестницы - с выделением кратковременной, постоянной
и длительной частей нагрузок. Таким образом, имеем всего семь типов нагрузок.
Далее заполняется таблица нагрузок с площади (табл. 3) в соответствии с черт. 3 и 4.
Расчетные нагрузки от собственного веса стен с учетом штукатурки приведены в табл. 4.
Черт. 11. Геометрические размеры горизонтальных сечений рассматриваемых элементов
ГЕОМЕТРИЧЕСКИЕ РАЗМЕРЫ СТЕН В
КООРДИНАТНОЙ СИСТЕМЕ
|
Номер стены/Число
координат |
Номер точки |
Привязка по оси х, м |
Привязка по оси y, м |
|
1/10 |
1 |
1,33 |
0 |
|
2 |
1,33 |
2,64 |
|
|
3 |
0 |
2,64 |
|
|
4 |
0 |
3,15 |
|
|
5 |
1,33 |
3,15 |
|
|
6 |
1,33 |
3,20 |
|
|
7 |
1,84 |
3,20 |
|
|
8 |
1,84 |
0,51 |
|
|
9 |
3,40 |
0,51 |
|
|
10 |
3,40 |
0 |
НАГРУЗКИ
|
№ п.п |
Назначение |
Полные расчетные нагрузки,
кН/м2 |
Длительно действующие
расчетные нагрузки, кН/м2 |
||
|
кратковременные |
постоянные |
длительная часть |
постоянные |
||
|
1 |
Кровля |
1,40 |
5,00 |
0,42 |
5,00 |
|
2 |
Чердак |
0,91 |
3,90 |
0 |
3,90 |
|
3 |
Квартира |
1,95 |
5,00 |
0,39 |
5,00 |
|
4 |
Коридор |
3,60 |
3,90 |
1,30 |
3,90 |
|
5 |
Лоджия |
1,95 |
3,90 |
0,39 |
3,90 |
|
6 |
Лестница |
3,60 |
3,00 |
1,30 |
3,00 |
|
7 |
Подвал |
0 |
0 |
0 |
0 |
СБОР НАГРУЗОК С ПЛОЩАДИ
|
№ п. п. |
Этаж |
Тип нагрузки (по табл. 2) |
Учет снижения по высоте: 1
– «да» 0 – «нет» |
|
|
1 |
Кровля |
1 |
0 |
|
|
Чердак |
2 |
0 |
||
|
14-1 |
3 |
1 |
||
|
Подвал |
7 |
0 |
||
|
2 |
Кровля |
1 |
0 |
|
|
Чердак |
2 |
0 |
||
|
14-1 |
4 |
0 |
||
|
Подвал |
7 |
0 |
||
|
3 |
Кровля |
1 |
0 |
|
|
Чердак |
2 |
0 |
||
|
14-1 |
5 |
1 |
||
|
Подвал |
7 |
0 |
||
|
4 |
Кровля |
1 |
0 |
|
|
Чердак |
2 |
0 |
||
|
14-1 |
6 |
0 |
||
|
Подвал |
7 |
0 |
||
|
5 |
Кровля |
1 |
0 |
|
|
Чердак |
2 |
0 |
||
РАСЧЕТНЫЕ НАГРУЗКИ ОТ
СОБСТВЕННОГО ВЕСА СТЕН
|
№ п. п. |
Этаж |
Толщина стены, м |
Высота стены, м |
Признак стены (1 -
наружная, 0 - внутренняя) |
|
1 |
Чердак |
0,38 |
2,40 |
1 |
|
14-1 |
0,53 |
3,00 |
||
|
Подвал |
0,50 |
2,20 |
||
|
2 |
Чердак |
0,38 |
2,40 |
1 |
|
14-1 |
0,53 |
1,20 |
||
|
Подвал |
0,50 |
2,20 |
||
|
3 |
Чердак |
0,25 |
2,00 |
0 |
|
14-13 |
0,29 |
3,00 |
||
|
12-5 |
0,42 |
3,00 |
||
|
4-1 |
0,55 |
3,00 |
||
|
Подвал |
0,50 |
2,20 |
||
|
4 |
Чердак |
0,38 |
2,00 |
0 |
|
14-5 |
0,42 |
3,00 |
||
|
4-1 |
0,55 |
3,00 |
||
|
Подвал |
0,50 |
2,20 |
||
|
5 |
Чердак |
0,25 |
0,40 |
0 |
|
14-13 |
0,29 |
0,90 |
||
|
12-5 |
0,42 |
0,90 |
||
|
4-1 |
0,55 |
0,90 |
||
|
Подвал |
0,50 |
0,50 |
Формирование сечений
приводится в табл.5. Номер нагрузки с
площади принимается по табл. 3,
номер стены - по табл. 4, грузовые
paзмеры - в соответствии с черт.
4 и 8. Формирование сечений
приведено для части стен, рассматриваемых в примере. Сбор нагрузок на стены
приведен в табл. 6 в соответствии
с черт. 5 и 11 на примере стены № 1. Распределение
«фронтального размера» (длина здания с учетом лоджий) принимается в
соответствии с формулой (86) п. 7.8, данные для сравнения деформаций
приводятся в соответствующих таблицах. Исходные данные для обратной задачи
приведены в табл.7.
ФОРМИРОВАНИЕ СЕЧЕНИЙ
|
Номер сечения |
Пролет - 1 |
Пролет - 2 |
Номер стены (по табл.1) |
||
|
Грузовой размер, м |
Номер нагрузки с площади
(по табл. 2) |
Грузовой размер, м |
Номер нагрузки с площади
(по табл. 3) |
||
|
1-1 |
3,01 |
1 |
- |
- |
1 |
|
2-2 |
- |
- |
- |
- |
1 |
|
3-3 |
2,97 |
3 |
- |
- |
1 |
|
4-4 |
3,01 |
1 |
- |
- |
2 |
|
6-6 |
5,94 |
3 |
- |
- |
1 |
|
9-9 |
2,74 |
1 |
- |
- |
1 |
|
10-10 |
2,74 |
1 |
- |
- |
2 |
|
28-28 |
0,71 |
2 |
0,50 |
1 |
3 |
|
30-30 |
0,71 |
2 |
0,50 |
1 |
5 |
|
31-31 |
6,07 |
1 |
- |
- |
4 |
|
46-46 |
- |
- |
- |
- |
12 |
|
47-47 |
- |
- |
- |
- |
13 |
|
50-50 |
0,25 |
1 |
- |
- |
l |
|
51-51 |
0,50 |
1 |
- |
- |
1 |
|
52-52 |
0,50 |
1 |
- |
- |
2 |
|
61-61 |
0,71 |
2 |
- |
- |
3 |
|
62-62 |
0,71 |
2 |
0,25 |
1 |
3 |
|
63-63 |
0,50 |
1 |
- |
- |
4 |
СБОР НАГРУЗОК НА СТЕНЫ
|
Номер стены/Число
координат |
Номер сечения |
Размер грузового участка
стены, м |
Привязка грузового участка
к оси х, м |
|
1/10 |
1-1 |
2,19 |
2,105 |
|
2-2 |
0,51 |
0,255 |
|
|
3-3 |
1,33 |
2,895 |
|
|
4-4 |
1,04 |
3,20 |
|
|
46-46 |
3,48 |
3,15 |
|
|
47-47 |
2,97 |
3,15 |
|
|
50-50 |
0,50 |
0,76 |
|
|
50-50 |
0,50 |
0,255 |
|
|
51-51 |
1,06 |
0,255 |
|
|
52-52 |
0,68 |
0,255 |
ДАННЫЕ ДЛЯ ОБРАТНОЙ ЗАДАЧИ
|
Этаж |
Расчетные сопротивления
сжатию кирпичной кладки, МПа |
Марка |
|
|
кирпича |
раствора |
||
|
1-4 |
2,2 |
150 |
100 |
|
5-6 |
2,0 |
125 |
100 |
|
7-8 |
1,7 |
100 |
75 |
|
9-10 |
1,3 |
75 |
50 |
|
11-15 |
0,9 |
50 |
25 |
Результаты расчета выдаются в
табличной форме. Кроме того, на печать выдаются общие данные для всего здания:
период колебаний здания, с ........ 2,286
коэффициент динамичности ........ 1,522
высота здания, м ........... 46,00
вес здания, кН ............. 117042,44
вес 1 м знания, кН ........... 2544,40
суммарный момент инерции стен
(элемента) здания, м4 .294,984
прогиб верха здания, м ........... 0,018
относительная величина
прогиба ........ 1/2552
расход стали на сетчатое
армирование, кг ..... l39,94
Taбл. 8 дает возможность проанализировать нагрузки от
ветра, вертикальные нагрузки и долю ветра в процентах от вертикальной нагрузки
на стены здания поэтажно.
В табл. 9 приведены напряжения в стенах поэтажно и по
возрастающей, что дает возможность принять решение для обратной задачи, т. е.
на каком этаже менять марки материалов и горизонтальное поперечное сечение
внутренних стен по высоте здания. В табл.
10 приводятся марки материалов (кирпича, раствора), необходимость сетчатого
армирования, процент использования несущей способности стен поэтажно. В табл. 11 приводятся результаты
расчета на главные растягивающие напряжения с указанием на необходимость
армирования горизонтальных швов кладки стен, использование несущей способности
стен в процентах поэтажно. В табл.
12 приводятся результаты расчета на восприятие сдвигающих усилий от ветра в
местах примыкания стен с указанием использования несущей способности в
процентах поэтажно. В табл. 13
приведены результаты расчета сравнения деформаций по пяти этажам, начиная с
первого до пятого, со второго по шестой и т. д. с приведением разности
деформаций по всей высоте стен здания.
РЕЗУЛЬТАТЫ РАСЧЕТА ДЛЯ 1-ГО
ЭТАЖА
|
Номер стены |
Нагрузки, кН, кН×м |
Доля ветра Rw от RN, % |
|||
|
горизонтальные (ветровые) |
вертикальные |
||||
|
Q |
Mw |
N |
MN |
||
|
1 |
17,3 |
420,3 |
4085,8 |
1290,2 |
4,7 |
|
2 |
0,4 |
9,6 |
1630,8 |
101,0 |
1,4 |
|
7 |
87,4 |
2119,5 |
6887,1 |
126,9 |
7,2 |
|
8 |
341,4 |
8280,9 |
12599,1 |
2734,4 |
14,5 |
|
10 |
0,1 |
1,5 |
1556,2 |
0 |
0,1 |
|
15 |
188,2 |
4565,1 |
10317,5 |
3367,3 |
8,1 |
|
17 |
202,4 |
4910,0 |
10192,7 |
2168,2 |
9,5 |
|
20 |
2,8 |
67,9 |
7535,2 |
332,4 |
1,0 |
|
25 |
70,9 |
1718,9 |
3988,5 |
934,0 |
17,7 |
ПОЭТАЖНЫЕ НАПРЯЖЕНИЯ RN+Rw
|
Номер стены |
Этаж |
||||||||||||||
|
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
|
2 |
0,14 |
0,30 |
0,50 |
0,69 |
0,88 |
1,06 |
1,25 |
1,43 |
1,61 |
1,79 |
1,97 |
2,15 |
2,35 |
2,53 |
2,71 |
|
16 |
0,13 |
0,30 |
0,50 |
0,69 |
0,88 |
1,07 |
1,25 |
1,43 |
1,62 |
1,80 |
1,98 |
2,16 |
2,34 |
2,52 |
2,71 |
|
10 |
0,12 |
0,28 |
0,45 |
0,63 |
0,80 |
0,97 |
1,13 |
1,30 |
1,47 |
1,63 |
1,80 |
1,96 |
2,13 |
2,29 |
2,45 |
|
21 |
0,11 |
0,24 |
0,40 |
0,55 |
0,70 |
0,85 |
1,00 |
1,15 |
1,29 |
1,44 |
1,58 |
1,73 |
1,87 |
2,03 |
2,17 |
|
19 |
0,07 |
0,19 |
0,31 |
0,44 |
0,57 |
0,69 |
0,82 |
0,94 |
1,07 |
1,19 |
1,32 |
1,44 |
1,56 |
1,69 |
1,81 |
|
9 |
0,09 |
0,20 |
0,33 |
0,46 |
0,58 |
0,70 |
0,82 |
0,94 |
1,06 |
1,18 |
1,30 |
1,42 |
1,54 |
1,66 |
1,78 |
|
25 |
0,08 |
0,17 |
0,28 |
0,39 |
0,50 |
0,62 |
0,73 |
0,85 |
0,97 |
1,09 |
1,23 |
1,34 |
1,47 |
1,60 |
1,73 |
|
17 |
0,13 |
0,27 |
0,44 |
0,46 |
0,59 |
0,73 |
0,86 |
0,99 |
1,12 |
1,26 |
1,39 |
1,29 |
1,42 |
1,54 |
1,67 |
|
14 |
0,09 |
0,19 |
0,31 |
0,42 |
0,54 |
0,65 |
0,76 |
0,88 |
0,99 |
1,10 |
1,21 |
1,32 |
1,43 |
1,55 |
1,66 |
|
15 |
0,11 |
0,22 |
0,36 |
0,47 |
0,60 |
0,73 |
0,85 |
0,99 |
1,11 |
1,25 |
1,37 |
1,28 |
1,41 |
1,53 |
1,65 |
|
1 |
0,08 |
0,18 |
0,28 |
0,39 |
0,50 |
0,61 |
0,71 |
0,82 |
0,92 |
1,03 |
1,13 |
1,24 |
1,35 |
1,46 |
1,56 |
|
4 |
0,06 |
0,16 |
0,27 |
0,38 |
0,48 |
0,59 |
0,69 |
0,80 |
0,91 |
1,01 |
1,12 |
1,22 |
1,33 |
1,43 |
1,54 |
|
3 |
0,08 |
0,17 |
0,27 |
0,46 |
0,59 |
0,71 |
0,83 |
0,96 |
1,08 |
1,20 |
1,32 |
1,18 |
1,29 |
1,40 |
1,51 |
|
22 |
0,06 |
0,16 |
0,26 |
0,36 |
0,46 |
0,57 |
0,67 |
0,77 |
0,87 |
0,97 |
1,07 |
1,17 |
1,27 |
1,38 |
1,48 |
|
23 |
0,06 |
0,16 |
0,26 |
0,36 |
0,46 |
0,57 |
0,67 |
0,77 |
0,87 |
0,97 |
1,07 |
1,17 |
1,27 |
1,38 |
1,48 |
|
24 |
0,06 |
0,16 |
0,26 |
0,36 |
0,46 |
0,57 |
0,67 |
0,77 |
0,87 |
0,97 |
1,07 |
1,17 |
1,27 |
,38 |
1,48 |
|
5 |
0,07 |
0,17 |
0,27 |
0,38 |
0,48 |
0,58 |
0,68 |
0,78 |
0,88 |
0,98 |
1,08 |
1,18 |
1,28 |
1,38 |
1,48 |
|
11 |
0,11 |
0,22 |
0,36 |
0,40 |
0,51 |
0,63 |
0,75 |
0,86 |
0,99 |
1,11 |
1,22 |
1,13 |
1,24 |
1,36 |
1,47 |
|
20 |
0,07 |
0,15 |
0,24 |
0,41 |
0,52 |
0,64 |
0,75 |
0,87 |
0,98 |
1,10 |
1,21 |
1,14 |
1,24 |
1,35 |
1,46 |
|
18 |
0,07 |
0,17 |
0,27 |
0,37 |
0,47 |
0,57 |
0,67 |
0,76 |
0,86 |
0,96 |
1,06 |
1,15 |
1,25 |
1,35 |
1,44 |
|
7 |
0,13 |
0,28 |
0,45 |
0,43 |
0,55 |
0,67 |
0,79 |
0,90 |
1,03 |
1,14 |
1,27 |
1,11 |
1,22 |
1,33 |
1,44 |
|
13 |
0,09 |
0,19 |
0,31 |
0,37 |
0,48 |
0,61 |
0,72 |
0,83 |
0,94 |
1,05 |
1,16 |
1,09 |
1,19 |
1,30 |
1,40 |
|
6 |
0,05 |
0,14 |
0,24 |
0,33 |
0,43 |
0,52 |
0,62 |
0,71 |
0,80 |
0,90 |
0,99 |
1,08 |
1,17 |
1,27 |
1,36 |
|
12 |
0,06 |
0,14 |
0,23 |
0,31 |
0,40 |
0,49 |
0,57 |
0,66 |
0,75 |
0,84 |
0,93 |
1,03 |
1,12 |
1,21 |
1,31 |
|
8 |
0,07 |
0,16 |
0,26 |
0,31 |
0,41 |
0,50 |
0,59 |
0,71 |
0,80 |
0,90 |
1,00 |
0,94 |
1,04 |
1,14 |
1,26 |
МАРКИ МАТЕРИАЛОВ
|
Номер стены |
Напряжение, МПа |
Армирование |
Марка |
Использование несущей
способности стены, % |
|||||||
|
RN+Rw |
R или Rskb |
% |
Диаметр, мм |
Размер ячейки, мм |
Через число рядов |
Объем кладки, м3 |
Расход стали, кг |
кирпича |
раствора |
||
|
1 |
1,56 |
2,20 |
- |
- |
- |
- |
9,3 |
- |
150 |
100 |
70,9 |
|
2 |
2,71 |
2,77 |
0,157 |
3 |
30 |
2 |
2,0 |
24,3 |
150 |
100 |
97,8 |
|
7 |
1,44 |
2,20 |
- |
- |
- |
- |
15,3 |
- |
150 |
100 |
65,6 |
|
8 |
1,26 |
2,20 |
- |
- |
- |
- |
34,9 |
- |
150 |
100 |
57,4 |
|
10 |
2,45 |
2,68 |
0,105 |
3 |
30 |
3 |
2,0 |
16,2 |
150 |
100 |
91,5 |
|
15 |
1,65 |
2,20 |
- |
- |
- |
- |
21,3 |
- |
150 |
100 |
74,9 |
|
17 |
1,67 |
2,20 |
- |
- |
- |
- |
20,5 |
- |
150 |
100 |
75,9 |
|
20 |
1,46 |
2,20 |
- |
- |
- |
- |
16,1 |
- |
150 |
100 |
66,2 |
|
25 |
1,73 |
2,20 |
- |
- |
- |
- |
8,7 |
- |
150 |
100 |
78,4 |
РЕЗУЛЬТАТЫ РАСЧЕТА
НА ГЛАВНЫЕ РАСТЯГИВАЮЩИЕ НАПРЯЖЕНИЯ
|
Номер стены |
Напряжение, МПа |
Использование несущей
способности стены, % |
|
|
Rq |
Rtq или Rstq |
||
|
1 |
0,0077 |
0,4451 |
1,7 |
|
2 |
0,0010 |
0,5587 |
0,2 |
|
7 |
0,0227 |
0,4201 |
5,4 |
|
8 |
0,0560 |
0,3993 |
14,0 |
|
10 |
0,00014 |
0,5195 |
0,03 |
|
15 |
0,0422 |
9,4528 |
9,3 |
|
17 |
0,0459 |
0,4528 |
10,1 |
|
20 |
0,0012 |
0,4171 |
0,3 |
|
25 |
0,0507 |
0,4641 |
10,9 |
РЕЗУЛЬТАТЫ РАСЧЕТА
НА ВОСПРИЯТИЕ СДВИГАЮЩИХ УСИЛИЙ ОТ ВЕТРА
|
Номер стены |
Поперечная сила от ветра
Q, кН |
Напряжение, МПа |
Координаты примыкания стен,
м |
Использование несущей
способности, % |
|
|
Rsq/4 |
фактическое |
||||
|
1 |
17,33 |
0,20 |
0,0003 |
3,15 |
0,2 |
|
|
0,0111 |
2,64 |
5,6 |
||
|
|
0,0115 |
0,51 |
5,8 |
||
|
15 |
188,21 |
0,20 |
0,0180 |
7,60 |
9,2 |
|
|
0,0370 |
7,09 |
18,7 |
||
|
|
0,0420 |
0,51 |
20,9 |
||
РЕЗУЛЬТАТЫ РАСЧЕТА СРАВНЕНИЯ
ДЕФОРМАЦИЙ ПО ПЯТИ ЭТАЖАМ
|
Стены |
1 |
7 |
8 |
15 |
17 |
20 |
25 |
|||||||
|
Сравниваемые сечения |
1-3 |
1-50 |
53-67 |
55-66 |
2-15 |
21-22 |
31-63 |
2-6 |
32-68 |
50-68 |
33-50 |
2-33 |
2-3 |
3-50 |
|
Сравнение деформаций по пяти этажам, максимальные
значения, мм |
0,4 |
1,9 |
2,2 |
1,5 |
1,3 |
0,7 |
4,1 |
3,4 |
4,1 |
0,1 |
1,4 |
1,6 |
1,7 |
1,5 |
|
Сравнение деформаций на всю высоту здания, мм |
0,9 |
4,8 |
6,3 |
4,5 |
3,3 |
2,0 |
11,7 |
8,8 |
12,2 |
0,6 |
3,6 |
4,1 |
4,4 |
4,0 |
Из анализа результатов
расчета, приведенных в табл. 13,
следует, что доля ветра от вертикальной нагрузки для стен первого этажа
меняется от 0,1 (стена № 10) до 17,7% (стена № 25). Для диафрагм эта величина
изменяется в пределах 7,2% (стена № 7) и до 17,7% (стена № 25).
Из табл. 9 следует, что все простенки (стены), на которые
опираются перекрытия полным пролетом, являются наиболее нагруженными (см. стены
№ 2, 10, 16, 21). В остальных стенах напряжения изменяются на первом этаже от
1,81 (стена № 19) до 1,26 МПа (стена № 8), в том числе в диафрагмах (№7, 8, 11,
12, 15, 17, 25) от 1,26 до 1,73 МПа. Принимаем процент использования несущей
способности кладки для рабочих чертежей равным 100%. Простенки на первых трех
этажах следует армировать.
В табл. 10 приведены данные расчета
стен при назначенных марках материала для первого этажа здания. Из результатов
расчета следует, что простенки 2, 10, 16 армируются сетчатой арматурой из стали
Вр-1 Æ3 с ячейкой 30´30 мм через 2, 3, 2 ряда, т. е. сетки
укладываются на расстоянии 300, 450, 300 мм друг от друга по высоте. В этой
таблице для армируемых стен приводится расход стали на сетчатое армирование, 1
кг на стену (элемент) поэтажно, что дает возможность оценить расход стали в
натуральном выражении. Процент использования несущей способности стен
изменяется в пределах 97,8% для простенка (стены) № 2, до 57,4% для стены № 8.
Результаты расчета (см. табл. 11) показывают, что
использование несущей способности кладки на главные растягивающие напряжения
находится в пределах 0,03-14,0%.
Фактическое напряжение в
стене для сравнения с Rtq и Rstq определялось по формуле
![]()
остальные обозначения те же,
что и в п. [6.12].
Использование несущей
способности стен на восприятие сдвигающих усилий (см. табл. 12) для приведенных в таблице стен не превышает 21%.
Максимальные
разности деформаций для всех стен, сравниваемых по пяти этажам, находятся в
пределах 0,1 мм для сечения 50-68 (стена № 17) - 4,1 мм для сечения 31-63
(стена № 15) и 32-68 (стена № 17), что не превышает нормируемой величины 7 мм.
Разности деформаций на всю высоту здания находятся в пределах 0,6 мм для
сечения 50-68 (стена № 17) - 12,2 мм для сечения 32-68 (стена № 17), что не
превышает нормируемой величины 15 мм.
ПРИЛОЖЕНИЕ 9
ТАБЛИЦЫ ВЕЛИЧИН, ПРИМЕНЯЕМЫХ
ПРИ РАСЧЕТЕ ТОНКОСТЕННЫХ СВОДОВ ДВОЯКОЙ КРИВИЗНЫ
КООРДИНАТЫ x
И у И ТАНГЕНСЫ tgj УГЛОВ,
ОБРАЗУЕМЫХ КАСАТЕЛЬНЫМИ С ГОРИЗОНТАЛЬЮ,
ДЛЯ РАЗЛИЧНЫХ ТОЧЕК ОСИ СВОДА ПРИ ОЧЕРТАНИИ
ЕЕ ПО ЦЕПНОЙ ЛИНИИ, ПО ОКРУЖНОСТИ И ПО КВАДРАТНОЙ ПАРАБОЛЕ
|
f/l |
Значения у и tgj при х/l,
равном |
Множитель |
||||||||||||||||||||
|
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
0,5 |
||||||||||||
|
По цепной линии |
|
|||||||||||||||||||||
|
1/2 |
у=0,00 tgj=2,44 |
0,22 2,04 |
0,40 1,70 |
0,55 1,40 |
0,68 1,14 |
0,79 0,90 |
0,87 0,70 |
0,93 0,51 |
0,97 0,33 |
0,99 0,16 |
1,00 0,00 |
f - |
||||||||||
|
1/3 |
у=0,00 tgj=1,49 |
0,21 1,29 |
0,39 1,10 |
0,54 0,93 |
0,67 0,78 |
0,77 0,63 |
0,85 0,49 |
0,92 0,36 |
0,96 0,24 |
0,99 0,12 |
1,00 0,00 |
f - |
||||||||||
|
1/4 |
у=0,00 tgj=1,07 |
0,20 0,94 |
0,38 0,82 |
0,53 0,70 |
0,66 0,59 |
0,76 0,48 |
0,85 0,38 |
0,92 0,28 |
0,96 0,19 |
0,99 0,09 |
1,00 0,00 |
f - |
||||||||||
|
1/5 |
у=0,00 tgj=0,85 |
0,20 0,75 |
0,37 0,65 |
0,52 0,56 |
0,65 0,48 |
0,76 0,39 |
0,85 0,31 |
0,91 0,23 |
0,96 0,15 |
0,99 0,08 |
1,00 0,00 |
f - |
||||||||||
|
По окружности |
||||||||||||||||||||||
|
1/6 |
у=0,00 tgj=0,75 |
0,209 0,641 |
0,386 0,547 |
0,538 0,464 |
0,665 0,386 |
0,770 0,315 |
0,854 0,247 |
0,918 0,183 |
0,964 0,121 |
0,991 0,061 |
1,00 0,00 |
f - |
||||||||||
|
По окружности |
||||||||||||||||||||||
|
1/7 |
у=0,00 tgj=0,621 |
0,202 0,540 |
0,379 0,467 |
0,530 0,399 |
0,658 0,335 |
0,765 0,274 |
0,850 0,216 |
0,917 0,16 |
0,963 0,107 |
0,991 0,053 |
1,00 0,00 |
f - |
||||||||||
|
По квадратной параболе |
||||||||||||||||||||||
|
- |
у=0,00 tgj=4,00 |
0,19 3,60 |
0,36 3,20 |
0,51 2,80 |
0,64 2,40 |
0,75 2,00 |
0,84 1,60 |
0,91 1,20 |
0,96 0,80 |
0,99 0,40 |
1,00 0,00 |
f f/l |
||||||||||
ОПОРНЫЕ РЕАКЦИИ В
ДВУХШАРНИРНОЙ АРКЕ
ПАРАБОЛИЧЕСКОГО ОЧЕРТАНИЯ
|
Схемы загружения |
||
|
|
|
|
|
Вертикальные реакции |
||
|
VA=VB=0,5gl; |
VA=VB=0,167g1l |
VA=0,375pl; VB=0,125pl |
|
Распор |
||
|
|
|
|
При наличии затяжек
коэффициент k учитывает влияние упругого удлинения затяжек и
обжатия свода
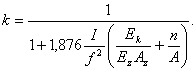
При
отсутствии затяжек коэффициент k учитывает влияние смещения опор и обжатия
свода

где A и I - площадь, см2, и
момент инерции ,см4, поперечного сечения свода;
Ek - модуль деформаций кладки свода, кг/см (Еk=0,5Е0);
Аz и
Еz - площадь, см2, поперечного сечения и
модуль упругости, кг/см2, затяжки;
D - горизонтальное смещение
опоры у пяты свода, см, при Н=1 кг;
n - коэффициент, принимаемый в зависимости от подъема свода в ключе.
f/l 1/2 1/3 1/4 1/5 1/6 1/7
n 0,554 0,696 0,785 0,843 0,881 0,911
Примечания: 1. При нагрузке от
собственного веса кладки свода принимается k=1.
2. Для сводов с отношением
стрелы подъема к пролету f/l³1/3, опирающихся на
фундаменты, при всех нагрузках принимается k=1.
РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ
ПОПЕРЕЧНЫХ СЕЧЕНИЙ СВОДОВ
|
Своды |
Расчетное сечение свода
(размеры в см)
|
Площадь поперечного
сечения А, см2 |
Положение центра тяжести
сечения у0, см |
Момент инерции сечения
относительно нейтральной оси x0-x0 I, см |
Радиус инерции сечения r, см |
Полная высота сечения
свода h, см |
Предельные пролеты сводов,
м |
||
|
b |
f0 |
d |
|||||||
|
Кирпичные |
200 |
40 |
6,5 |
1410 |
29,4 |
204000 |
12,0 |
46,5 |
12 |
|
200 |
50 |
6,5 |
1470 |
35,4 |
344000 |
15,3 |
56,5 |
15 |
|
|
200 |
60 |
6,5 |
1540 |
41,5 |
503700 |
18,1 |
66,5 |
18 |
|
|
200 |
70 |
6,5 |
1610 |
47,0 |
726400 |
21,2 |
76,5 |
21 |
|
|
Кирпичные комплексной конструкции |
200 |
70 |
6,5 |
2720 |
41,9 |
904100 |
18,2 |
76,5 |
24 |
|
Из тяжелых бетонных и природных камней |
200 |
50 |
9,0 |
2040 |
36,9 |
463600 |
15,1 |
59,0 |
15 |
|
200 |
60 |
9,0 |
2130 |
43,0 |
694700 |
16,1 |
69,0 |
18 |
|
|
200 |
70 |
9,0 |
2230 |
48,6 |
976500 |
20,9 |
79,0 |
21 |
|
Примечание. Приведенные в таблице
величины предельных пролетов установлены для сводов, перекрывающих
однопролетные здания при отношении стрелы подъема сводов к пролету f/l=1/7,
отсутствии фонарей верхнего света и сосредоточенных нагрузок при нормативной
нагрузке от пароизоляционного слоя, утеплителя, стяжки и кровли до 150 кН/м2
и снеговой нагрузки для III ветрового района.
ДЛИНА ОСИ СВОДА S
|
f/l |
1/2 |
1/3 |
1/4 |
1/5 |
1/6 |
1/7 |
|
S |
1,50l |
1,25l |
1,15l |
1,1l |
1,07l |
1,05l |
ПРИЛОЖЕНИЕ 10
СОПРОТИВЛЕНИЕ ТЕПЛОПЕРЕДАЧЕ КАМЕННЫХ СТЕН
1. Теплозащитные свойства
однородных (однослойных и многослойных стен без теплопроводных включений)
характеризуются сопротивлением теплопередаче R0, м2×°С/Вт.
2. Теплозащитные свойства
многослойных каменных стен облегченной кладки с теплоизоляционным слоем,
многослойных кирпичных панелей с теплопроводными включениями и т. п.
характеризуются приведенным сопротивлением теплопередаче ![]() , м2×°С/Вт.
, м2×°С/Вт.
3. Сопротивление
теплопередаче, приведенное сопротивление теплопередаче конструкций следует
принимать равным экономически целесообразному сопротивлению теплопередаче ![]() , но во всех случаях не менее требуемого сопротивления
теплопередаче
, но во всех случаях не менее требуемого сопротивления
теплопередаче ![]() по
санитарно-гигиеническим условиям, определяемого по формуле {l}*.
по
санитарно-гигиеническим условиям, определяемого по формуле {l}*.
* В фигурных скобках приводятся номера формул,
пунктов, приложений и таблиц СНиП II-3-79.
4. Сопротивление
теплопередаче однородных каменных стен следует определять по формулам {4} и
{5}, приведенное сопротивление теплопередаче многослойных каменных стен
облегченной кладки, многослойных кирпичных панелей с теплопроводными
включениями рассчитывается в соответствии с п. {2.8} по формулам {4}и{7} или
результатам расчета температурного поля.
5. Расчет требуемого
сопротивления теплопередаче каменных стен для заданного объекта в заданном
районе строительства выполняется в следующем порядке:
по табл. {1} устанавливают
влажностный режим помещений здания или сооружения в зимний период эксплуатации
в зависимости от относительной влажности и температуры внутреннего воздуха;
по карте прил. {l}
устанавливают зону влажности, соответствующую заданному району строительства;
по прил. {2} устанавливают
условия эксплуатации наружных ограждающих конструкций в зависимости от влажностного
режима помещений и зоны влажности;
принимают предварительное
конструктивное решение наружной каменной стены и определяют ее сопротивление
теплопередаче R0 по формулам {4} и {5} или приведенное сопротивление
теплопередаче ![]() по формулам {4} и {7} и тепловую инерцию D по формуле
{2}, принимая при этом расчетные коэффициенты теплопроводности l
и теплоусвоения S по прил. {3}, соответствующими установленным
условиям эксплуатации;
по формулам {4} и {7} и тепловую инерцию D по формуле
{2}, принимая при этом расчетные коэффициенты теплопроводности l
и теплоусвоения S по прил. {3}, соответствующими установленным
условиям эксплуатации;
по заданному району
строительства и определенному показателю тепловой инерции стены в соответствии
с п. {2.3} СНиП II-3-79 принимают расчетную зимнюю температуру наружного
воздуха tн, °С;
в формулу {l}
подставляют величины tв, tн, Dtн, aв и определяют ![]() ;
;
сравнивают ![]() с R0 или
с R0 или ![]() предварительно принятой конструкции стены. В
случае их расхождения, если это возможно, изменяют толщину стены или
теплоизоляционного слоя до размеров, обеспечивающих равенство
предварительно принятой конструкции стены. В
случае их расхождения, если это возможно, изменяют толщину стены или
теплоизоляционного слоя до размеров, обеспечивающих равенство ![]() и R0 или
и R0 или ![]() ;
;
после этого проверяют заново
соответствие показателя тепловой инерции принятой расчетной зимней температуре
наружного воздуха;
в случае их несоответствия
изменяют термическое сопротивление наружной стены, снова вычисляют его тепловую
инерцию и принимают расчетную зимнюю температуру наружного воздуха,
соответствующей откорректированному значению D.
6. Расчет экономически
целесообразного сопротивления теплопередаче ![]() наружных каменных стен выполняется в
следующем порядке:
наружных каменных стен выполняется в
следующем порядке:
определяют экономически
целесообразное термическое сопротивление однослойной стены или утеплителя в
многослойной кирпичной стене ![]() ,
м2´°С/Вт;
,
м2´°С/Вт;
предварительно определяют
экономически целесообразное сопротивление теплопередаче однородной
(однослойной) или многослойной кирпичной стены;
предварительно рассчитывают
толщину однослойной или утеплителя многослойной кирпичной стены.
По формуле {17} определяют
приведенные затраты, руб/м2, для вариантов расчета, равных или
близких величинам сопротивлений теплопередаче.
Полученные в формуле {l7} значения
приведенных затрат, руб/м2, сопоставляются, и выбирается вариант с
наименьшими приведенными затратами.
7. Результаты расчета
требуемых сопротивлений теплопередаче ![]() ,
м2×°С/Вт, наружных стен по
санитарно-гигиеническим условиям при нормативных температурных перепадах для
наружных стен разных видов зданий и помещений в зависимости от температуры
внутреннего воздуха и зимней расчетной температуры приведены в табл. 1.
,
м2×°С/Вт, наружных стен по
санитарно-гигиеническим условиям при нормативных температурных перепадах для
наружных стен разных видов зданий и помещений в зависимости от температуры
внутреннего воздуха и зимней расчетной температуры приведены в табл. 1.
Пример. Определить экономически
целесообразное сопротивление теплопередаче кирпичной стены из облегченной
кладки жилого здания, строящегося в Москве. Расчетная температура внутреннего
воздуха жилого здания принимается равной 18°С, относительная влажность воздуха
в соответствии с примечанием к п. {2.10} - равной 55%.
По принятым значениям
температуры и относительной влажности внутреннего воздуха по табл. {l}
устанавливаем, что здание эксплуатируется при нормальном влажностном режиме.
Поскольку Москва расположена на территории зоны с нормальной относительной
влажностью воздуха (прил. {1}) и эксплуатируемые помещения имеют нормальный
влажностный режим, то в соответствии с прил. {2} расчетные значения l
и S принимаем по графе Б прил. {3}.
ТРЕБУЕМОЕ СОПРОТИВЛЕНИЕ
ТЕПЛОПЕРЕДАЧЕ ![]() , м2×°С/Вт, ДЛЯ НАРУЖНЫХ СТЕН ПО
САНИТАРНО-ГИГИЕНИЧЕСКИМ УСЛОВИЯМ
, м2×°С/Вт, ДЛЯ НАРУЖНЫХ СТЕН ПО
САНИТАРНО-ГИГИЕНИЧЕСКИМ УСЛОВИЯМ
|
Здания и помещения |
Нормативный температурный
перепад Dtн, °С, для наружных стен |
Расчетная температура
внутреннего воздуха tв, °С |
Расчетные температуры
наружного воздуха tн, °С |
||||
|
-10 |
-20 |
-30 |
-40 |
-50 |
|||
|
Здания жилые, больничных учреждений (больниц,
клиник, стационаров и госпиталей), здания диспансеров и
амбулаторно-поликлинических учреждений, родильных домов, домов ребенка,
домов-интернатов для престарелых и инвалидов; учебные здания и спальные
корпуса общеобразовательных детских школ; здания детских садов, яслей,
яслей-садов (комбинатов), детских домов и детских приемников-распределителей |
6 |
18 |
0,54 |
0,73 |
0,92 |
1,11 |
1,30 |
|
|
20 |
0,57 |
0,77 |
0,96 |
1,15 |
1,34 |
|
|
|
22 |
0,61 |
0,80 |
1,00 |
1,19 |
1,38 |
|
|
Общественные здания, кроме указанных выше, и
вспомогательные здания и помещения промышленных предприятий, за исключением
помещений с влажным или мокрым режимом |
7 |
18 |
0,46 |
0,62 |
0,79 |
0,95 |
1,12 |
|
|
20 |
0,49 |
0,66 |
0,82 |
0,98 |
1,15 |
|
|
Производственные здания с сухим режимом |
10 |
12 |
0,25 |
0,37 |
0,48 |
0,60 |
0,71 |
|
|
15 |
0,29 |
0,40 |
0,52 |
0,63 |
0,75 |
|
|
|
17 |
0,31 |
0,42 |
0,54 |
0,65 |
0,77 |
|
|
|
20 |
0,34 |
0,46 |
0,57 |
0,69 |
0,80 |
|
|
|
22 |
0,37 |
0,48 |
0,60 |
0,71 |
0,83 |
|
|
Производственные здания с нормальным режимом |
8 |
12 |
0,32 |
0,46 |
0,60 |
0,75 |
0,89 |
|
|
15 |
0,36 |
0,50 |
0,65 |
0,79 |
0,93 |
|
|
|
17 |
0,39 |
0,53 |
0,68 |
0,82 |
0,96 |
|
|
|
20 |
0,43 |
0,57 |
0,72 |
0,86 |
1,00 |
|
|
|
22 |
0,46 |
0,60 |
0,75 |
0,89 |
1,03 |
|
|
Производственные здания со значительными избытками
теплоты (более 23 Вт/м3) и расчетной относительной влажностью
внутреннего воздуха не более 50% |
12 |
12 |
0,21 |
0,31 |
0,40 |
0,50 |
0,59 |
|
|
15 |
0,24 |
0,34 |
0,43 |
0,53 |
0,62 |
|
|
|
17 |
0,26 |
0,35 |
0,45 |
0,55 |
0,64 |
|
|
|
20 |
0,29 |
0,38 |
0,48 |
0,57 |
0,67 |
|
|
|
22 |
0,31 |
0,40 |
0,50 |
0,59 |
0,69 |
|
|
|
24 |
0,33 |
0,42 |
0,52 |
0,61 |
0,71 |
|
|
|
26 |
0,34 |
0,44 |
0,54 |
0,63 |
0,73 |
|
А. Исходные данные
Внутренние, наружные и
поперечные слои облегченной кладки выполнены из сплошного глиняного
обыкновенного кирпича на цементно-песчаном растворе. При этом принимаются
следующие характеристики:
g0=1800
кг/м3; l=0,81 Вт/(м×°С);
S=10,12 Вт/(м2×°С);
с теплоизоляционными
вкладышами из пеностекла
g0=200
кг/м3; l=0,09 Вт/(м×°С);
S=1,10 Вт/(м2×°С);
со штукатурным слоем с
внутренней стороны толщиной 0,02 м
g0=1600
кг/м3; l=0,7 Вт/(м×°С);
S=8,69 Вт/(м2×°С);
aв=8,7 Вт/(м2×°С); aн=23 Вт/(м2×°С);
Dtн=6 °С;
tот.пер=-3,2°С; zот.пер=217 сут.=4920 ч/год; Ст=1,1×10-9 руб/Дж (действующий прейскурант); n=0,85,
см. п. {2.14};
lт=1,3, см. п. {2.14};
Ет=0,08 (1/год), см. п. {2.14}; Сут=35 руб/м3.
Б. Порядок расчета
Экономически целесообразное
термическое сопротивление слоя теплоизоляции определяется по формуле
 м2×°С/Вт
м2×°С/Вт
Экономически целесообразное
сопротивление теплопередаче стены находим по формуле
![]() м2×°С/Вт.
м2×°С/Вт.
Толщина слоя утеплителя
определяется по формуле
![]() м
м
Для расчета принимается стена
с внутренним слоем в один кирпич, с наружным и поперечным слоями в 1/2 кирпича,
с утеплителем толщиной 0,13 м. Расстояние между поперечными слоями принимаем
1,17 м. В расчете принимается площадь размером 1,17´1,0=1,17 м2. Приведенное термическое сопротивление стены
определяется в соответствии с п. {2.8}:
а) при условном разрезании
стены плоскостями, параллельными направлению теплового потока, по формуле {6}
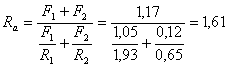 м2×°С/Вт
м2×°С/Вт
где F1 - площадь участка стены с
утеплителем, равная 1,05´1,0=1,05 м2;
F2 - площадь участка стены с
поперечными кирпичными слоями, равная 1,17-1,05=0,12 м2;
R1 - термическое сопротивление
участков стены с утеплителем
![]() м2×°С/Вт;
м2×°С/Вт;
R2 - термическое сопротивление
участков стены с поперечными кирпичными слоями
![]() м2×°С/Вт;
м2×°С/Вт;
б) условно разрезаем стены на
четыре слоя плоскостями, перпендикулярными направлению теплового потока, и
вычисляем их термическое сопротивление.
Штукатурка на внутренней
поверхности стены толщиной 0,02 м
R1=0,029 м2×°С/Вт.
Внутренний кирпичный слой
толщиной 0,25 м
R2=0,31 м2×°С/Вт.
Теплоизоляционные вкладыши из
пенопласта
![]() м2×°С/Вт.
м2×°С/Вт.
Кирпичный слой толщиной 0,13
м
![]() м2×°С/Вт.
м2×°С/Вт.
Кирпичный слой с
теплоизоляционными вкладышами из пенопласта
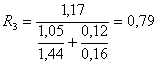 м2×°С/Вт
м2×°С/Вт
Наружный кирпичный слой
Rн=0,15 м2×°С/Вт.
Таким образом:
Rd=0,029+0,31+0,79+0,15=1,28 м2×°С/Вт.
Приведенное термическое
сопротивление стены определяем по формуле {7}:
![]() м2×°С/Вт.
м2×°С/Вт.
Приведенное сопротивление
теплопередаче R0 стены по формуле {4}:
![]() м2×°С/Вт.
м2×°С/Вт.
Аналогично определяется
приведенное сопротивление теплопередаче стен с утеплителем толщиной 6, 8, 9 и
10 см.
Приведенные затраты П, руб/м2,
определяем по формуле {17}:
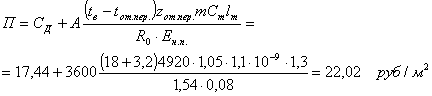
Единовременные
затраты Сд, входящие в формулу {17}, определены с учетом расхода и
стоимости материалов, затрат труда на изготовление материалов и строительство.
Аналогично определяются
приведенные затраты для кирпичных стен из облегченной кладки с утеплителем
толщиной 6, 8, 9 и 10 см.
Данные экономического расчета
приведены в табл.2.
ДАННЫЕ ЭКОНОМИЧЕСКОГО РАСЧЕТА
|
dут., см |
Ro, м2×°С/Вт |
Сд, руб/м2 |
П, руб/м2 |
|
6 |
1,07 |
14,99 |
21,57 |
|
8 |
1,21 |
15,69 |
21,52 |
|
9 |
1,29 |
16,04 |
21,52 |
|
10 |
1,35 |
16,39 |
21,63 |
|
13 |
1,54 |
17,44 |
22,02 |
На основании итоговых данных
экономического расчета принимается наружная стена из облегченной кладки с
утеплителем толщиной 8 см.
Для зданий с поперечными несущими
стенами высотой до 9 этажей включ. при расчетной температуре наружного воздуха
до минус 40°С рекомендуется принимать толщину каждого из продольных слоев
облегченной кладки в полкирпича.
ПРИЛОЖЕНИЕ 11
РАСЧЕТ КОНСТРУКЦИЙ КАМЕННЫХ ЗДАНИЙ
НА ТЕМПЕРАТУРНО-ВЛАЖНОСТНЫЕ
ВОЗДЕЙСТВИЯ И УСАДКУ
ОБЩИЕ УКАЗАНИЯ
1. Расчет конструкций
каменных зданий на температурно-влажностные воздействия и усадку выполняется в
случаях, когда длина зданий или расстояния между температурными швами превышают
указанные в п. [6.79].
2. Каменные здания
представляют собой сложное сочетание конструкций из различных материалов, с
разными физико-механическими свойствами: армированной и неармированной кладок
(стен, столбов, сводов) и стальных или железобетонных элементов (балок,
перемычек, перекрытий, затяжек, поясов и т. п.), которые в отличие от каменных
кладок могут воспринимать значительные растягивающие усилия.
Неармированные кладки плохо
работают при растяжении, в связи с чем в них при понижении температуры и усадке
могут возникать трещины, появление которых трудно предотвратить обычными
мерами. Поэтому расчет каменных конструкций на действие температуры и усадки
производится на прочность и деформативность с учетом возможности появления и
раскрытия в период эксплуатации трещин, безопасных для прочности, долговечности
и надежности конструкций зданий.
В связи с этим расчет
конструкций на действие температуры по раскрытию трещин производится только для
периода эксплуатации здания. Для строительного периода расчет конструкций
производится, в основном, на прочность. Расчет по раскрытию трещин в этом
случае является необязательным в связи с кратковременностью этого периода.
Допустимые величины раскрытия
трещин в армированных и неармированных кладках в период эксплуатации здания
приводятся в табл. 1.
3. Конструкции каменных
зданий рассчитываются на наиболее неблагоприятный случай работы кладки -
растяжение, которое возникает при понижении температуры (зимой) и при усадке.
Расчет производится в упругой стадии на расчетные изменения средних приведенных
температур сечения Dt и
перепадов температур по толщине Dq
с учетом влияния колебаний влажности воздуха, солнечной радиации и усадки,
которые могут быть как в период строительства, так и эксплуатации здания.
Расчетные значения средних температур Dt и Dq определяются в соответствии
с указаниями пп. 7-8 приложения.
4. Расчет на действие
температуры Dt
производится при определении продольных сил и перемещений в плоскости
конструкций; расчет на действие температуры Dq
производится для определения усилий и перемещений конструкций при их
искривлении или изгибе из плоскости.
При одновременном действии
температур Dt и Dq (например, для наружных стен
отапливаемых зданий) соответствующие усилия и перемещения складываются на
основании принципа независимости действия сил.
5. При образовании в
неармированной кладке стен сквозных трещин расчетная схема здания (при наличии
сборных перекрытий) может изменяться, так как при этом здание разделяется на
отдельные несвязные блоки (черт.
1, а, в). В армированных стенах образование трещин обычно не изменяет расчетную схему,
изменяются только жесткостные характеристики стен и перекрытий (продольная и
изгибная жесткость и т.п.).
ДОПУСТИМОЕ РАСКРЫТИЕ
ТЕМПЕРАТУРНО-УСАДОЧНЫХ
ТРЕЩИН, ММ, В НЕАРМИРОВАННЫХ И АРМИРОВАННЫХ
КЛАДКАХ ВСЕХ ВИДОВ В ПЕРИОД ЭКСПЛУАТАЦИИ ЗДАНИЙ
|
Конструкции |
Стены |
|||
|
наружные |
внутренние |
|||
|
неармированные |
армированные |
неармированные |
армированные |
|
|
Несущие столбы и простенки |
Не допускаются |
0,4 (0,3) |
Не допускаются |
0,5 (0,3) |
|
Поперечные и продольные стены в местах опирания
перекрытий |
0,5+dc£1,5 (1) |
0,4 (0,3) |
0,5+dc£1,5 (1) |
0,5 (0,3) |
|
Сплошные (без проемов) участки стен длиной 3 м и
более; межоконные пояса, цоколи, фронтоны |
1+dc£2 (1,5) |
0,4 (0,3) |
1+dc£2 (1,5) |
0,5 (0,3) |
|
Кладка стен, пилястр в местах опирания
большепролетных (l>6 м) ферм, балок, прогонов и т. п. |
Не допускаются |
0,4 (0,2) |
Не допускаются |
0,4 (0,2) |
Примечания: 1. Цифры без скобок
относятся к зданиям с нормальным температурно-влажностным режимом эксплуатации,
в скобках - с влажным и мокрым режимами.
2. Указанные в таблице
допуски могут быть изменены при соответствующем обосновании, например, на
основании использования опыта эксплуатации аналогичных конструкций.
3. dc - раскрытие трещин при
усадке определяется по формуле
(73) приложения.
Под армированной кладкой понимается кладка, содержащая непрерывную продольную арматуру как в виде отдельных стержней (армокирпичные пояса, рядовые перемычки), так и в виде арматуры железобетонных и стальных включений (балок, поясов, плит перекрытий, заделанных в стены и т. п.), которые при растяжении и сжатии работают совместно с кладкой.

Черт. 1.
Расчетные схемы многоэтажных зданий с
регулярной конструктивной схемой
а - фасад; б - здание с поперечными несущими стенами и сборными перекрытиями (I тип); в - то же, с продольными несущими стенами (II тип); г - поперечное сечение здания I и II типов
В противном случае кладка
считается неармированной.
6. Расчет каменных
конструкций на температурные воздействия следует выполнять для двух стадий
работы кладки: до образования в кладке трещин первая стадия), когда максимальные
растягивающие напряжения sk,max не превышают временного сопротивления кладки при
растяжении по перевязанному сечению Rtu=2,25Rt:
sk,max£Rtu (1)
и после образования трещин
(вторая стадия), когда
sk,max>Rtu (2)
где Rt - расчетное сопротивление
кладки растяжению по перевязанному сечению, проходящему по кирпичу или камню,
см. табл. [10].
РАСЧЕТНЫЕ ТЕМПЕРАТУРЫ
КОНСТРУКЦИЙ Dt
И Dq
7. Расчетные значения
приведенных средних температур Dt и Dq для наружных и внутренних
конструкций отапливаемых и неотапливаемых зданий в строительный и
эксплуатационный периоды определяются по формулам (3)-(8) табл.2 приложения.
8. Эквивалентная температура
усадки многослойного (комплексного) сечения, состоящего из слоя кладки (k) и бетонного
или железобетонного (b) включений (перемычки), при
приведении к показателям кладки вычисляется по формуле
![]() (10)
(10)
где ak, ab - коэффициенты
температурного расширения кладки и бетона;
tc,k, tc,b -
эквивалентные температуры усадки кладки и бетона, принимаемые по табл. 3 приложения;
Кk,
Кb - продольные жесткости кладки и бетона определяют по
пп. 23-30 приложения.
ЖЕСТКОСТНЫЕ ХАРАКТЕРИСТИКИ
ЭЛЕМЕНТОВ
КАМЕННЫХ И ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
Продольная жесткость и
податливость стен и перекрытий
9. Продольная жесткость при
растяжении и сжатии монолитной (без трещин) кладки k или бетона b при
работе в первой стадии определяется по формулам:
для неармированной кладки (черт. 2, a)
Kk=EkAk; Kb=EbAb; (11)
для армированной кладки
(черт. 2, б)
Ksk=EkAk+EsAs; (12)
для
комплексного сечения (кладка с монолитным железобетонным включением без трещин,
черт.2, в)
Ksk=EkAk+EbAb+EsAs; (13)
где Еk=0,5Е0
- модуль деформаций кладки;
Еb=0,5Еb -
модуль деформации бетона;
Е0, Еb, Еs -
начальные модули упругости кладки бетона и арматуры;
Аk, Ab, As - расчетные площади сечения монолитной кладки,
бетона и арматуры, определяемые в соответствии с указаниями п. 13 приложения.
РАСЧЕТНЫЕ ЗНАЧЕНИЯ
ПРИВЕДЕННЫХ СРЕДНИХ ТЕМПЕРАТУР
|
Период, здание |
Конструкции |
Расчетные температуры, °С |
Формулы |
|
Эксплуатационный, отапливаемое |
Наружные стены |
Dt |
0,5[0,5(tm,s,min+tf,n)-tm,s,max]-Aw-tc
(3) |
|
Dq |
tf,n-tm,s,min
(4) |
||
|
Внутренние стены и перекрытия |
Dt |
0,5(tf,n-tm,s,max)-tc
(5) |
|
|
То же, неотапливаемое |
Наружные и внутренние стены |
Dq |
0,5(tm,s,min-tm,s,max)-Aw-tc
(6) |
|
Строительный, неотапливаемое |
Наружные и внутренние стены и перекрытия |
Dt |
tm,s,min-0,8tm,m,max-Aw-0,5tc
(7) |
|
Dq |
0 (8) |
Обозначения, принятые в табл. 2:
tm,s,max, tm,s,min - максимальная (июльская) и минимальная (январская)
среднесуточные температуры наружного воздуха (наиболее жаркие и холодные сутки)
принимаются по СНиП 2.01.01-82;
tm,m,max - среднемесячная температура
наружного воздуха, в июле принимается во СНиП 2.01.01-82;
tf,n - температура, внутреннего воздуха зимой (для жилых
помещений tf,n=18°С);
Aw, tc
- соответственно эквивалентные температуры сорбционного увлажнения (при колебаниях
относительной влажности воздуха) и усадка монолитных и сборных неармированных
бетонных и каменных конструкций принимаются по табл. 3; эквивалентная усадка для армированных каменных и
бетонных конструкций определяется по формуле
tc,s=(1-mm)tc, (9)
где m - процент армирования бетона
или кладки;
m=0,2 - принимается для
бетона класса ³В7,5;
m=0,5 - принимается для
бетона класса <В7,5 и всех видов кладки.
УСАДКА БЕТОННЫХ И КАМЕННЫХ
КОНСТРУКЦИЙ
|
Материал конструкций |
Аw,
°С |
Усадка tc, °С, конструкций |
||
|
побережье и острова
Ледовитого и Тихого океанов |
континентальные районы
СССР |
монолитных |
сборных |
|
|
Бетон |
4 |
-5 |
40 |
20 |
|
Кладка из силикатного кирпича (блоков) |
4 |
-7 |
30 |
15 |
|
Кладка из камней легкого и ячеистого бетонов
(блоков) |
8 |
-10 |
30 |
15 |
|
Кладка из глиняного кирпича (блоков) |
0 |
0 |
0 |
0 |
10. Продольная жесткость
армированной кладки или бетона с трещинами при растяжении
Ksk(b)=EsAs/ys. (14)
То же, для комплексного
сечения (монолитная кладка без трещин и железобетонное включение с трещинами -
сборные перемычки, балки и т. п., см. черт. 2, в)
Ksk=EkAk+EsAs/ys, (15)
где ys -
коэффициент, учитывающий работу армированной кладки или бетона на участке между
трещинами, принимаемый равным: для растворов и бетонов класса В2 и выше ys=0,7;
для менее прочных растворов и бетонов (меньше В2) ys=l.
11. Податливость li и коэффициент податливости Сi
неармированных, армированных кладок и комплексных сечений элементов с трещинами
и без трещин определяются по формулам:
li=1/Кi, (16)
Сi=li/Кi, (17)
Черт. 2. Определение
продольной жесткости неармированной и армированной кладок
а - неармированная кладка; б
- армированная кладка; в - кладка с железобетонным включением
где li - длина элемента;
Ki - продольная жесткость элемента, определяемая по формулам (11)-(15) приложения, где i
принимает значения: для кладки - k; для бетона - b; для
армированной кладки - sk.
12.
Расчетные
площади сечения монолитной (без трещин) кладки Аk бетона Аb и
арматуры Аs определяются в пределах рассматриваемого участка
зоны влияния продольной силы N длиной l,
возникающей в элементах стен и перекрытий при растяжении или сжатии, см. черт. 3 (заштриховано). Зона
влияния силы N на длине li рассматриваемого участка
имеет криволинейное очертание. Для упрощения расчетов криволинейное очертание
зоны приближенно заменяется треугольным (пунктир) с углом в основании 45° и
высотой, равной половине длины основания. Для каменных и бетонных конструкций,
однородных по материалу или армированию, треугольное очертание зоны можно
заменить равновеликим по площади прямоугольным (штрихпунктир). Высота или длина
прямоугольной зоны определяется из равенства площадей прямоугольной и
треугольной или трапецеидальной зон.
При приведении треугольной
зоны к прямоугольной при неизменном основании высота прямоугольной зоны
принимается равной 1/4 длины основания (см. черт. 3). Высота прямоугольной зоны не должна превышать
половину высоты этажа.
При приведении
трапецеидальной зоны к прямоугольной при неизменной высоте заштрихованного
участка длина прямоугольной зоны принимается равной полусумме верхнего и
нижнего основания трапеции.
СРЕДНЯЯ ПРОДОЛЬНАЯ ЖЕСТКОСТЬ
РАСЧЕТНОГО СЕЧЕНИЯ СТЕНЫ,
ПЕРЕКРЫТИЯ И ЭТАЖА
13.
Средняя
продольная жесткость расчетного сечения наружной (е), внутренней (f) стен и
перекрытия (р) в пределах этажа в общем случае определяется по формуле

Черт. 3. Примеры построения зон влияния продольной силы N в кладке стен перекрытий
а - в стенах при отсутствии трещин; б - то же, при наличии трещин; в - в плитах перекрытий, опертых на стены; г - в поперечной стене или простенке
где L - длина здания;
n - число
одинаковых по конструкции участков (см. черт. 2), на которые разбивается по длине стена или перекрытие
(см. черт. 3);
сi -
коэффициент податливости i-го участка стены или
перекрытия длиной li определяемый по формуле (17).
14. Средняя продольная
жесткость расчетного сечения этажа определяется по формулам:
для здания I типа (см. черт. 1, б)
K=Ke(A)+Kf(Б)+Ke(В)+Kр; (19)
для здания II типа
(см. черт. 1, в)
K=Ke(A)+Kp(A) и т. д., (20)
где в скобках обозначены оси
стен.
ИЗГИБНАЯ ЖЕСТКОСТЬ
КОНСТРУКЦИЙ
15. Изгибная жесткость
сечения неармированной монолитной кладки без трещин (I стадия) определяется по
формуле
Вk=EkIk=Ekh,kd3k/12, (21)
где Ik - момент инерции сечения
Ik=hkd3k/12; (22)
соответствующий момент
сопротивления сечения
Wk=hkd2k/6, (23)
где hk, dk - ширина (высота) и толщина
сечения.
16. Изгибная
жесткость сечения армированной монолитной кладки без трещин (I стадия)
определяется по формуле
Bsk=EkIsk, (24)
где Isk - приведенный момент инерции
сечения армированной кладки без трещин (черт. 4), определяемый по формуле
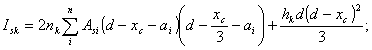 (25)
(25)
xc - высота сжатой зоны кладки (бетона), определяемая по формуле
 (26)
(26)
nk=Е0/Еb, (27)
где Аsi
- площадь сечения арматуры i-го ряда (сжатой и
растянутой);
ai - расстояние от оси арматуры i-го ряда до растянутой грани
сечения кладки.
Соответствующий момент
сопротивления сечения армированной кладки равен
Wsk=Isk/(d-xc). (28)
17. Изгибная жесткость
сечения армированной кладки с трещиной (II стадия) определяется по формуле
где ![]() (30)
(30)
 (31)
(31)
Соответствующий момент сопротивления
сечения
Wsy=Isy/(d-xc/3-ai). (32)
Изгибная жесткость
железобетонных и бетонных элементов определяется по формулам (21)-(32), заменяя в них Еk и
nk на Еb и nb= Es/Eb.
Черт. 4.
Определение изгибной жесткости, сечения
армированной кладки с трещиной
СДВИГОВАЯ ЖЕСТКОСТЬ СТЕН
18. Приведенная сдвиговая
жесткость элементов каменных стен типа двутавра (черт. 5) или сплошных пластин
при отсутствии вертикальных трещин в перемычках или углах проемов вычисляется
по формулам:
для двутаврового сечения (см.
черт. 5)
для прямоугольных пластин
Dk=GkAk»EkAk/3; (34)
при наличии трещин в
перемычках или углах проемов (hk=0; h0=h)
где h0, hk, h - высота проема, пояса
кладки и этажа;
I0, A0 - момент инерции сечения и
площадь сдвига стен в уровне простенков, вычисляемые по формулам:
для двутаврового сечения (см.
черт. 5)
![]() (36)
(36)
A0=d1b1+d2b2+cB0;
для прямоугольного сечения d/b
![]() А0=db; (37)
А0=db; (37)
k -
коэффициент, учитывающий жесткость заделки верха и низа простенка: при жесткой
заделке (без учета изгиба перемычек) k=12; при податливой заделке
(с учетом изгиба перемычек) k=8;
Аk -
площадь сдвига поясов стен выше и ниже проемов, вычисляемая по формулам:
для двутаврового сечения, см.
черт. 5
![]() (38)
(38)
для прямоугольного сечения
![]() (39)
(39)
где lm, lm+1 - расстояние между осями
поперечных стен или простенков слева и справа от рассматриваемой оси.
Черт. 5. Определение сдвиговой жесткости наружных и внутренних стен этажа
19. Средняя погонная
сдвиговая жесткость этажа или отдельной стены в пределах этажа вычисляется по
формуле
![]() (40)
(40)
где Di - сдвиговая жесткость i-го
элемента этажа, определяемая по формулам (33)-(35);
L - длина
этажа;
n - число
элементов по длине этажа.
ПРИВЕДЕННАЯ ВЫСОТА ЭТАЖА И
ЗДАНИЯ
20. Приведенная высота этажа
определяется по формуле
![]() (41)
(41)
где h - фактическая высота этажа;
K, D -
средние продольная и сдвиговая погонные жесткости этажа, определяемые по формулам (19), (20), (35).
21. Приведенная высота здания
(стены) определяется по формуле
![]() (42)
(42)
где h0,i -
приведенная высота i-го этажа;
р - число этажей, включая
подвальное и чердачное помещения.
22. Для зданий с регулярной
конструктивной схемой (см. черт. 1)
при высоте этажей не более 4 м приведенная высота этажа h0 может приближенно
приниматься равной его фактической высоте, т. е. h0»h.
ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРНЫХ УСИЛИЙ
В СТЕНАХ И ПЕРЕКРЫТИЯХ ЗДАНИЙ
23.
Продольные
усилия в стенах и перекрытиях зданий возникают вследствие заделки конструкций в
фундаменты, которые стесняют их температурные деформации (см. черт. 1), а также при наличии разности
температурных деформаций сопряженных элементов.
В каждом отдельном случае
расчет усилий представляет собой сложную статическую задачу, схемы решения
которой могут быть разнообразными. В зависимости от конструктивной схемы,
планировки и этажности здания его конструкции (стены и перекрытия) могут
рассчитываться на действие температуры Dt как
рамы, составные стержни или пластинки (черт. 6), заделанные в основание (фундаменты), подвижностью
которых можно пренебречь. При этом возможны два типа расчетных схем:
1 тип - здания с продольными
стенами, с монолитными или сборными перекрытиями, работающими при растяжении и
сжатии как одно сечение (см. черт. 1,
б, г), при этом здание рассчитывается как пространственная система (коробчатый
брус);
П тип - здания с частой
поперечной разрезкой перекрытий - сборные плиты (см. черт. 1, в, г), которая исключает совместную работу
продольных стен друг с другом; при этом расчетная схема здания распадается на
отдельные плоские системы, включающие элементы продольных стен и участки
перекрытий, вовлекаемых при растяжении в совместную работу со стенами, см. черт. 1, в (заштриховано) .
24. Расчет
каменных зданий как рамных или стоечно-связевых систем (см. черт. 6, б, в) выполняется методом сил или
деформаций, что приводит к решению систем алгебраических уравнений с большим
числом неизвестных. Решение таких систем оказывается возможным только с
применением ЭВМ.
Черт. 6. Расчетные схемы каменных зданий
а - как квазиизотропных пластинок;
б, в - как стержневых систем (рам)
При решении методом сил рам (n раз
статически неопределимых) температурные усилия (моменты М, продольные N и
поперечные Q силы) находятся из решения системы канонических
уравнений:
где i=1, 2, 3 ...,
Коэффициенты при неизвестных dik вычисляются с учетом
продольных и сдвиговых (для массивных стержней типа простенков) деформаций по
формуле
Свободные (температурные)
члены Dit вычисляются по формуле
25. При расчете на действие
температуры зданий с регулярной конструктивной схемой как квазиизотропной
пластинки с приведенными геометрическими и физико-механическими
характеристиками суммарные продольные усилия в наружных е, внутренних f стенах
и перекрытиях р зданий I типа (см. черт.
1, б) для m-го сечения этажа вычисляются по формулам:
а) в наружной стене
Ne,m=nmaeKeDte+DNm; (46)
б) во внутренней стене при Dtf=Dtp
![]() (47)
(47)
в) в перекрытии (47)
где DNm - дополнительное усилие, возникающее в стенах и перекрытиях при их
взаимодействии (силы сдвига), вычисляется по формуле
Кe, Кf,
Кр - средние продольные жесткости расчетного сечения наружной и
внутренней стен и перекрытия в пределах этажа, определяемые по формуле (18);
К - то же, всего этажа,
определяемые по формуле (19);
ae, af, ap -
коэффициенты температурного расширения материала наружных, внутренних стен и
перекрытий;
для составных сечений,
состоящих из нескольких материалов (см. черт. 2, в) с различными физико-механическими
свойствами, приведенный коэффициент ared вычисляется по формуле
где aiKi - коэффициент температурного расширения и жесткость i-го
слоя;
Dte, Dtf, Dtp - расчетные средние температуры наружных, внутренних стен и перекрытий,
вычисляемые по формулам
(3)-(8);
nm - коэффициент, учитывающий влияние задела стен в основание;
для точки m с
относительными координатами x=x/L и z=у/Н0
(см. черт. 6, a) nm определяется по формулам (51)-(57) или по табл. 4 для заданного отношения L/H0:
КОЭФФИЦИЕНТЫ nx ДЛЯ ТОЧЕК С ОТНОСИТЕЛЬНЫМИ КООРДИНАТАМИ x=x/L И z=у/Н
ПЛАСТИН С
РАЗЛИЧНЫМ ОТНОШЕНИЕМ СТОРОН L/H
|
L H |
|
z=у/Н |
||||||
|
0 |
0,1 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
||
|
1 |
0 |
0,903 |
0,685 |
0,468 |
0,182 |
0,047 |
-0,030 |
-0,124 |
|
0,1 |
0,902 |
0,673 |
0,451 |
0,172 |
0,044 |
-0,029 |
-0,119 |
|
|
0,2 |
0,898 |
0,632 |
0,399 |
0,144 |
0,036 |
-0,025 |
-0,101 |
|
|
0,3 |
0,886 |
0,540 |
0,301 |
0,101 |
0,025 |
-0,018 |
-0,074 |
|
|
0,4 |
0,845 |
0,339 |
0,159 |
0,051 |
0,012 |
-0,010 |
-0,039 |
|
|
0,5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
2 |
0 |
0,888 |
0,796 |
0,675 |
0,457 |
0,282 |
0,148 |
0,047 |
|
0,1 |
0,887 |
0,790 |
0,664 |
0,442 |
0,269 |
0,139 |
0,039 |
|
|
0,2 |
0,885 |
0,769 |
0,625 |
0,391 |
0,229 |
0,113 |
0,020 |
|
|
0,3 |
0,876 |
0,716 |
0,535 |
0,297 |
0,164 |
0,077 |
0,001 |
|
|
0,4 |
0,840 |
0,558 |
0,336 |
0,156 |
0,083 |
0,038 |
-0,006 |
|
|
0,5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
3 |
0 |
0,904 |
0,853 |
0,777 |
0,632 |
0,511 |
0,422 |
0,372 |
|
0,1 |
0,902 |
0,849 |
0,768 |
0,617 |
0,492 |
0,400 |
0,344 |
|
|
0,2 |
0,896 |
0,833 |
0,738 |
0,567 |
0,433 |
0,334 |
0,267 |
|
|
0,3 |
0,882 |
0,793 |
0,666 |
0,461 |
0,326 |
0,234 |
0,159 |
|
|
0,4 |
0,843 |
0,672 |
0,475 |
0,265 |
0,172 |
0,116 |
0,062 |
|
|
0,5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
4 |
0 |
0,925 |
0,900 |
0,852 |
0,760 |
0,686 |
0,634 |
0,611 |
|
0,1 |
0,921 |
0,894 |
0,843 |
0,744 |
0,663 |
0,606 |
0,578 |
|
|
0,2 |
0,910 |
0,876 |
0,814 |
0,692 |
0,593 |
0,519 |
0,475 |
|
|
0,3 |
0,891 |
0,839 |
0,749 |
0,585 |
0,463 |
0,375 |
0,308 |
|
|
0,4 |
0,846 |
0,736 |
0,576 |
0,364 |
0,255 |
0,189 |
0,125 |
|
|
0,5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
6 |
0 |
0,953 |
0,955 |
0,941 |
0,906 |
0,879 |
0,861 |
0,854 |
|
0,1 |
0,948 |
0,948 |
0,931 |
0,890 |
0,857 |
0,836 |
0,827 |
|
|
0,2 |
0,933 |
0,927 |
0,900 |
0,839 |
0,788 |
0,752 |
0,735 |
|
|
0,3 |
0,905 |
0,887 |
0,839 |
0,736 |
0,649 |
0,584 |
0,542 |
|
|
0,4 |
0,850 |
0,798 |
0,696 |
0,513 |
0,393 |
0,312 |
0,241 |
|
|
0,5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
10 |
0 |
0,968 |
0,982 |
0,987 |
0,986 |
0,983 |
0,980 |
0,979 |
|
0,1 |
0,965 |
0,979 |
0,983 |
0,980 |
0,974 |
0,970 |
0,969 |
|
|
0,2 |
0,954 |
0,966 |
0,965 |
0,952 |
0,938 |
0,929 |
0,926 |
|
|
0,3 |
0,927 |
0,930 |
0,917 |
0,877 |
0,840 |
0,813 |
0,802 |
|
|
0,4 |
0,858 |
0,845 |
0,801 |
0,688 |
0,588 |
0,513 |
0,460 |
|
|
0,5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
где v - коэффициент Пуассона;
L=2l, Н -
длима и высота здания.
26. Для здании II типа
(см. черт. 1, в, г)
суммарное продольное усилие в m-м сечении наружной е и
внутренней f стены вычисляются по формуле
Ne(f),m=nm(ae(f)Ke(f)Dte(f)+apKpDtp). (58)
27. Усилия Ne(f),m и Np,m
распределяются между отдельными элементами составного сечения стен или
перекрытий пропорционально их продольной жесткости. Например, для сечения на черт. 2, в усилия в поясе кладки k и
перемычке r соответственно равны (индекс m
опущен):
28. Усилия в плитах
перекрытий лоджии, балконов и т. п., расчетные температуры которых Dtp,b отличаются от температуры перекрытий внутри
помещений Dtp вычисляются по формуле
где Kp,b -
продольная жесткость плит перекрытий лоджий и т. п.
ВЛИЯНИЕ ОТВЕРСТИЙ И ШТРАБ
29. Температурные усилия в
стенах и перекрытиях в местах ослабления их отверстиями, штрабами, швами (черт. 7) определяются из условия
равновесия сил и моментов по неослабленному 1-1 и ослабленному 2-2 сечениям.
В монолитных перекрытиях с
замкнутым отверстием (см. черт. 7,
а) продольные усилия справа Np1 и слева Np2
от отверстия определяются по формулам:
![]()
где Np - суммарное продольное
усилие в перекрытии по неослабленному сечению по формуле (48);
b1, b2 - ширина перекрытия справа и
слева от отверстия;
B0 - ширина перекрытия в свету;
b0 - ширина отверстия.
Продольные усилия Nc1 и
Nc2 в кладке, ослабленной отверстиями,
дымовентиляционными каналами и т. п. (см. черт. 7, в) определяются по формуле (61) заменой Np, B0, b0, b1 и b2 на Nc, d, d0, d1 и d2.
При ослаблении кладки штрабой
(см. черт. 7, в) напряжение в
кладке по ослабленному сечению s¢k
определяется по формуле
где Nc - продольное усилие в стене,
определяемое по формулам
(46), (47);
е - эксцентриситет силы Nc;
A1, W1 - расчетная площадь и момент
сопротивления ослабленного сечения.
Черт. 7. К расчету продольных усилий в стенах и перекрытиях в местах ослабления отверстиями, штрабами и швами
а - перекрытие с отверстием;
б - кладка стены с отверстием; в - то же, со штрабой; г - лестничная клетка
30. Усилия Nc(B) в продольных стенах лестничных клеток (черт. 7, д) при опирании перекрытий
на поперечные стены определяются по формулам:
а) при сборном перекрытии
б) при монолитном перекрытии
![]() (64)
(64)
где be - расчетная длина лестничной
клетки;
qp=Np/B0 - распределенное погонное
температурное усилие (по неослабленному сечению перекрытия, черт. 7, а, где B0 - ширина перекрытия).
РАСЧЕТ КЛАДКИ И УЗЛОВ
СОПРЯЖЕНИЯ ПО ПРОЧНОСТИ И РАСКРЫТИЮ ТРЕЩИН
Напряжения в кладке
31. Максимальные
растягивающие напряжения в монолитной кладке без трещин при одновременном
действии продольной силы N и перепада температуры по толщине Dq (наружные стены отапливаемых
зданий) равны сумме абсолютных значений (без учета знака) соответствующих
напряжений:
sk,max=skN+skq. (65)
где skN,
skq - напряжения, возникающие в
кладке при действии силы N и перепада Dq,
равные соответственно:
skN=Nk/Ak;
skq=Mkq/Wk. (66)
32. Максимальные
растягивающие напряжения в поясе монолитной кладки без армированных включений
(см. черт. 2, а) при действии Nk и Dq
равны:
то же, по концам перемычек и
балок, заделанных в кладку и нагруженных силами Nr,m-1
и Nr,m (черт. 8, а) при ширине простенков более 40см:
Черт. 8.
Напряженно-деформированное состояние простенка в местах заделки в него
элементов
а - железобетонных или
стальных; б - армокирпичных
где dk, dr - толщина стены и ширина
перемычки;
Bk, Br,y - изгибная жесткость
монолитной кладки без трещины и железобетонной перемычки с трещинами
определяются по формулам
(21) и (29);
то же, по концам арматурных
стержней, заделанных в кладку простенков шириной более 40 см на высоту 2h (черт. 8, б):
 (69)
(69)
при ширине простенков менее 3
м в формулах (61) и (62) можно принять Nm»Nm-1
(исключая лестничные клетки).
Напряжения в арматуре
33. Напряжения в крайних
(первых) стержнях растянутой арматуры кладки с трещинами при наличии перепада
температуры по толщине Dq
определяются по формулам:
а) при отсутствии прогибов
стен внутрь (здания с жесткими перекрытиями, заделанными в стены, черт. 1, в и т. п.)
б) при прогибах стен внутрь
(нежесткие перекрытия или если перекрытия не заделаны в стены, черт. 1, б, или имеется точечное
опирание в местах заделки балок, прогонов и т. п.)
ak(b) -
коэффициент температурного расширения кладки (k) или железобетонных
перемычек (b),
ls - расчетная длина анкеровки арматуры в кладку в местах образования
трещин принимается равной расстоянию между поперечными стержнями (черт. 9), но не более толщины стены;
ly - длина прогибаемого участка монолитной кладки между трещинами,
образующимися в местах опирания стен на поперечные стены, рамы, балки
перекрытий, заделанные в стены, а также по концам железобетонных и стальных
включений в кладку (перемычки, плиты перекрытий и т. п.); для сплошных стен без
армирования включений lу=3dk;
Bsy - изгибная жесткость армированной кладки в сечении с трещиной,
определяется по формуле (29);
Bsk - тo же, монолитной кладки, определяется по формуле (24).
34. Расчетная длина заделки
(анкеровки) в кладку с трещинами стержней арматуры lc при одностороннем растяжении
силой (см. черт. 9, a) должна
быть не менее:
lc=3,2N/Rtudk. (72)
Черт. 9. Работа армированной кладки при образовании трещин в местах заделки армированных элементов
а - при односторонней
заделке; б - при двухсторонней заделке
Раскрытие трещин
35. Раскрытие
температурно-усадочных трещин в конструкциях из армированной и неармированной
кладки в период эксплуатации не должно превышать размеров, приведенных в табл. 1. Раскрытие трещин при усадке
dс вычисляется по формуле
dс=alytc, (73)
где tc определяется по табл. 3.
36. При раскрытии трещин
больше указанного в табл. 1
кладку следует армировать по расчету. Площадь сечения продольной арматуры
определяется по формулам
(70) и (71),
принимая ss1=Rs.
37. Раскрытие трещин в неармированной
кладке стен снаружи при одновременном действии температур Dt и Dq
(наружные стены отапливаемых зданий) определяется по формулам:
а) без армированных включений
где lу»3dk;
б) то же, по концам перемычек
или балок, заделанных в кладку (см. черт.
9),
где lm - расстояние между осями
простенков или стен, черт. 8, a;
lr - длина перемычки, балки, плиты и т. п.;
ared
- приведенный коэффициент температурного расширения составного сечения, черт. 2, в, вычисляемый по формуле (50).
38. Раскрытие трещин в
армированной кладке стен снаружи de
при одновременном действии температур Dt и Dq определяется по формулам:
а) без армированных включений
где ls принимается равным
расстоянию между поперечными стержнями продольной арматуры (см. черт. 9), но не более толщины стены;
б) то же, по концам перемычек
или балок, заанкеренных в кладку (см. черт.
9),
![]() (77)
(77)
39. Раскрытие трещин в кладке
стен неотапливаемых зданий и внутренних стен отапливаемых зданий определяется
по формулам (74)-(77)
при Dq=0.
Пример 1. Расчет конструкций
девятиэтажного кирпичного жилого дома с поперечными несущими стенами на
температурно-влажностные воздействия.
Расчет девятиэтажного жилого
дома производится на температурно-влажностные воздействия для периода
эксплуатации здания.
Район строительства - Москва.
КОНСТРУКЦИИ
Здание
девятиэтажное, кирпичное, с поперечными несущими стенами, с опиранием на них
плит перекрытии (I типа) длиной 108,8 м, шириной 14,4 м, высотой 28,6 м, высота
этажа - 2,8 м (черт. 10).
Наружные и внутренние стены
из глиняного кирпича пластического прессования марки 100 на растворе марки 50.
Перемычки над проемами
наружных стен сборные железобетонные размером 4´12´14 см из бетона класса В15.
Перекрытия из сборных
железобетонных плит шириной 0,8 и 1,2 м с круглыми пустотами из бетона класса
В15, заделанные в кладку стен.
РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ
МАТЕРИАЛОВ СТЕН И ПЕРЕКРЫТИЙ
Кладка стен из глиняного
кирпича марки 100 на растворах марки 50: расчетное сопротивление сжатию R=1,5
МПа, растяжению по перевязанному сечению Rt=0,18 МПа, временное
сопротивление сжатию Ru=3 МПа, растяжению – Rtu=2,25 Rt=0,4 МПа, модуль деформаций кладки Еk=0,5E0=0,5×3000=1500 МПа, где Е0=aRu=1000×3=3000 МПа; коэффициент
температурного расширения a=0,5×10-5 (1/°С).
Сборные железобетонные
перемычки наружных стен: бетон класса В15; Eb=20000 МПа; Аs=4×1,13=4,52 см2; n=Es/Eb=10,5; a=10-5
(1/°С).
Сборные железобетонные плиты
перекрытий: бетон класса В15; Еb=20000 МПа; Еs=2×105 МПа (А-Ш); n=10; a=10-5
(1/°С) армирование Аs: плита Р1 площадью 5,6 см2;
Р2 - 4 см2; Р3=2 см2: Р4=2,6 см2.
РАСЧЕТНЫЕ ТЕМПЕРАТУРЫ
Расчетные значения
приведенных средних температур Dt, Dq и усадки tc для периода эксплуатации здания принимаются:
для наружных стен - Dte=-17 °С; Dqe=50°С; tc=0°С;
для внутренних перекрытий Dtp=-23 °С; Dqp=0°С; tc=-18°С;
то же, лоджий Dtp,b=-42 °С; Dqp=0°С; tc=-18°С.
ЖЕСТКОСТНЫЕ ХАРАКТЕРИСТИКИ
СТЕН
И ПЕРЕКРЫТИЙ ПРИ ОТСУТСТВИИ В КЛАДКЕ ТРЕЩИН
Здание имеет регулярную
конструктивную схему. В связи с этим достаточно рассмотреть жесткостные
характеристики одной (средней) секции длиной L/4=27,2 м.
Наружные стены
1. Средняя продольная
жесткость стены Ke для l-8-гo этажей определяется по формуле (18), где ![]() - суммарный
коэффициент податливости стены на длине секции; сi - коэффициент податливости i-го
участка вычисляется по формуле
(17).
- суммарный
коэффициент податливости стены на длине секции; сi - коэффициент податливости i-го
участка вычисляется по формуле
(17).
Для определения коэффициента ![]() стена по длине секции
разбивается на 7 повторяющихся участков (черт. 11) длиной l1=l4=l5= 54см; l2=240 см; l3=160 см; l6=141 см; l7=99 см.
Число участков ni на длине секции равно: n1=14; n2=n4=n5=n6=n7=2; n3=5.
стена по длине секции
разбивается на 7 повторяющихся участков (черт. 11) длиной l1=l4=l5= 54см; l2=240 см; l3=160 см; l6=141 см; l7=99 см.
Число участков ni на длине секции равно: n1=14; n2=n4=n5=n6=n7=2; n3=5.
Расчетная высота кладки hk каждого участка определяется построением зон влияния продольных сил в
соответствии с указаниями п. 12.
Расчетные значения hk каждого участка равны (см. черт.):
Черт. 11. К расчету продольной жесткости межоконного пояса наружной стены
h1=202 см; h2=h3=h7=110 см; h4=184 см; h5=96 см; h6=60 см.
Суммарный коэффициент
податливости Sсi
вычисляется с использованием формул (15) и (17), принимая dk=55 см; Еk=1500
МПа; As=4,52 см2; Es=2×105 МПа; ys=0,7:

2. По формуле (18) средняя
продольная жесткость стены
![]() Па×м2.
Па×м2.
Перекрытия
1. Средняя продольная
жесткость перекрытий Кр определяется по формуле (18), где ![]() суммарный коэффициент
податливости на длине секции, равный
суммарный коэффициент
податливости на длине секции, равный
![]()
где ![]() - суммарный
коэффициент податливости плит перекрытий вычисляется с использованием формул (14) и (17), принимая в них для
плит длиной l=590 см As=65,2 см2; для
плит длиной l=240 см, As=18,6 см2;
- суммарный
коэффициент податливости плит перекрытий вычисляется с использованием формул (14) и (17), принимая в них для
плит длиной l=590 см As=65,2 см2; для
плит длиной l=240 см, As=18,6 см2;
 ;
;
![]() - суммарный
коэффициент податливости кладки поперечных стен (черт. 12) вычисляется по формулам (17) и (11), которые после
преобразования имеют вид:
- суммарный
коэффициент податливости кладки поперечных стен (черт. 12) вычисляется по формулам (17) и (11), которые после
преобразования имеют вид:
![]()
где dp=Bp - расчетная ширина
перекрытия за вычетом проемов и отверстий в стене;
hk - расчетная высота кладки стены, вовлекаемая в совместную работу с
перекрытиями, определяется построением (см. черт. 12).
Полагая в формуле расчета
поперечных стен:
по осям 8,9: ni=2; dk=38 см; а=10 см;
hk=20 см; dp=14 см;
"
" 6,11: ni=1; dk=51 см; а=15 см;
hk=20 см; dp=13 см;
"
" 7,10: ni=2; dk=64 см; а=12 см;
hk=40 см; dp=10,5 см;
получим:
![]()
Черт. 12. К расчету кладка поперечных стен в местах заделки плит перекрытий
2. По формуле (18) средняя
продольная жесткость перекрытий
![]() Па×м2.
Па×м2.
3. По формуле (19) средняя
продольная жесткость сечения этажа
К=(10,76×2+24,5)×108=46,02×108 Па×м2.
ТЕМПЕРАТУРНЫЕ УСИЛИЯ,
НАПРЯЖЕНИЯ И
РАСКРЫТИЕ ТРЕЩИН В КЛАДКЕ СТЕН И ПЕРЕКРЫТИЙ
Здание с регулярной
конструктивной схемой.
В соответствии с указаниями
п. 22 Н0=27,4+2,1=29,5 м; L/H0=108,8/29,5=3,68»3,5.
Относительная высота
положения перекрытий над полом подвала равна: перекрытие над подвалом y0/Н0=2,1/29,5=0,07;
перекрытие над первым этажом y0/Н0=4,9/29,1=0,19;
над вторым - 7,7/29,5=0,27 (см. черт.
10) и т. д.
В качестве примера определяем
усилия, напряжения и раскрытие трещин в кладке наружных и внутренних стен и
перекрытий в двух наиболее напряженных точках, расположенных в уровне
перекрытия над первым этажом y1/H0=0,19; для перекрытий в
середине здания - x/L=0; для наружных стен - в
точке x/L=0,1 (ослабление стены дверным проемом).
Соответствующие значения
коэффициентов nm для этих точек по табл. 4 для L/H0=3,5 y1/H0=0,19 соответственно равны
0,82 и 0,81.
Для других точек стен и
перекрытий расчет выполняется аналогичным образом.
Наружная стена
Суммарное продольное усилие в
кладке и перемычке межоконного пояса стены в точке x/L=0,1 по формуле (46) при nm=0,81:
Kf=0; Ke=10,76×108 Па×м2;
Кр=24,5×108 Па×м2; К=46,02×108 Па×м2;
Dte=-17°С; Dte=-23°С;
Ne=0,81×0,5×10-5×10,76×108(-17)+15,62=-58,46 кН,
где по формуле (49)
![]() кН.
кН.
По формуле (59) продольное
усилие в поясе кладки Nk и перемычки Nr при Кk=9,07×108 Па×м2; Кr=1,3×108 Па×м2 соответственно
равны:
![]() кН;
кН;
![]() кН.
кН.
По формуле (68) напряжение в
кладке по концам перемычки при Nr=-12,16 кН; dk=dr=55 см; dk=60 см; bm=65 см ; am=12 см; Еk=1500 МПа; Dq=50°С (без учета знака Nr) равно

где по формуле (29)
Br,y=54,12×105 Па×м4;
по формуле (21)
![]() Па×м4,
Па×м4,
т. е. в кладке образуются
трещины.
4. По формуле (75) раскрытие
трещин в кладке снаружи по концам перемычек при lm=348 см; lr=240 см; a=0,56×10-5 (1/°С) равно (без учета знака Dt)
![]() мм<[1 мм],
мм<[1 мм],
где по формуле (50)
![]() (1/°С).
(1/°С).
Раскрытие трещин меньше
допустимого. Армирование кладки не требуется.
Перекрытия помещений
Продольные
усилия в плитах перекрытия в месте опирания их на поперечную стену по оси 9
(x/L=0,1) определяется по формуле
(48)
Np=0,81×10-5×24,5×108(-23)-2×15,62=-478,36 кН,
где по формуле (49) DNm=15,62 кН.
Максимальное растягивающее
напряжение в кладке по концам плит перекрытий, заделанных в стену, по формуле (68) при dk=Bp=13 м. Dq=0;
bm=19 см; am=10 см равно
![]() МПа>0,4 МПа.
МПа>0,4 МПа.
В кладке опор образуются
трещины.
Максимальное раскрытие трещин
на опорах по формуле (75) при lm=615 см; l=590 см
равно
de=(-23+0)[0,5×10-5(615-590)+10-5×590]=-1,38 мм<-[0,5+10-5×590×18£1,5 мм],
что удовлетворяет требованиям
табл. 1.
Армирование кладки не
требуется.
Перекрытия лоджий.
Неармированная кладка опор
1. Суммарное усилие в плитах
перекрытий в середине здания (x/L=0, ось 11) по формуле (48); при nm=0,82; Dtp=-23°С; Кр=24,5×108 Па×м2
Np=0,82×10-5×24,5×108(-23)-2×14,80=-482,24 кН,
где по формуле (49) DNm=14,80 кН.
2. Усилия в плитах лоджий Np,b при Dtp,b=-42°С, ширине Bp,b=2
м; Kp,b=3,7×108 Па×м2 вычисляются по формуле (60):

3. Максимальные растягивающие
напряжения в кладке опор плит лоджий на стену по оси 11 вычисляются по формуле (68) при bm=25,5 см; am=15 см; Dq=0
![]() МПа>Rtu=0,4
МПа.
МПа>Rtu=0,4
МПа.
В кладке образуются трещины.
4. Максимальное раскрытие
трещин на опорах по формуле (75) при lm=615 см; l=590 см;
Dtp,b=-42°С
![]() мм>[1,5мм],
мм>[1,5мм],
что не удовлетворяет
требованиям табл. 1.
Кладку опор следует
армировать.
АРМИРОВАННАЯ КЛАДКА ОПОР
Требуемое количество арматуры
класса A-III (Rs=360 МПа) для армирования
кладки опор перекрытий определяется методом последовательного приближения.
Первое приближение
A¢s=Np,b/Rs=130200/360×106=3,6×10-4 м2=3,6
см2.
Коэффициенты упругой
податливости кладки левой и правой опор по формулам (14), (17):
![]() м/(Па×м2);
м/(Па×м2);
то же, плит перекрытий l=590 см;
Аs=2×4=8 см2:
![]() м/(Па×м2).
м/(Па×м2).
По формуле (18)
![]() Па×м2.
Па×м2.
По формуле (60)
![]() кН.
кН.
Второе приближение
Fs"=-75120/360×106=2,09 см2;
![]() м/(Па×м2);
м/(Па×м2);
![]() Па×м2.
Па×м2.
![]() кН,
кН,
что близко предыдущему
результату.
По формуле (76) максимальное
раскрытие трещин в армированной кладке по оси 11 при Dq=0:
![]()
что удовлетворяет требованиям
табл. 1.
НАРУЖНЫЕ СТЕНЫ ЛЕСТНИЧНЫХ
КЛЕТОК
Расчетная схема стен и
перекрытий средней лестничной клетки между осями 8 и 9 показана на черт. 13.
Расчетные усилия в наружной
стене и перекрытии первого этажа в точке x/L=0,1 (см. выше):
Nе=-58,46 кН; Nр=-478,36 кН.
Расчетное усилие в одной
плите шириной 1,2 м при расчетной ширине перекрытия Вр=13 м равно
![]() кН.
кН.
По формуле (63) расчетное
усилие в наружной стене лестничной клетки равно
![]() кН,
кН,
в том числе в поясе кладки Nk(B) и в перемычке Nr(B)
по формуле (59) при Kk=9,07×108 Па×м2 и Kr=1,3×108 Па×м2
![]() кН;
кН;
![]() кН.
кН.
Растягивающие напряжения в
поясе кладки по формуле (67)
при Аk=110×55=6050 см2; Dq=50°С
![]() .
.
Черт. 13. Расчетная схема лестничной клетки
Трещины не возникнут.
То же, по концам перемычки
по формуле (68) при Nr(B)=-17,97 кН; Nr=12,16 кН (см. выше); bm=64 см; am=12 см; Br,y=54,12×105 Па×м4; Bk=124,8×105 Па×м4:

Возникнут трещины.
Максимальное раскрытие
трещин по концам перемычки по формуле
(75) при lm=260 см; lr=160 см

что удовлетворяет
требованиям табл. 1. Армирование
кладки не требуется.
Пример 2. Определить температурные
усилия в стенах и перекрытии одноэтажного промышленного здания пролетом l=18 м и
высотой h=3,9 м (до низа железобетонных балок), показанного
на черт. 14, при расчете
изменения температуры Dt=50°С.
Стены кирпичные с пилястрами
из глиняного кирпича марки 75 и раствора марки 75. Перекрытие из сборных
железобетонных плит по предварительно напряженным железобетонным балкам
пролетом 18 м.
Черт. 14. К расчету
температурных усилий в стенах и перекрытии одноэтажного промышленного здания
а, б - разрез и план; в -
расчетная схема рамы
Здание в поперечнике
представляет раму (один раз статически неопределимую), стойки которой имеют
разную изгибную жесткость (черт. 14.
в). Изгибная жесткость стойки АВ на длине h1=315 см, B1=14,9×107 Па×м4; на длине h2=75 см, B2=6×107 Па×м4; стойки CD-h=390
см, B3=9,1×107 Па×м4.
Коэффициент упругой
податливости балки cр=5,27×10-9 м/(Па×м2), коэффициент
температурного расширения a=10-5 (1/°С).
При решении задачи методом
сил за неизвестное принимаем усилие в ригеле (балке), которое находится из уравнения (43):
d11X+D1t=0,
откуда X=-D1t/d11.
Коэффициент d11
вычисляется по формуле (44)
с учетом упругой податливости ригеля (начало координат вверху стоек):
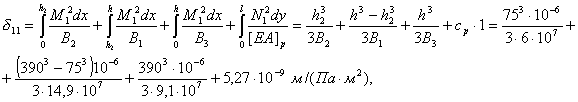
где М1=lx; cp=l/[EA]p.
Коэффициент Dit находится по формуле (45):
 м=9 мм.
м=9 мм.
Подставляя в формулу метода
сил найденные значения коэффициентов, получим усилие в ригеле
![]() кН
кН
(при жестком ригеле ср=0,
Np=25,6 кН).
Изгибающие моменты внизу
стоек (сечения I-I и III-III)
MA=MD=Nph=25,2×3,9=98,4 кН×м,
то же, в сечении II-II
Mc=Nph2=25,2×0,75=18,9 кН×м.
Перемещения (прогибы) стоек
вверху:
стойка АВ
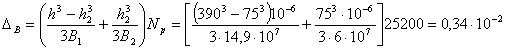 м=3,4 мм;
м=3,4 мм;
стойка CD
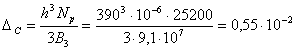 м=5,5 мм.
м=5,5 мм.
Удлинение ригеля Dр=9-(3,4+5,5)=0,1
мм.
ПРИЛОЖЕНИЕ 12
ОСНОВНЫЕ БУКВЕННЫЕ ОБОЗНАЧЕНИЯ
ПРОПИСНЫЕ БУКВЫ ЛАТИНСКОГО
АЛФАВИТА
As - площадь сечения арматуры;
Ak - площадь сечения кладки;
А - расчетная площадь
сечения элемента;
площадь сечения полки
(участка продольной стены, учитываемого в расчете);
поперечное сечение
перемычки;
суммарная площадь сечения
кладки и железобетонных элементов в опорном узле в пределах контура стены или
столба, на которые уложены элементы;
Ac - площадь сжатой части сечения при прямоугольной эпюре
напряжений; площадь смятия, на которую
передается нагрузка;
Аn
- расчетная площадь сечения нетто:
площадь нетто
горизонтального сечения стены;
площадь горизонтального сечения настила, ослабленная пустотами, на длине опирания настила на кладку (суммарная площадь сечения ребер);
Ared - площадь приведенного сечения;
Ac,red - площадь сжатой части приведенного сечения;
Ast - сечение арматуры;
Ab - площадь брутто горизонтального сечения стены;
суммарная площадь опирания
железобетонных элементов в узле;
Е0 - модуль
упругости (начальный модуль деформаций) кладки;
Е – модуль деформаций кладки;
Еb – начальный модуль упругости бетона;
Еs – модуль упругости стены;
G – модуль сдвига кладки;
H – расстояние
между перекрытиями или другими горизонтальными опорами;
высота этажа;
H1 – высота верхнего участка стены;
расстояние над верхней гранью рандбалки;
H2 – высота эквивалентного по жесткости рандбалке условного пояса кладки;
I –
момент инерции сечения стен относительно оси, проходящей через центр тяжести
сечения стен в плане;
Is – момент инерции сечения стальной рандбалки;
L –
размер сечения элементов при расчете на смятие соответственно схемам черт. 9;
M – расчетный
изгибающий момент;
наибольший изгибающий момент
от расчетных нагрузок;
момент от нормативных
нагрузок, который будет приложен после нанесения на поверхность кладки
штукатурных или плиточных покрытий;
изгибающий момент от
расчетных нагрузок в уровне перекрытия или покрытия в местах опирания их на
стену на ширине, равной расстоянию между анкерами;
N –
расчетная продольная сила;
расчетная осевая сила при
растяжении;
продольная сила от
нормативных нагрузок, которая будет приложена после нанесения на поверхность
кладки штукатурных или плиточных покрытий;
расчетная нормальная сила в
уровне расположения анкера на ширине, равной расстоянию между анкерами;
опорная реакция рандбалки он
нагрузок, расположенных в пределах ее пролета и длины опоры, за вычетом собственного
веса рандбалки;
Ng – расчетная продольная сила от длительных нагрузок;
Nc – продольная сжимающая сила от местных нагрузок;
Ncc – расчетная несущая способность;
Ns – расчетное усилие в анкере;
Q –
расчетная поперечная сила;
расчетная поперечная сила от
горизонтальной нагрузки в середине высоты этажа;
расчетная поперечная сила от
горизонтальной нагрузки, воспринимаемая поперечной стеной в уровне перекрытия,
примыкающего к рассматриваемым перемычкам;
расчетная нагрузка от веса
балки и приложенных к ней нагрузок;
R –
расчетные сопротивления сжатию кладки;
Rk – расчетные сопротивления сжатию виброкирпичной кладки на тяжелых
растворах;
Rtb – расчетное сопротивление растяжению при изгибе кладки;
Rtw – расчетное сопротивление кладки главным растягивающим напряжениям;
Rsq – расчетные сопротивления при срезе кладки;
Rs – расчетные сопротивления арматуры;
Ru – временное сопротивление (средний предел прочности) сжатию кладки;
Rsku – временное сопротивление (средний предел прочности) сжатию
армированной кладки из кирпича или камней;
Rsn – нормативное сопротивление арматуры в армированной кладке;
Rc – расчетное сопротивление кладки при смятии;
Ri – расчетное сопротивление любого другого слоя стены;
Rsk – расчетное сопротивление кладки с сетчатым армированием при осевом,
центральном сжатии;
RI – расчетное сопротивление сжатию неармированной кладки в
рассматриваемый срок твердения раствора;
R25 – расчетное сопротивление
кладки при марке раствора 25;
Rskb – расчетное сопротивление армированной кладки при внецентренном сжатии;
Rstq - расчетное сопротивление скалыванию кладки, армированной продольной
арматурой в горизонтальных швах;
Rb – расчетное сопротивление бетона осевому сжатию;
S0 – статический момент части
сечения, находящейся по одну сторону от оси, проходящей через центр тяжести
сечения;
S – длина
участка эпюры распределения давления в каждую сторону от грани опоры;
S1 – длина участка
распределения треугольной эпюры давления над крайними опорами рандбалок, а
также над опорами однопролетных рандбалок от грани опоры;
T –
сдвигающее усилие в пределах одного этажа;
перерезывающие усилия в
перемычках;
Vs – объем арматуры;
Vk – объем кладки;
W –
момент сопротивления сечения кладки при упругой ее работе.
СТРОЧНЫЕ БУКВЫ ЛАТИНСКОГО
АЛФАВИТА
a, b, c, c1, h – геометрические размеры
сечения элементов при расчете на смятие в соответствии со схемами черт. 9;
a –
глубина заделки балки в кладку;
длина опоры (ширина
простенка);
a1 – длина опорного участка
рандбалки;
b –
ширина сжатой полки или толщина стенки таврового сечения в зависимости от
направления эксцентриситета;
фактическая ширина слоя при
расчете многослойных стен;
ширина сечения элемента;
ширина полок балки;
bc – ширина балки;
bred – приведенная ширина слоя;
c –
размер квадратной ячейки сетки;
расстояние то точки
приложения силы Q до плоскости стены;
cb, ch – расстояние то точки приложения силы Q до
ближайших границ прямоугольного сечения элемента;
e0 – эксцентриситет действия
расчетной нагрузки;
эксцентриситет расчетной силы
относительно середины заделки;
e0g –
эксцентриситет действия длительных нагрузок;
eb, eh – эксцентриситеты при косом внецентренном сжатии
прямоугольного сечения элемента соответственно сторонам;
g –
коэффициент, зависящий от величины площади опирания железобетонных элементов в
узле;
h –
меньший размер прямоугольного сечения;
меньшая сторона
прямоугольного сечения столба;
толщина стены;
высота сечения;
толщина поперечной стены;
высота перемычки в свету;
hc1, hc2 –
высоты сжатой части элементов в сечениях с максимальными изгибающими моментами;
hred – условная толщина стен, столбов сложного сечения;
h0 – расстояние от сжатого края
сечения стены до оси анкера (расчетная высота сечения);
hc – высота сжатой части поперечного сечения Ас в плоскости
действия изгибающего момента;
i –
наименьший радиус инерции сечения элемента;
радиус инерции стен, столбов
сложного сечения;
ic – радиус инерции сжатой части поперечного сечения Ас в
плоскости действия изгибающего момента;
ib, ih – радиусы инерции при косом внецентренном сжатии
прямоугольного сечения элемента соответственно сторонам;
ic1, ic2 –
радиусы инерции сжатой части элементов в сечениях с максимальными изгибающими
моментами;
k –
коэффициент, принимаемый по табл. 14;
поправочные коэффициенты;
kp – коэффициент для столбов;
l0 – расчетная высота (длина)
стен и столбов;
l01 – расчетная высота верхнего
участка стены;
l – длина
поперечной стены в плане;
пролет перемычки в свету;
свободная длина стены;
lc – основание треугольной эпюры распределения над крайними опорами
рандбалок, а также над опорами однопролетных рандбалок;
m –
коэффициент использования прочности слоя, к которому приводится сечение при
расчете многослойной стены;
mg – коэффициент, учитывающий влияние длительного воздействия нагрузки;
mi – коэффициент использования прочности любого другого слоя стены;
n –
эмпирический коэффициент, используемый при расчете на срез;
p –
коэффициент, зависящий от типа пустот в железобетонном элементе;
s –
расстояние между сетками по высоте;
v -
коэффициент неравномерности касательных напряжений в сечении;
у - расстояние от центра
тяжести сечения элемента в сторону эксцентриситета до сжатого его края;
расстояние от оси продольной
стены до оси, проходящей через центр тяжести сечения стен в плане;
yb, yh - расстояния от центра тяжести элемента
прямоугольного сечения до его края в сторону эксцентриситета, соответственно
сторонам, при косом внецентренном сжатии;
z - плечо
внутренней пары сил.
СТРОЧНЫЕ БУКВЫ ГРЕЧЕСКОГО
АЛФАВИТА
a - упругая характеристика
кладки;
ared
- приведенная упругая характеристика кладки;
ask
- упругая характеристика кладки с сетчатым армированием;
at -
коэффициент линейного расширения кладки;
a1, a2 - упругие характеристики
слоев кладки в многослойной стене и соответственно их толщины;
b
- отношение высоты этажа к толщине стены или меньшей стороне прямоугольного
сечения столба;
gс -
коэффициент условий работы кладки;
gс1
- коэффициент условий работы для зимней кладки;
коэффициент условий работы
кладки в стадии оттаивания;
gсs - коэффициент условий работы арматуры;
g
- плотность;
gr - коэффициент условий работы
кладки при расчете по раскрытию трещин;
gсs1 - коэффициент условий работы сетчатой арматуры при
расчете кладки в стадии оттаивания;
є - относительная деформация
кладки;
єu -
предельная относительная деформация;
h - коэффициент, принимаемый
по табл.20;
lh, li -
гибкость элементов соответственно прямоугольного сечения и сечения произвольной
формы;
lh1c, lh2c -
гибкости сжатой части элементов в сечениях с максимальными изгибающими
моментами;
m - процент армирования
сетчатой арматурой кладки по объему;
процент армирования по
вертикальному сечению стены;
коэффициент трения;
n
- коэффициент, учитывающий влияние ползучести кладки;
x1 -
коэффициент, зависящий от материала кладки и места приложения нагрузки,
определяется по табл. 21;
s
- напряжение в кладке, при котором определяется є;
s0 -
среднее напряжение сжатия при наименьшей расчетной нагрузке, определяемой с
коэффициентом перегрузки 0,9;
sc - максимальное напряжение
над опорой рандбалки;
j
- коэффициент продольного изгиба;
jc - коэффициент продольного
изгиба сжатой части сечения элемента;
j1 -
коэффициент продольного изгиба при внецентренном сжатии элемента;
y
- коэффициент полноты эпюры давления от местной нагрузки;
w - коэффициент, принимаемый
по табл.19.
СОДЕРЖАНИЕ
|
|
|
|


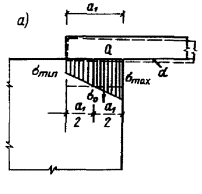









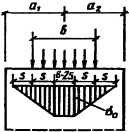

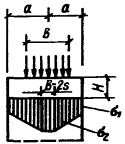

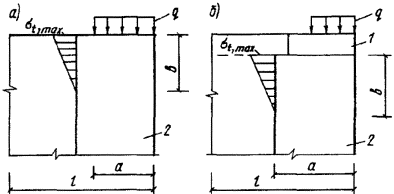




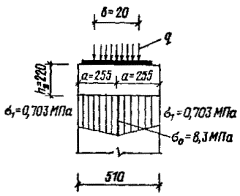
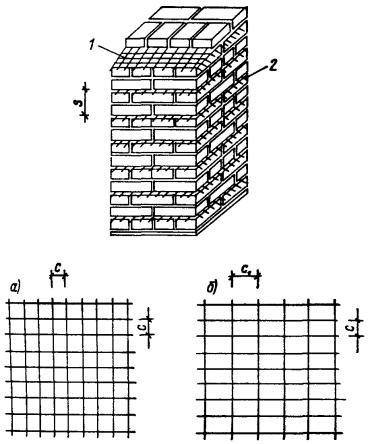


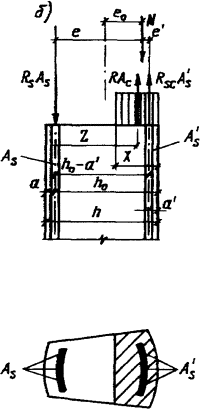





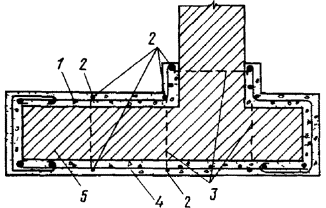
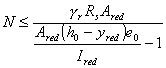



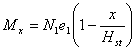 ;
;
 ;
;