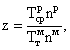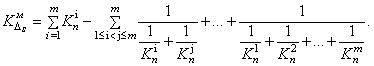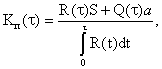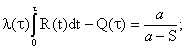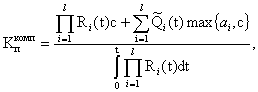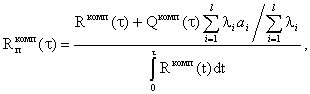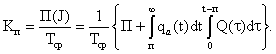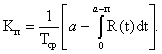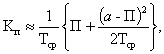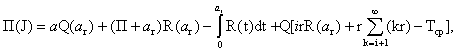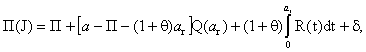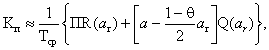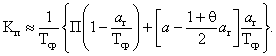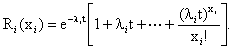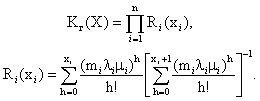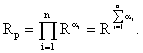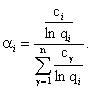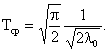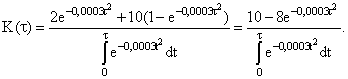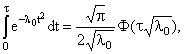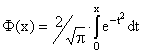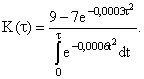|
|
МИНИСТЕРСТВО
ТРАНСПОРТНОГО СТРОИТЕЛЬСТВА ВСЕСОЮЗНЫЙ ОРДЕНА
ОКТЯБРЬСКОЙ РЕВОЛЮЦИИ УТВЕРЖДАЮ Зам. директора института Г.Д. ХАСХАЧИХ «18» декабря 1984 г. МЕТОДИЧЕСКИЕ
РЕКОМЕНДАЦИИ Одобрены
Главтоннельметростроем Москва 1985 ПРЕДИСЛОВИЕ
В настоящей
работе изложены методика расчета надежности системы тоннельного оборудования в
зависимости от выбранной технологической схемы, способы повышения и оптимизации
надежностных показателей с целью ускорения проходки и повышения
производительности применяемых машин и механизмов, а также приведены
приближенные формулы, не требующие использования ЭВМ. Для облегчения
практического применения Методических рекомендаций составлены алгоритмы и
программы, которые находятся в библиотеке исходных модулей ЕС ЭВМ, ЦНИИСа и
сданы в ГосФАП. При разработке
Методических рекомендаций использованы результаты научно-исследовательских
работ ЦНИИСа, проведенных совместно с Бамтоннельстроем и МИСИ им. В.В.
Куйбышева, хронометражных наблюдений и анализа работы оборудования на объектах
Бамтоннельстроя, Армтоннельстроя и Тбилтоннельстроя, а также справочный
материал. Методические рекомендации
предназначены для проектных, конструкторских, строительных и
научно-исследовательских организаций, занимающихся вопросами создания новой
техники, формирования и эксплуатации горно-проходческих комплексов при
сооружении транспортных тоннелей. Рекомендации
подготовили канд. физ.-мат. наук И.З. Маневич, кандидаты техн. наук Л.С.
Афендиков, В.Е. Меркин, (ЦНИИС), д-р физ.-мат. наук А.Л. Гаркави (МИСИ), инж.
В.З. Коган (Бамтоннельстрой) при участии инженеров В.В. Сороки, М.Б.
Евдокимовой, О.Г. Шостаковской (ЦНИИС). Замечания и
предложения просим присылать по адресу: 129329, Москва, ул. Кольская, 1, ЦНИИС. Зав.
отделением тоннелей и метрополитенов
Л.С. Афендиков 1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Согласно
ГОСТ 13377-75 «надежность - свойство объекта выполнять заданные функции,
сохраняя во времени значения установленных эксплуатационных показателей в
заданных пределах...». В настоящей работе рассматривается надежность
горно-проходческого комплекса, выполняющего работу на основе выбранной
технологической схемы. Каждая технология, определяя различные способы работы
оборудования (параллельные, последовательные, комбинированные), различные
методы организации работы (непрерывные или с технологическими перерывами)
влияет на скорость проходки, время простоя машин и механизмов и другие
параметры, обусловливающие производительность комплекса. Поэтому
надежность выбранного комплекса машин и механизмов, функционирующих на основе
данной технологической схемы, следует определять термином технологическая надежность. 1.2. При строительстве
транспортных тоннелей необходимо так организовать технологический процесс,
чтобы улучшить или даже оптимизировать его надежностные показатели с целью
ускорения проходки, повышения эксплуатационной производительности машин и
оборудования. Применение целых комплексов функционально связанных механизмов с
различными эксплуатационными режимами требует эффективного сочетания
механизмов, рационального построения технологических цепочек и циклов,
характеризуемых количеством и последовательностью выполнения производственных
операций. Оптимальные режимы эксплуатации и обслуживания существенно воздействуют на
повышение надежности, производительности и экономической эффективности
комплекса в целом. Ввиду многообразия возможных вариантов выбор наилучшего решения
не является простой задачей и требует комплексного применения инженерных и
математических методов. 1.3. В качестве
показателя технологической надежности принимается коэффициент простоя Кп,
равный отношению времени простоя tпр машины к ее
наработке tраб за большой
период эксплуатации при выбранной технологической схеме:
Коэффициент
простоя связан с коэффициентом готовности соотношением
К времени
простоя tпр следует
относить только время аварийных и профилактических ремонтов (не считая времени
простоя по организационно-техническим причинам и простоев, предусмотренных
технологией производства работ), полагая, что в результате каждого ремонта
механизм полностью восстанавливает свою работоспособность. 1.4. Для оценки
технологической надежности и разработки рекомендаций по ее повышению проводятся
хронометражные наблюдения за работой горно-проходческого комплекса в ряде
выбранных забоев. Форма журнала
хронометражных наблюдений приведена в приложении 1. 2. РАСЧЕТ КОМПЛЕКСНОГО ПОКАЗАТЕЛЯ ДЛЯ ОЦЕНКИ УРОВНЯ
ТЕХНОЛОГИЧЕСКОЙ СХЕМЫ
2.1. Для
количественной оценки уровня технологической схемы и выбора лучшей из ряда
возможных для данных горно-геологических условий вводится комплексный
показатель - величина полезной производительности труда за цикл где V - заданный объем работ на одном цикле, в единицах работы ведущего
механизма: объем грунта, метры проходки и т.д.; a - коэффициент приближения сечения
выработки S к площади S′, необходимой для пропуска транспорта; n - численность рабочего персонала; Тср -
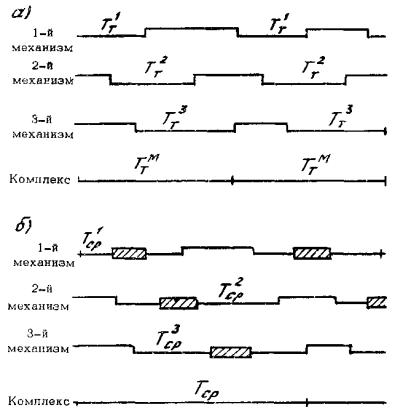
средняя длительность цикла с учетом простоев и технологических перерывов (рис. 1, б). 2.2. Для учета
степени механизации технологического процесса вводится коэффициент,
характеризующий долю ручного труда p относительно
механизированного M:
где Ттм - теоретическое,
определяемое по циклограмме время работы механизмов (см. рис. 1, а); Тсрр
- среднее время работ, выполняемых вручную; nр и nм - число рабочих
и машин. Тогда формула (1) примет вид
где 2.3. Для определения
коэффициента простоя механизмов Kпм необходимо
вычислить значения Тт в соответствии с циклограммой работ, а также
время и коэффициент простоя каждого механизма на цикле Тпi
Рис. 1. Схемы
расчета Ттм и Тср для системы механизмов:
Для вычисления Кпм
надо разбить цикл на промежутки {DS}S = 1, 2,…N, на каждом из которых
работает постоянное число m одних и тех же механизмов (рис. 2). Рис. 2. Схема
разбиения цикла на интервалы для расчета коэффициента простоя
горно-проходческого оборудования. Обозначения см. на рис. 1 Тогда где а каждый KDs вычисляется по
формуле
2.4. Уровень технологической схемы рекомендуется
оценивать отношением
где ут - комплексный показатель
для оценки уровня технологической схемы; п -
производительность труда по исследуемой технологической схеме; пб -
производительность труда по базовой технологии. В качестве
базовой может быть принята, например, как эталон поточная технология для механизированного
сооружения тоннелей машинами роторного типа с непрерывным креплением выработки
и уборкой грунта в процессе его разработки. Пример расчета ут
дан в приложении 2. 3. ОПТИМИЗАЦИЯ ПЕРИОДА ДЛИТЕЛЬНЫХ ПРОФИЛАКТИЧЕСКИХ РЕМОНТОВ
3.1. Одним из
методов повышения технологической надежности является профилактический ремонт
машин и механизмов. Циклический характер позволяет приурочить его полностью или
частично к периодам технологических перерывов в работе механизма1. 1В дальнейшем рассматриваются
только длительные профилактические ремонты, время которых больше времени
технологических перерывов. Профилактический
ремонт позволяет уменьшить количество и длительность аварийных ремонтов, а
следовательно, и простои оборудования. Однако длительный профилактический
ремонт сам ведет к простою механизма и снижению его производительности.
Существующие нормативные документы по проведению профилактических ремонтов не
учитывают
ни надежности машин, ни принятой технологической схемы. В настоящих
Методических рекомендациях дается оценка технологической надежности в
зависимости от частоты и длительности профилактических ремонтов и определения
оптимального периода профилактики (пп. 3.2
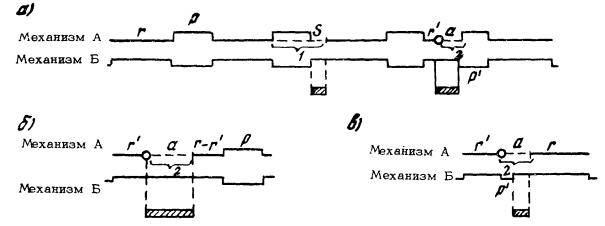
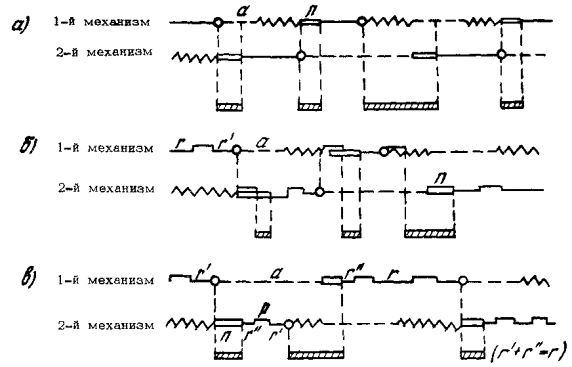
- 3.5). 3.2. На рис. 3, а приведена схема комплекса оборудования, состоящего из
ведущего механизма А и вспомогательного механизма Б, работающих в такой последовательности.
Во время аварийного ремонта механизма А механизм Б простаивает; по окончании
ремонта начинает действовать механизм Б, который работает неполный период и
выполняет объем работ, подготовленный механизмом А до его ремонта. После
завершения работы механизмом Б начинает снова работать механизм А. Коэффициент
простоя на промежутке (0,t) выражается по
формуле где Q(t) - функция распределения случайного времени исправной работы
механизма А на данном промежутке; R(t) - функция
надежности; a - длительность аварийного ремонта;
Здесь р - время технологического
перерыва механизма А (или рабочий период механизма Б). Время t принимается
кратным r - рабочему периоду механизма А t = mr (m = 0, 1, 2,…). Из формулы (7) определяется число полных рабочих
периодов m*, после которых необходим
профилактический ремонт, чтобы коэффициент простоя был минимальным, m* = [t*/r], где t* находится как
корень уравнения
Рис. 3. Схема
расчета коэффициента простоя системы машин и механизмов для различных
технологических схем: 1 - профилактический ремонт; 2 - аварийный; Функция Q(t) определяется из
опыта путем наблюдений за работой машины. Обычно опасность отказов l(t) является неубывающей функцией, исключая лишь начальный период
эксплуатации машины (период приработки, когда обнаруживаются скрытые дефекты
изготовления). Поэтому в качестве Q(t) принимается закон Вейбулла
для которого l0 = p/2×1/2Tср2, Тср - среднее время
безотказной работы машины. В соответствии с
изложенной методикой расчет оптимального периода профилактики может быть
проведен по специально составленной программе T1SPR1 для машин серии ЕС ЭВМ. Расчет оптимального
периода профилактических ремонтов для данной схемы приведен в приложении 3 (пример 1). 3.3. Для схемы, представленной на рис. 3, б, возможна
ситуация, когда во время аварийного ремонта механизма А механизм Б также
простаивает. Но после окончания ремонта сначала вновь включается механизм А,
который должен работать столько времени, чтобы его суммарное время работы до
аварийного ремонта r¢ и после него Расчет
оптимального периода профилактики для указанной схемы организации работ дан в
приложении 3 (пример 2). 3.4. Если во время аварийного ремонта механизма А механизм Б
работает и выполняет объем работ, подготовленный ведущим механизмом до
аварийного ремонта (см. рис. 3, в), то потери времени при эксплуатации комплекса равны a - qr¢ при a > qr¢. Тогда
коэффициент простоя
Отсюда, используя
программу T1SPR2, можно найти оптимальный период профилактики m*, при котором Kп(mr) = min. Следует отметить,
что Kп(mr) - функция, имеющая несколько минимумов; однако, задав степень
точности e, можно найти
требуемый минимум. Расчет
оптимального периода профилактики при совмещенном способе производства работ
дан в приложении 3 (пример 3). 3.5. Если горно-проходческий комплекс состоит из l механизмов, подверженных отказам в период их работы, то
коэффициент простоя комплекса Kпкомп выразится через
коэффициенты простоя отдельных механизмов Kпi: в случае
последовательной работы механизмов где qi = ri/pi (ri - время работы i-го механизма на
цикле; pi - время
технологического перерыва i-го механизма на
цикле); в случае
одновременной работы механизмов
где ai - продолжительность аварийного ремонта
механизма Ai; Оптимизация
коэффициента простоя в случае последовательной работы комплекса производится по
каждому механизму в отдельности (см. п. 3.2). При
одновременной работе нескольких механизмов формула (11) даст для этого варианта оценку сверху. Расчет
оптимального периода профилактики при l механизмах в горно-проходческом комплексе дан в приложении 3 (пример 4). В случае
распределения Вейбулла
где В общем случае
вероятности 4. ПОВЫШЕНИЕ
ТЕХНОЛОГИЧЕСКОЙ НАДЕЖНОСТИ МЕТОДОМ РЕЗЕРВИРОВАНИЯ МАШИН
4.1.
Резервирование горно-проходческих машин и механизмов для транспортного
строительства является эффективным методом повышения технологической надежности
и производительности труда в строительстве. Наиболее распространенный
случай резервирования - дублированная система, состоящая из двух идентичных
восстанавливаемых механизмов. Важным показателем надежности такой системы
является коэффициент простоя. Здесь возможны три варианта (рис. 4): Рис. 4. Схема
расчета коэффициента простоя оборудования при дублировании механизмов:
а)
Технологические перерывы отсутствуют (р = 0) и включенный механизм работает
непрерывно до момента его отказа (см. рис. 4, а). Процесс
функционирования системы, начиная с 1-го отказа механизма, распадается на
статистически однородные интервалы, заключенные между двумя последовательными
моментами включения механизмов, находившихся в резерве. Каждый такой интервал J включает период исправного функционирования системы и
период ее простоя. Поскольку при t ® ¥ число таких интервалов с вероятностью 1 неограниченно
растет, то отношение суммарного времени простоя к суммарному времени работы
системы сходится по вероятности к П(J)/Т(J), где П(J) -
математическое ожидание времени простоя на интервале J; Т(J) - математическое ожидание времени работы на интервале J. Таким образом, Kп = П(J)/Т(J). Очевидно, что Т(J) = Тср, где Тср - математическое
ожидание времени Т безотказной работы одного механизма. Далее определяется Kп. Можно считать, что t = 0 является началом интервала J. Пусть Q(t) и q(t) - функция и плотность распределения времени безотказной
работы механизма, R(t) = 1 - Q(t) - функция надежности механизма, П(t) - математическое ожидание времени простоя системы на J при условии отказа в момент t механизма, включенного при t = 0. Если a - случайная
величина (a > П) с плотностью
распределения qa(t), то
В частности, если
a = const, то При небольших
значениях a можно вместо (15) использовать приближенную формулу
которая получается из (15), если принять Q(t) линейной на [0, а-П]. Если Q(a-П) также
неизвестно, то значение
получаемое в предположении равномерного
распределения Т на [0, Тср]. б) При выходе из
строя работающего механизма технологический перерыв начинается в момент его
отказа и имеет длительность р¢,
пропорциональную предшествовавшему (неполному) рабочему периоду r¢; p¢ = qr¢ (см. рис. 4, б). Этот вариант соответствует, в
частности, случаю, когда продолжение общего технологического процесса не обусловлено
обязательным выполнением всего объема работ, выполняемого данной системой в
течение полного рабочего периода r. Если П > р,
аналогично варианту a имеем где ar - наработка
механизма, включенного при t = 0, на
интервале [0, a-П] без учета соответствующих
перерывов; i - число полных рабочих периодов, содержащихся в интервале
[0, a-П], так что ir £ ar £ (i + 1)r. Приближенное
выражение имеет вид а при неизвестных R(ar), Q(ar)
Для случая П < р выражения (18) и (19)
дают оценку сверху, если принять в них П = р. в) При отказе
механизма технологический перерыв делается лишь тогда, когда наработка системы
после предшествовавшего перерыва станет равной r - полному рабочему периоду (см. рис. 4, в). Пусть br - наработка механизма,
работающего без отказа, за время восстановления другого механизма, т.е. на
интервале [0, a-П]. В этом варианте br случайна, ar -p £ br £ ar. Аналогично
предыдущему
где Приближенное
значение Kп дает соотношение
а при неизвестной R(ar)
Для практических
прогнозов часто достаточно использовать приближенные формулы, поскольку и точные
формулы не могут отразить всей сложности реального технологического процесса в
тоннелестроении. Комплекс
горно-проходческого оборудования рассматривается как сложная система, состоящая
из некоторых подсистем (ряда машин и механизмов), работающих последовательно,
т.е. отказ хотя бы одной из подсистем приводит к отказу всей системы. Тогда
вероятность безотказной работы (надежность) системы
где Ri - вероятность безотказной работы i-й подсистемы. Если машины или
механизмы каждой подсистемы резервировать, то, очевидно, Ri = Ri(xi), где xi ³ 0 - количество
резервных элементов каждой подсистемы, и тогда
где X = x1, x2, … xn - n-мерный вектор. Требуется найти
при условии, что где ci - стоимость единицы резервного оборудования i-й подсистемы; c0 - ограничения на затраты средств. Эта задача решается
методом мажорирующих последовательностей, предложенным Дж. Кеттелем и развитым
Ф. Прошаном и Т. Брейем, являющимся модификацией метода динамического
программирования. При этом принимается, что каждый элемент i-й подсистемы имеет надежность ri, не зависящую от других элементов этой подсистемы. Тогда
В данном методе
строится вначале доминирующая последовательность для системы, состоящей из двух
подсистем. Для этого составляется таблица с двумя входами (значениями х1
и x2), на пересечении которых
указываются c(x1,x2) = c1x1 + c2x2 - стоимость
системы с резервными элементами x1 и x2 и Q(x1,x2) -
ненадежность системы. В таблицу
вносятся лишь такие X, которые удовлетворяют условию (25). Затем, сравнивая c(x1,x2) и Q(x1,x2), стоящие в
таблице, исключают мажорируемые векторы, т.е. такие, для которых в таблице
существует по крайней мере один вектор, все координаты которого не превышают по
величине координат соответствующего мажорируемого им вектора, причем по крайней
мере одна из координат строго меньше. Оставшиеся векторы составляют
мажорирующую последовательность. Затем эта мажорирующая последовательность берется
в качестве первого входа второй матрицы, а в качестве второго входа берется
третья подсистема и описанная процедура повторяется. Таким образом строится
мажорирующая последовательность для системы, содержащей n подсистем. Для уменьшения количества членов мажорирующей
последовательности можно ввести допустимую погрешность e по стоимости и допустимую
погрешность d по ненадежности.
Другим методом сокращения длины мажорирующей последовательности является
использование наибольших начальных значений xi0. Для практических
расчетов по определению оптимального горно-проходческого комплекса составлена
программа T1MRV1 для машин серии ЕС ЭВМ. Программа составлена для не более чем
трех ограничений (25) системы, состоящей
не более чем из 64 подсистем, причем в каждой подсистеме допускается не более
20 машин или механизмов. Длина доминирующей последовательности, образующейся в
процессе вычислений, не должна превышать 1024 числа. Пример расчета
оптимального количества резервных машин дан в приложении 4.
коэффициент простоя для подсистемы,
состоящей из механизма Ai и (ni - 1) резервных,
то
Коэффициент
простоя всей системы и, значит, Kпкомп можно
минимизировать описанным в п. 4.2
методом доминирующих последовательностей. Эта возможность реализована во втором
варианте программы T1MRV1. 4.4. Предложенная
в пп. 4.2 и 4.3 методика может быть применена также для расчетов
оптимального количества резервных запасных частей машин и оборудования. Пусть необходимо,
чтобы машина или оборудование функционировали в течение времени (0, t). В случае отказа какой-либо детали она сразу заменяется из
числа запасных, если таковая есть. Считается, что нехватка запасных деталей
хотя бы одного типа приводит к простою машины, а также, что запасными деталями
машина обеспечивается с момента начала ре работы. Рассматриваются два случая: 1. Запасные детали не ремонтируются. Пусть Ri(xi) - вероятность того, что за время функционирования
системы потребуется не более xi деталей i-го типа (i = 1, 2,…, n), т.е. что в течение времени t произойдет не более xi отказов деталей
(x1, x2, …, xn), то вероятность
бесперебойной работы системы в течение времени t будет Если стоимость
каждой детали i-го типа ci, общие затраты не должны превышать c0, то имеем ограничения Если
предположить затем распределение времени до отказа деталей i-го типа экспоненциальным, тогда
2. Запасные детали ремонтируются. В этом
случае отказавшая деталь заменяется, если это возможно, запасной. Отказавшая деталь
сразу же поступает в ремонт. В машине же непрерывно должно функционировать mi, деталей i-го типа, а в запасе иметься xi деталей того же типа. Каждая из деталей характеризуется
экспоненциальным распределением времени работы до отказа, т.е. Тогда
коэффициент готовности, т.е. вероятность того, что машина не будет простаивать из-за
того, что отсутствует деталь для замены в момент отказа, определяется по
формуле
Как и в случае 1, задача состоит в выборе вектора X, максимизирующего Кг(Х) при наличии линейных
ограничений
Следовательно, и
здесь применимы методика и алгоритмы п. 4.2. 5. ЭКОНОМИЧЕСКАЯ ОЦЕНКА НАДЕЖНОСТИ ГОРНО-ПРОХОДЧЕСКОГО
ОБОРУДОВАНИЯ И ТЕХНОЛОГИЧЕСКИХ СХЕМ СООРУЖЕНИЯ ТРАНСПОРТНЫХ ТОННЕЛЕЙ
5.1.
Экономическую оценку надежности машин следует давать путем исчисления потерь,
возникающих при эксплуатации данной машины в данных условиях из-за ее
ненадежности, В эту оценку должны входить затраты на аварийные ремонты, на
техническое обслуживание и профилактические ремонты, а также изменения значений
величин других элементов, составляющих себестоимость единицы наработки машины.
Экономическими последствиями ненадежности машин являются убытки, которые
возникают в результате простоев машин, рост капитальных вложений в силу
необходимости иметь большее число машин данного назначения и производства
большого количества запасных частей. В работе Р.Н.
Колегаева предлагается единый обобщенный показатель надежности, который позволяет
для различных моделей машин данного функционального назначения дать единую
экономическую оценку надежности. Для этого сравнивается приращение текущих
затрат и капитальных вложений данной машины по отношению к абсолютно надежной
машине этого же вида. При этом абсолютно надежной считается машина, которая
постоянно находится в технически полностью исправном состоянии и обеспечивает
максимально возможную для данной модели производительность, не требуя
проведения ремонтов и технического обслуживания. Значения
экономического показателя надежности определяются по формуле Dснзп
= спзр - спза = (сср - сса) + Ен(сфр
- сфа) = Dсс +
ЕнDсф, (27) где спзр, спза
-
приведенные затраты, приходящиеся на единицу выработки соответственно реальной и
абсолютно надежной машин за оптимальный срок службы, установленный для реальной
машины; сср,
сса - себестоимость единицы наработки соответственно реальной и
абсолютно надежной машин; сфр,
сфа - удельная величина производственных фондов, необходимых для обеспечения
использования реальной и абсолютно надежной машин; Dсс, Dсф - приращение
себестоимости единицы наработки и удельных производственных фондов из-за
ненадежности машин. Производить
окончательную оценку надежности машин необходимо на стадиях их проектирования,
производства и эксплуатации. В зависимости от стадии изменяются содержание и
объем информации, используемой для расчетов Dснзп, однако методика расчета не меняется. 5.2. Для
повышения надежности технологических схем сооружения транспортных тоннелей в
разд. 4 предложено резервирование
механизмов. Однако при этом возрастает стоимость оборудования и требуется
провести экономический анализ с целью оценки эффективности предлагаемой системы
организации работ. Пусть исходная система (без резервирования) имеет стоимость c0 и надежность R0, содержит n подсистем, стоимость каждой машины в которых ci, надежность ri. Тогда
Предположим, что Q0 = 1 - R0 << 1. (30) Допустим, что
каждая машина i-й подсистемы резервируется хi идентичными машинами. Тогда надежность i-й подсистемы
надежность всей
системы
а стоимость всей
системы
Для того чтобы
найти xi при условии, что cp(X) = min и Rp > R, требуется решить вариационную задачу. Для этого нужно ввести
новую переменную ai.
Тогда Надежность
системы
Находится mincp. Можно показать, что
Следовательно,
минимальная стоимость резервирования системы для достижения заданной надежности
R определяется по формуле (36) при числе резервных элементов для
каждой подсистемы, вычисляемых по формуле (35). 5.3. Для
экономической оценки технологической надежности рекомендуется использовать
следующий критерий: W = gDt - f(TтDKп), (39) где g - экономический эффект от работы готового объекта за единицу
времени; f(Dt) - функция, дающая зависимость стоимости строительства от
сокращения времени цикла на Dt (находится эмпирически); Тт - теоретическая
длительность цикла без учета простоев; DKп - уменьшение коэффициента простоя за счет повышения
надежности технологической схемы. Следовательно,
для заданной технологической схемы можно поставить задачу нахождения такого Dt (сокращение времени цикла), при котором W = max. Для различных
технологических схем вместо DKп можно использовать приращение производительности DП. Пусть V - данный объем работ, а П0 - проектная
производительность работ. Тогда Т0 = V/П0 - проектное время работ, а
и, следовательно,
где j(DП) - зависимость
дополнительных затрат от увеличения производительности. Таким образом,
можно искать максимальное значение W в зависимости
от DП. Если П и DП выразить через
другие параметры, то указанный максимум можно искать через эти параметры. Пример расчета
экономической эффективности использования дополнительного парка машин дан в
приложении 5. Приложение 1
ЖУРНАЛ ХРОНОМЕТРАЖНЫХ НАБЛЮДЕНИЙ ЗА РАБОТОЙ
ГОРНО-ПРОХОДЧЕСКОГО ОБОРУДОВАНИЯ
Журнал ведется
отдельно на каждую машину, работающую в забое. На обложке журнала
указываются выходные данные машины и место ее работы. 1. В гр. 2
указываются конкретные часы и минуты работы, например: 10.03.83 с 7-00 до
12-15. 2. В гр. 3
приводится конкретное время простоя механизма, обусловленного технологией работ
(в соответствии с циклограммой, т.е. запланированное), например: 10.03.83 с
12-15 до 13-05. 3. В гр. 4
указывается конкретное время простоя механизма из-за поломки
(незапланированное), например: 10.03.83 с 15-00 до 17-00. В гр. 5 дается
установленная причина поломки, например: «Сломалась левая лапа погрузочной
машины». 4. В гр. 6
указывается время, когда приступили к ликвидации поломки и когда этот ремонт
закончили; например: 10.03.83 сломанную лапу начали ремонтировать путем
приваривания в 15-32 и закончили в 17-13. 5. В гр. 7
заносится конкретное время профилактического ремонта, а также его содержание
(гр. 8); например: 12.03.83 с 20-05 до 21-12 провели техосмотр и смазку
подшипников ведущего вала. 6. В гр. 8
указывается время начала и конца замены отказавшей машины на резервную, если
такая имеется; например: 15.03.83 в 10-45 начали замену машины, за которой
ведутся наблюдения (№ 00035 условно), резервной (№ 00138 условно) и закончили в
11-10. 7. В гр. 9 и 10
приводится время начала и конца простоя машины по организационным причинам и
указывается эта причина; например: 17.03.83 из-за отсутствия автобуса для
доставки рабочих утренней смены машина простаивала с 8-00 до 9-15. 8. В гр. 11
дается время начала и конца каждой технологической операции, выполненной в
данной смене; например: бурение с 8-00
до 12-00, взрывание с 12-15 до 12-35, уборка породы с 12-35 до 14-00. 9. В гр. 12
указывается, кто вел хронометражные наблюдения, а также приводятся другие
сведения, которые наблюдающий сочтет необходимыми. Приложение 2
ПРИМЕР РАСЧЕТА КОМПЛЕКСНОГО ПОКАЗАТЕЛЯ ДЛЯ ОЦЕНКИ УРОВНЯ
ТЕХНОЛОГИЧЕСКОЙ СХЕМЫ
В данном примере
рассматриваются четыре технологические схемы для проходки однопутного
железнодорожного тоннеля в устойчивых грунтах средней крепости: схема 1 -
буровзрывным методом на полный профиль (lзах = 3 м, S = 50 м2)
с применением бурового агрегата для комплексного машинного обуривания забоя и
механизацией операций заряжания шпуров и возведения анкерной крепи, причем
крепление совмещается с обуриванием забоя; уборка грунта производится машиной
ПНБ-3Д в вагоны ВПК-10; схема 2 -
буровзрывным методом способом опертого свода с применением самоходных кареток
для бурения шпуров в забое калотты и скважин на уступе (каждая
производительностью по Птм = 7 м/ч); крепление выработки осуществляется арками с затяжкой стен
и последующим бетонированием, уборка грунта - с помощью машины ПНБ-3Д и вагонов
ВПК-10 на нижнем горизонте и машины ПНБ-3Д и самоходного вагона на верхнем
горизонте; схема 3 -
механизированным щитом диаметром 8,5 м с железобетонной сборной обделкой
толщиной 30 см; схема 4
(эталонная) - тоннелепроходческой машиной диаметром 8,2 м с креплением
выработки набрызг-бетоном толщиной 15 см робот-методом одновременно с
разработкой грунта. Требуется
определить основные параметры технологических схем и оценить их уровень относительно
эталонной технологии. Опуская промежуточные вычисления, представим результаты
расчета в табличной форме.
Уменьшая простои
комплексов от приведенных в примере значений до нуля, можно существенно повысить
производительность технологической схемы, а значит, и ее уровень. При этом
возможна ситуация, когда буровзрывной способ способен конкурировать по
эффективности с механизированным, даже при меньших скоростях проходки. Использование
комплексного показателя не только позволяет обоснованно выбирать или
проектировать лучшую из возможных технологическую схему и поддерживать на
высоком уровне показатели, но также анализировать и оценивать эффективность
расчетных и фактических значений производительности Приложение 3
ПРИМЕРЫ РАСЧЕТА ОПТИМАЛЬНОГО ПЕРИОДА ПРОФИЛАКТИЧЕСКИХ
РЕМОНТОВ
Пример
1 (к п.3.2). Хронометражные наблюдения за работой комплекса для
возведения набрызг-бетонной крепи дали следующие результаты: среднее время
безотказной работы узла для приготовления сухой смеси Тср = 50 ч; время
технологического перерыва р = 6 ч; время работы узла
между технологическими перерывами r = 10 ч; средняя
длительность аварийного ремонта а = 10 ч; средняя
длительность полного профилактического ремонта S = 8 ч. Так как плотность
потока отказов растет с течением времени, то в качестве закона распределения времени
безотказной работы можно принять закон Вейбулла, для которого Найдем l0 для закона
Вейбулла из условия
Интеграл
вычисляем по формуле
где Для расчета
оптимального числа полных рабочих периодов между профилактиками m* и минимума коэффициентов простоя K(t) применяем
программу T1SPR1. Исходные данные: А = 10,0; Т = 50,0; R = 10,0; d = 2,0. Результаты: Количество итераций J = 3. Начальное
значение для поиска «М» М1 = 1. Число полных
рабочих периодов М = 3. Коэффициент
простоя SK1 = 0,1452. Следует
отметить, что без профилактики K(t) = 0,2. Пример
2 (к п. 3.3). Рассмотрим работу горнопроходческого комплекса,
состоящего из бурового агрегата А и погрузочной машины Б. Работа этих
механизмов осуществляется последовательно, и любая неисправность агрегата при
нахождении его в забое должна быть устранена немедленно, прежде чем будет
произведен взрыв и в забой будет введена погрузочная машина. Возьмем
следующие данные: среднее время
безотказной работы бурового агрегата Тср = 35 ч; средняя
длительность плановой профилактики время
технологического перерыва p = 6 ч; средняя
длительность аварийного ремонта a = 9 ч; время работы
между технологическими перерывами r = 5 ч; время работы до
первого аварийного ремонта r¢ = 3 ч. Выбрав закон
Вейбулла
Примем программу
T1SPR1. Исходные данные: А = 9,0; Т = 35,0; R = 5,0; S = 2,0. Результаты: Количество итераций J = 4. Начальное
значение для поиска «М» М1 = 1. Число полных
рабочих периодов М = 4. Коэффициент
простоя SK1 = 0,1960. Для определения
оптимального числа m* полных периодов между аварийным
и профилактическим ремонтами вычисляем для ряда значений Принимая Следует отметить,
что без профилактических ремонтов
Пример
3 (к п. 3.4). Погрузочно-транспортный комплекс состоит из погрузочной
машины А и транспортера с бункером-накопителем Б, откуда грунт поступает в
транспортные средства. В этом случае при отказе погрузочной машины уборка
грунта часть времени (или все время), необходимого для аварийного ремонта, не
прекращается, так как находящийся на транспортере и в бункере грунт продолжает
поступать в транспортные сосуды. Пусть для
погрузочной машины Тср = 40 ч; Тогда l0 = 0,0005; q = р/r = 2; S = 0,5 ч; a > qr. Для расчета
оптимального периода m* применяем
программу T1SPR2. Исходные данные: А = 7,5; Т = 40,0; R = 3,0; S = 0,5; p = 6,0. Результаты: Количество итераций J = 6. Начальное
значение для поиска «М» М1 = 1. Число полных
рабочих периодов М = 6. Коэффициент
простоя SK1 = 0,0756. Пример 4 (к п. 3.5). Рассмотрим
работу бетоно-смесительного узла, состоящего из устройств для подачи материалов
(заполнителей, цемента и воды) А1 через расходные бункеры в
бетоносмеситель А2, из которого готовая бетонная смесь через
расходные бункеры А3 перегружается в транспортные сосуды для
доставки к месту бетонирования. При неисправности любого из устройств Ai весь узел останавливается и возобновляет работу после
ремонта отказавшего устройства. При этом устройства комплекса, следующие по
технологическому процессу после ремонтируемого, сначала принимают дозу
материалов или бетонной смеси, находившихся в ремонтируемом устройстве до его
аварийной остановки, перерабатывают ее, а затем продолжают рабочий цикл. На
основе хронометражных наблюдений нами получены следующие данные, в часах,
(таблица).
Применим
программу T1SPR1. Исходные данные: А = 2,0; Т = 70,0; R = 16,0; S = 0,5. Результаты: Количество итераций J = 3. Начальное значение
для поиска «М» М1 = 1. Число полных
рабочих периодов М = 3. Коэффициент
простоя SK1 = 0,0228. Исходные данные: А = 4,0; Т = 100,0; R = 24,0; S = 0,5. Результаты: Количество итераций J = 2. Начальное
значение для поиска «М» М1 = 1. Число полных рабочих
периодов М = 2. Коэффициент
простоя SK1 = 0,0239. Исходные данные: А = 5,0; Т = 50,0; R = 24,0; S = 1,0. Результаты: Количество итераций J = 1. Начальное
значение для поиска «М» М1 = 1. Число полных
рабочих периодов М = 1. Коэффициент
простоя SK1 = 0,0736. Отсюда по формуле
(11) Кпкомп =
0,1550. Приложение 4
ПРИМЕР РАСЧЕТА ОПТИМАЛЬНОГО КОЛИЧЕСТВА РЕЗЕРВНЫХ МАШИН
В
технологическом процессе по строительству тоннеля буровзрывным способом
участвуют четыре типа машин: экскаватор фирмы «Като», самосвальный автопоезд
МоА3-64011-9585, зарядодоставочная машина типа «Ульба», бульдозер Т-130.
Стоимость каждого вида машин соответственно 150 тыс. руб., 35 тыс. руб., 8 тыс.
руб. и 19 тыс. руб., а надежность - 0,85; 0,92; 0,72; 0,89. На строительстве
данного забоя ограничение на стоимость проектируемой техники составило 500 тыс.
рублей. Необходимо распределить количество резервных машин каждого типа так, чтобы
надежность технологической схемы была максимальной (или коэффициент потерь
минимальным) при данных ограничениях на затраты. Применим
программу Т1MRV1. Исходные данные: количество подсистем 4; количество ограничений 1; допустимая
погрешность на надежность 0,01; значения ограничений на затраты 500000; матрица
значений затрат 150000; 35000; 8000; 19000; надежность элементов по подсистемам
0,85; 0,92; 0,72; 0,89; допустимая погрешность на затраты 3000. Результаты
расчета по критерию надежности технологической схемы приведены в табл. 1. Таблица 1
Общая надежность
системы Р = 0,964. Общая стоимость оборудования С1 = 459 тыс. руб. Результаты
расчета по критерию коэффициента простоя приведены в табл. 2. Таблица 2
Общий
коэффициент простоя К = 0,03; общая стоимость оборудования С1 = 478
тыс. руб. Приложение 5
ПРИМЕР РАСЧЕТА ЭКОНОМИЧЕСКОЙ ЭФФЕКТИВНОСТИ ПОВЫШЕНИЯ
ТЕХНОЛОГИЧЕСКОЙ НАДЕЖНОСТИ
Найти количество
дополнительных машин, которое нужно ввести в строительство, чтобы прибыль была
максимальной, если каждая дополнительная машина имеет производительность П1,
а стоимость ее аренды и эксплуатации за все время работы составит r рублей. Количество
дополнительных машин
Тогда
где Отсюда из
условия W¢ = 0 найдем
оптимальное значение DП*
Так, если Т0
= 50 дней, П0 = 60 м/день, g = 1000 руб./день, r = 500 руб., DП1 =
5 м/день, то DП* = 35 м и,
следовательно, n* = 35:5 = 7 (машин). СПИСОК ЛИТЕРАТУРЫ
1. Гнеденко
Б.В., Беляев Ю.К., Соловьев А.Д. Математические методы и теории надежности. М.,
Наука, 1965. 2. Козлов Б.А.,
Ушаков И.А. Справочник по расчету надежности. М., Советское радио, 1975. 3. Барлоу Р.,
Прошан Ф. Математическая теория надежности. М., Советское радио, 1969. 4. О надежности
сложных технических систем. М., Советское радио, 1966. 5. Федоров Д.
И., Бондарович Б.А. Надежность рабочего оборудования землеройных машин. М.,
Машиностроение, 1981. 6. Котляревский
Г.П. Основы повышения надежности и долговечности горно-шахтного оборудования.
М., Недра, 1971. 7. Воробьев Б.М.
и др. Надежность технологических схем и процессов угольных шахт. М., Недра, 1975. 8.
Алгоритмические методы в теории надежности, Киев, изд. ИК АН УССР, 1974. 9. Королюк В.С.,
Турбин А.Ф. Полумарковские процессы и их приложения. Киев, Наукова думка, 1976. 10. Сандлер Дж.
Техника надежности систем. М., Наука, 1966. 11. Войнов К.Н.
Прогнозирование надежности механических систем. Л., Машиностроение, 1978. 12. Рахутин Г.С.
Вероятностные методы расчета надежности, профилактики и резерва горных машин.
М., Наука, 1969. 13. Бескровный
Н.Т. Экономика и оптимизация оборудования. М., Недра, 1974. 14. Шендеров
А.И., Емельянов О.А., Один И.М. Надежность и производительность комплекса
горно-транспортного оборудования. М., Недра, 1976. 15. Колегаев
Р.Н. Экономическая оценка качества и оптимизация системы ремонта машин. М.,
Машиностроение, 1980. 16. Кулаков
Н.Н., Загоруйко А.О. Методы оценки повышения надежности технических изделий по
технико-экономическим показателям. Новосибирск, Наука, 1969. 17. Основные
вопросы теории и практики надежности. М., Советское радио, 1980. 18. Гаркави
А.Л., Афендиков Л.С., Маневич И.З., Меркин В.Е. Оптимизация периода
профилактики и ее влияние на производительность и надежность
горно-проходческого оборудования. - Транспортное строительство, 1983, № 1. 19. Гаркави
А.Л., Афендиков Л.С., Маневич И.З., Меркин В.Е. Об оптимальном режиме,
профилактике горно-проходческого оборудования. - Транспортное строительство,
1983, № 4. 20. Гаркави
А.Л., Афендиков Л.С., Маневич И.З., Меркин В.Е. Об эффективности резервирования
механизмов горно-проходческих комплексов. - Транспортное строительство, 1983, №
6. 21. Гаркави
А.Л., Афендиков Л.С., Маневич И.З., Меркин В.Е. Оптимальное резервирование
механизмов горно-проходческих комплексов. - Транспортное строительство, 1984, №
5. 22. Меркин В.Е. Комплексный
критерий оценки уровня технологических схем. - Транспортное строительство,
1984, № 2. 23. Гарбер В.А.,
Евдокимова М.Б., Маневич И.З., Шостаковская О.Г. Вычисление оптимального
периода профилактики машин и механизмов (Т1SPR1). Программа № ПОО7586, сданная в ГосФАП. 24. Маневич
И.З., Меркин В.Е., Проскурия Л.Л. Оптимальное резервирование машин и механизмов
при наличии линейных ограничений (Т1SPR2). Программа №
ПОО7318, сданная в ГосФАП. СОДЕРЖАНИЕ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|