Р 50.2.038-2004
РЕКОМЕНДАЦИИ ПО МЕТРОЛОГИИ
Государственная
система обеспечения
единства измерений
ИЗМЕРЕНИЯ ПРЯМЫЕ
ОДНОКРАТНЫЕ
Оценивание погрешностей и
неопределенности
результата измерений
ГОССТАНДАРТ РОССИИ
Москва
Предисловие
1 РАЗРАБОТАНЫ Федеральным государственным унитарным предприятием
Всероссийский научно-исследовательский институт метрологии им. Д.И. Менделеева
Госстандарта России (ФГУП ВНИИМ им. Д.И. Менделеева)
ВНЕСЕНЫ Управлением метрологии Госстандарта России
2 УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Приказом Федерального агентства по
техническому регулированию и метрологии от 27 октября 2004 г. № 43-ст
3 ВЗАМЕН МИ 1552-86
СОДЕРЖАНИЕ
РЕКОМЕНДАЦИИ ПО МЕТРОЛОГИИ
Государственная система
обеспечения единства измерений
ИЗМЕРЕНИЯ ПРЯМЫЕ ОДНОКРАТНЫЕ
Оценивание погрешностей и неопределенности
результата измерений
State system for ensuring the uniformity of
measurements.
Direct single measurements. Estimation of errors and uncertainty of
measurements result
Дата введения 2005-01-01
1 Область применения
Настоящие рекомендации распространяются
на нормативные, конструкторские, технические и другие документы,
устанавливающие методики выполнения измерений (МВИ), и содержат методы
оценивания характеристик погрешности и неопределенности результатов прямых
однократных измерений. Разрабатываемые МВИ должны соответствовать требованиям ГОСТ Р 8.563.
Пример оценивания
погрешности однократного измерения приведен в приложении А.
2 Нормативные ссылки
В настоящих рекомендациях
использованы ссылки на следующие нормативные документы:
ГОСТ
8.207-76 Государственная система обеспечения единства измерений. Прямые
измерения с многократными наблюдениями. Методы обработки результатов
наблюдений. Основные положения
ГОСТ
8711-93 (МЭК
51-2-84) Приборы аналоговые показывающие электроизмерительные прямого
действия и вспомогательные части к ним. Часть 2. Особые требования к
амперметрам и вольтметрам
ГОСТ Р 8.563-96 Государственная
система обеспечения единства измерений. Методики выполнения измерений
РМГ
43-2001 Государственная система обеспечения единства измерений. Применение
«Руководства по выражению неопределенности измерений»
РД
50-453-84 Характеристики погрешности средств измерений в реальных условиях
эксплуатации. Методы расчета
МИ
1317-86 Государственная система обеспечения единства измерений. Результаты
и характеристики погрешности измерений. Формы представления. Способы
использования при испытаниях образцов продукции и контроле их параметров
3 Термины, определения, обозначения и сокращения
3.1 В настоящих рекомендациях применяют следующие термины с
соответствующими определениями:
границы неисключенной
систематической погрешности измерений: Границы интервала, внутри которого находится
неисключенная систематическая погрешность измерений.
однократное измерение: Измерение, выполненное один
раз.
неопределенность
(измерений): Параметр,
связанный с результатом измерений и характеризующий рассеяние значений, которые
могли бы быть обоснованно приписаны измеряемой величине (по РМГ 43).
стандартная неопределенность
и (измерений): Неопределенность результата измерений, выраженная в виде среднего квадратического
отклонения (по РМГ
43).
Примечания
1 Стандартную неопределенность, оцениваемую по типу А, uA вычисляют по формуле
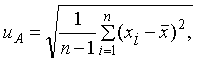 (1)
(1)
где ![]() - среднее
арифметическое экспериментальных данных, полученных при измерении (по РМГ
43).
- среднее
арифметическое экспериментальных данных, полученных при измерении (по РМГ
43).
2 Стандартную неопределенность, оцениваемую по типу В, uB вычисляют по формуле
где Θ - неисключенная систематическая погрешность, заданная границами ±Θ (по РМГ 43).
суммарная стандартная
неопределенность uc (измерений): Стандартная неопределенность результата измерений, равная положительному
квадратному корню суммы дисперсий (по РМГ
43).
расширенная неопределенность
U (измерений): Границы интервала, в
пределах которого находится большая часть распределения значений, которые могли бы быть
приписаны измеряемой величине.
3.2 В настоящих
рекомендациях использованы следующие сокращения:
- СИ - средство измерений;
- НСП - неисключенная систематическая погрешность;
- СКО - среднее
квадратическое отклонение.
3.3 В настоящих
рекомендациях использованы следующие обозначения:
à - результат однократного
измерения;
xi - i-е
экспериментальное данное, полученное при измерении;
![]() - среднее арифметическое
значение экспериментальных данных;
- среднее арифметическое
значение экспериментальных данных;
и - стандартная неопределенность
измерений;
uA - стандартная
неопределенность, оцениваемая по типу А;
uB - стандартная неопределенность,
оцениваемая по типу В;
uc - суммарная стандартная
неопределенность;
U
- расширенная
неопределенность;
U(Р)
- расширенная неопределенность для уровня доверия Р;
k -
поправочный коэффициент при суммировании НСП, определяемый принятой доверительной
вероятностью Р и числом т составляющих
Θj;
kо -
коэффициент охвата;
К - коэффициент, используемый
при суммировании систематической и случайной составляющих погрешности;
S(Ã)
- СКО случайной погрешности результата измерений;
S -
СКО единичного измерения при многократных измерениях;
D(Р) - доверительные границы суммарной погрешности результата измерений для
доверительной вероятности Р;
zP/2 - квантиль нормального распределения для доверительной
вероятности Р;
Θ - границы неисключенной
систематической погрешности;
Θ(Р) - доверительные
границы систематической погрешности измерения для доверительной вероятности Р;
п - число экспериментальных
данных;
т - число суммируемых НСП;
e(Р) -
доверительные границы случайных погрешностей.
4 Общие положения
4.1 За результат
однократного измерения Ã принимают значение величины, полученное
при измерении.
4.2 На этапе перехода от
погрешности к неопределенности целесообразно указывать характеристики и погрешности,
и неопределенности результата измерения.
Составляющие погрешности
результата измерения должны быть известны до проведения измерения.
Предполагают, что известные систематические погрешности исключены (внесены
поправки на все известные источники неопределенности, имеющие систематический
характер).
4.3 Полагают, что
распределение случайных погрешностей не противоречит нормальному распределению,
а неисключенные систематические погрешности, представленные заданными границами
±Θ, распределены равномерно.
Неопределенность результата
измерений понимают как неполное знание значения измеряемой величины, и для
количественного выражения этой неполноты вводят распределение вероятностей
возможных значений измеряемой величины - параметр, который количественно характеризует
точность результата измерений. Полагают, что распределение вероятностей
возможных значений измеряемой величины не противоречит нормальному
распределению.
В целях количественного
выражения неопределенности результата измерения, представленной в виде границ
отклонения значения величины от ее оценки [- Θ; + Θ] (неполное знание
о значении величины), полагают, что распределение возможных значений измеряемой
величины в указанных границах не противоречит равномерному распределению.
4.4 Выполнение однократных
измерений обосновывают следующими факторами:
- производственной
необходимостью (разрушение образца, невозможность повторения измерения,
экономическая целесообразность и т.д.);
- возможностью пренебрежения
случайными погрешностями;
- случайные погрешности
существенны, но доверительная граница погрешности результата измерения не
превышает допускаемой погрешности измерений;
- стандартная
неопределенность, оцениваемая по типу А, существенна, но расширенная неопределенность
не превышает заданного предела.
Примечания
1 Случайные погрешности считают пренебрежимо малыми по сравнению с неисключенными систематическими, если
Θ/S(Ã) > 8, (3)
где Θ - граница НСП результата измерения;
S(Ã) - СКО случайных погрешностей результата измерения.
2 Неопределенность, оцениваемую по типу А, считают пренебрежимо малой по сравнению с неопределенностью, оцениваемой по типу В, если выполняется условие
 (4)
(4)
где uA и uB - стандартные неопределенности, оцениваемые по типам А и В соответственно.
4.5 При определении доверительных границ погрешности или расширенной
неопределенности для уровня доверия Р результата измерения принимают
вероятность, равную 0,95.
В особых случаях, например
при измерениях, которые нельзя повторить, допускается указывать доверительные
границы или расширенную неопределенность для уровня доверия Р и более
высоких вероятностей.
4.6 При вычислениях следует
пользоваться правилами округления в соответствии с МИ
1317. Доверительные границы погрешности (характеристики погрешности) и
расширенная неопределенность (расширенная неопределенность для уровня доверия Р)
результата измерения должны быть представлены не более чем двумя значащими
цифрами.
5 Составляющие погрешности и неопределенности результата
измерения
5.1 Составляющими
погрешности результата однократного измерения являются погрешности СИ, метода,
оператора, а также погрешности, обусловленные изменением условий измерения.
5.2 Погрешность результата
однократного измерения чаще всего представлена НСП и случайными погрешностями.
Неопределенность результата
однократного измерения может быть представлена стандартными неопределенностями,
оцениваемыми по типам А и В.
5.3 Характеристикой НСП
могут быть:
- границы ±Θ;
- доверительные границы ±Θ(Р).
5.4 Характеристикой
случайных погрешностей могут быть:
- СКО S;
-
доверительные
границы ±e(Р).
5.5 Погрешность СИ
определяют на основании их метрологических характеристик, которые должны быть
указаны в нормативных и технических документах, и в соответствии с РД
50-453.
5.6 Погрешности метода и
оператора должны быть определены при разработке и аттестации конкретной МВИ.
6
Оценивание неисключенной систематической погрешности и стандартной
неопределенности, оцениваемой по типу В, результата измерения
6.1 НСП результата измерения
выражают границами этой погрешности, если среди составляющих погрешности
результата измерения в наличии одна НСП.
При указанном выше условии
стандартную неопределенность uB, обусловленную неисключенной систематической погрешностью, заданной
своими границами ±Θ, оценивают по формуле (2).
6.2 Доверительные границы НСП
результата измерения вычисляют следующим образом.
6.2.1
При наличии нескольких НСП, заданных своими границами ±Θj, доверительную границу НСП
результата измерения Θ(Р) (без учета знака) вычисляют по
формуле
где k - поправочный коэффициент,
определяемый принятой доверительной вероятностью и числом т составляющих
Θj.
При доверительной
вероятности Р = 0,95 поправочный коэффициент k принимают равным 1,1.
При доверительной
вероятности Р = 0,99 поправочный коэффициент k принимают равным 1,45, если
число суммируемых составляющих т > 4. Если же число составляющих
равно четырем (т = 4), то поправочный коэффициент k
≈ 1,4;
при т = 3 k ≈ 1,3; при т = 2 k
≈
1,2. Более точное значение k для доверительной
вероятности Р = 0,99 при числе составляющих т £ 4 в зависимости от
соотношения составляющих l
определяют по графику [k = f(m,
l)] в соответствии с требованиями ГОСТ
8.207.
Примечание - Погрешность, возникающая при использовании
формулы (5)
для суммирования НСП и при нахождении поправочного коэффициента k для доверительной вероятности Р = 0,99
по графику [k = f(m,
l)], не
превышает 5 %.
При условии, указанном в 6.2.1,
суммарную стандартную неопределенность, оцениваемую по типу В, ис,
B вычисляют по формуле
 (6)
(6)
6.2.2 При наличии нескольких
НСП, заданных доверительными границами Θj(Рi), рассчитанными по
формуле (5),
доверительную границу НСП результата однократного измерения вычисляют по
формуле
 (7)
(7)
При условии, указанном выше,
суммарную стандартную неопределенность, оцениваемую по типу В, вычисляют по
формуле
 (8)
(8)
где Θj(Pi) - доверительная
граница j-й НСП, соответствующая
доверительной вероятности Рi;
k и ki - коэффициенты, соответствующие доверительным
вероятностям Р и Рi.
Значения коэффициентов k и ki определяют в соответствии с требованиями 6.2.1.
7
Оценивание случайной погрешности и стандартной неопределенности, оцениваемой по
типу А, результата измерения
7.1 Доверительные границы
случайной погрешности и стандартную неопределенность, оцениваемую по типу А,
результата измерения вычисляют следующим образом.
7.1.1
Если случайные погрешности представлены несколькими СКО Si, то СКО результата
однократного измерения S(Ã) вычисляют по формуле
 (9)
(9)
Учитывая условия 7.1.1,
стандартную неопределенность, оцениваемую по типу А, результата однократного
измерения иA вычисляют по формуле

![]() (10)
(10)
где т - число составляющих случайных
погрешностей;
ui,A = Si.
Доверительную границу
случайной погрешности результата измерения e(Р) вычисляют
по формуле
e(P) = ZP/2S(Ã), (11)
где ZP/2 - Р/2 точка
нормированной функции Лапласа, отвечающая вероятности Р. При
доверительной вероятности Р = 0,95Z0,95/2 принимают равным 2, при Р
= 0,99Z0,99/2 = 2,6.
7.1.2 Если случайные
погрешности представлены доверительными границами ei(Р), соответствующими одной и той же вероятности, доверительную границу
случайной погрешности результата однократного измерения вычисляют по формуле
 (12)
(12)
7.1.3 Если случайные
погрешности представлены доверительными границами, соответствующими разным
вероятностям, сначала определяют СКО результата измерения по формуле
 (13)
(13)
а затем вычисляют доверительные границы случайной
погрешности результата измерения по формуле (11).
8
Оценивание погрешности и расширенной неопределенности результата измерения
8.1 Если погрешности метода
и оператора пренебрежимо малы по сравнению с погрешностью используемых СИ (не
превышают 15 % погрешности СИ),
то за погрешность результата измерения принимают погрешность используемых СИ.
8.2 Если ![]() , то НСП или стандартной неопределенностью, оцениваемой по
типу В, пренебрегают и принимают в качестве погрешности или неопределенности
результата измерения доверительные границы случайных погрешностей или
расширенную неопределенность для уровня доверия Р, вычисляемую по
формуле U(P) = kоиА.
, то НСП или стандартной неопределенностью, оцениваемой по
типу В, пренебрегают и принимают в качестве погрешности или неопределенности
результата измерения доверительные границы случайных погрешностей или
расширенную неопределенность для уровня доверия Р, вычисляемую по
формуле U(P) = kоиА.
Если ![]() , то случайными погрешностями или стандартной
неопределенностью, оцениваемой по типу А, пренебрегают и принимают в качестве
погрешности или неопределенности результата измерения границы НСП или
расширенную неопределенность для уровня доверия Р, вычисляемую по
формуле U(P) = kоиB.
, то случайными погрешностями или стандартной
неопределенностью, оцениваемой по типу А, пренебрегают и принимают в качестве
погрешности или неопределенности результата измерения границы НСП или
расширенную неопределенность для уровня доверия Р, вычисляемую по
формуле U(P) = kоиB.
8.3 Если ![]() , то доверительную границу погрешности результата измерений D(Р) вычисляют по формуле
, то доверительную границу погрешности результата измерений D(Р) вычисляют по формуле
D(P) = K[Θ(P) + e(P)], (14)
где К - коэффициент, значение которого для
доверительной вероятности 0,95 равно 0,76; для доверительной вероятности 0,99
значение коэффициента K
равно 0,83.
Расширенную неопределенность
для уровня доверия Р вычисляют по формуле
![]() (15)
(15)
где ko - коэффициент охвата
(коэффициент, используемый как множитель суммарной неопределенности для
получения расширенной неопределенности). Значение коэффициента охвата для
доверительной вероятности Р = 0,95 считают равным 2, для доверительной
вероятности Р = 0,99 - равным 3.
9 Форма представления
результата измерения
9.1 Форма представления
результатов однократных измерений должна соответствовать МИ
1317.
9.2 При симметричной
доверительной погрешности результат однократного измерения представляют в форме
Ã; ±D(Р); Р или Ã;
±D(Р), или Ã;U(Р).
Значение результата
измерения должно оканчиваться цифрами того же разряда, что и значение
погрешности или расширенной неопределенности для уровня доверия.
ПРИЛОЖЕНИЕ А
(справочное)
Расчет погрешности измерения
напряжения показывающим прибором
Однократное измерение
напряжения на участке электрической цепи сопротивлением R =
4 Ом.
А.1 Априорные данные об
исследуемом объекте
Участок электрической цепи
представляет собой соединение нескольких резисторов, имеющих стабильное
сопротивление. Ток в цепи - постоянный. Измерение выполняют в сухом
отапливаемом помещении температурой до 30 °С при магнитном поле до 400
А/м. Предполагаемое падение напряжения на участке цепи, не превышающее 1,5 В,
постоянно.
Для измерения выбирают
вольтметр класса точности 0,5 по ГОСТ
8711 (приведенная погрешность 0,5 %) с верхним пределом диапазона измерений
Uпp = 1,5 В. Вольтметр имеет
магнитный экран. Некоторый запас по точности средства измерений необходим из-за
возможного наличия дополнительных погрешностей, погрешности метода и т.д.
Инструментальная
составляющая погрешности определяется основной и дополнительной погрешностями.
Основная погрешность прибора
указана в приведенной форме. Следовательно,
предел допускаемой основной погрешности вольтметра
![]()
Дополнительная погрешность
из-за влияния магнитного поля не превышает 1,5 % нормирующего значения прибора
и равна ±0,0225 В (0,015 · 1,5). Дополнительная температурная погрешность,
обусловленная отклонением температуры от нормальной (20 °С) на 10 °С, не
превышает 60 % предела
допускаемой основной погрешности, эта дополнительная погрешность равна ±0,0045
В (0,0075 · 0,6).
А.2
Оценивание погрешности результата измерения
Погрешность метода
определяется соотношением между сопротивлением участка цепи R и
сопротивлением вольтметра RV. Сопротивление вольтметра
известно: RV = 1000 Ом. При подсоединении
вольтметра к цепи исходное напряжение Ux изменяется на
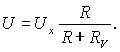
Отсюда методическая
погрешность DM
в абсолютной форме

Методическая погрешность
δм в относительной форме
![]()
Оцененная методическая
погрешность является систематической составляющей погрешности измерений и
должна быть внесена в результат измерения в виде поправки ![]() В. Тогда результат
измерения Ã с учетом поправки на
систематическую погрешность
В. Тогда результат
измерения Ã с учетом поправки на
систематическую погрешность
à = 0,90 + 0,004 = 0,904 В.
Находят границы погрешности
результата измерения.
Поскольку основная
погрешность применяемого средства измерений и его дополнительные погрешности
заданы границами, следует рассматривать эти погрешности как неисключенные систематические.
Воспользовавшись формулой (5), находят доверительную границу неисключенной
систематической погрешности результата измерения при доверительной вероятности Р
= 0,95:
![]()
Результат измерения в
соответствии с разделом 9 следует представить в форме
à = 0,904 В; D(Р) = ±0,027 В; Р = 0,95
или (0,904 ± 0,027) В; Р = 0,95.
Ключевые слова: результат измерения,
однократные измерения, среднее квадратическое отклонение, стандартная
неопределенность, оцениваемая по типу А и по типу В, доверительная погрешность,
расширенная неопределенность, коэффициент охвата, неисключенная систематическая
погрешность
