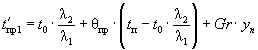Министерство строительства предприятий тяжелой
индустрии СССР

Проектный и научно-исследовательский институт
«КРАСНОЯРСКИЙ ПРОМСТРОЙНИИПРОЕКТ»

ПРАКТИЧЕСКОЕ РУКОВОДСТВО
ПО ПРОИЗВОДСТВУ ТЕПЛОВЫХ РАСЧЕТОВ ОСНОВАНИЙ
В РАЙОНАХ С ВЕЧНОМЕРЗЛЫМИ ГРУНТАМИ

Красноярск

1976

В Руководстве освещаются практические методы определения температурных полей оснований, а также обуславливающих их составляющих внешнего теплообмена и теплофизических характеристик. Знание этих величин необходимо для проектирования фундаментов в соответствии с главой СНиП II-Б.6-66 «Основания и фундаменты зданий и сооружений на вечномерзлых грунтах».

Руководство предназначается для изыскателей и проектировщиков, связанных с работой в районах с вечномерзлыми грунтами и глубоким сезонным промерзанием.

Руководство написано канд. геогр. наук А.А. Коноваловым. В составлении II раздела принимали участие канд. физ.-мат. наук А.Г. Конюшенко и инж. Л.А. Наумова.

ВВЕДЕНИЕ

Одним из основных этапов проектно-изыскательских работ в районах с вечномерзлыми грунтами или глубоким сезонным промерзанием (южная граница этих районов проходит примерно по изолинии среднегодовой температуры воздуха минус 1 °С) является производство тепловых расчетов, связанных с определением температурных полей грунта или обуславливающих его величин - составляющих внешнего теплообмена и теплофизических характеристик грунта. Методика большей части этих расчетов изложена в соответствующих нормативных документах.

Однако практика и дальнейшее развитие теории ставят перед проектировщиками новые задачи в области тепловых расчетов, прикладное решение которых раньше не являлось первой необходимостью. Например, для расчета несущей способности грунтового основания по существующей главе СНиПа II-Б.6-66 достаточно знать его стационарное (предельное, при стремлении времени к бесконечности) температурное поле. В то же время известно, что предельно-длительные сопротивления мерзлого грунта зависят от температуры, изменяющейся во времени. Но поскольку не было известно, как учитывать при определении сопротивлений изменение температуры во времени, не возникало потребности в расчете нестационарных температурных полей в основаниях зданий и сооружений. В настоящее же время, когда получено [1] уравнение для предельно-длительных сопротивлений, в которое температура входит как функция времени, появилась необходимость в разработке методов расчета нестационарных температурных полей.

Представляется также важным на базе существующих решений создать унифицированную, максимально приспособленную для практического применения методику расчета температурных полей грунта под естественными и искусственными тепловыми источниками (или стоками) наиболее типичных геометрических форм и режимов теплообмена. В настоящем Руководстве предпринята попытка отработки такой методики.

Руководство состоит из 6 разделов с приложениями. В I разделе приводится перечень исходных и искомых величин, их условных обозначений. Для искомых величин указывается номер пункта, в котором излагается способ их определения. Следует отметить, что одни и те же переменные могут быть как исходными, так и искомыми величинами, это зависит от условий конкретной задачи. Поэтому в перечне не проводится грани между исходными и искомыми величинами.

Методика определения стационарных и нестационарных температурных полей грунта (в том числе с учетом фазовых превращений грунтовой влаги, возбуждаемых тепловыми источниками различной конфигурации) освещается во 2 и 3 разделах Руководства.

Необходимость в определении стационарных полей возникает при установлении расчетных (наихудших) условий проектирования фундаментов на мерзлых грунтах, используемых по принципу I (СНиП II-Б.6-66); при вычислении предельной глубины оттаивания; при расчете температур под естественными источниками (водоемами, различными типами местности и т.д.).

Стационарные (предельные) температуры, кроме того, в любом случае, определяется в качестве исходных величин при расчете нестационарных температурных полей.

Нестационарные температурные поля определяются для расчета предельно-длительных сопротивлений мерзлого грунта с учетом меняющейся во времени температуры, определения осадок оттаивающих оснований при расчете фундаментов по принципу II, прогнозирования изменения температурного режима грунтов на осваиваемой территории и т.п.

Инженерные сооружения, водоемы, участки с измененными условиями теплообмена на поверхности и др., в дальнейшем для краткости именуемые тепловыми источниками, обычно имеют правильную (симметричную относительно центральной оси) геометрическую форму. Если исключить некоторые частности, то все разнообразие встречающихся конфигураций таких источников можно разбить на три группы:

а) наземные (поверхностные) источники в форме бесконечной полосы, прямоугольников с различными соотношениями длины и ширины, круга;

б) их заглубленные или приподнятые над общей поверхностью грунта аналоги в форме, соответственно, горизонтального бруса бесконечной длины, три грани которого находятся в грунте, - для заглубленного аналога, или - лежат выше общей поверхности грунта - для приподнятого аналога (к таким сооружениям относятся, например, здания на подсыпках, дорожные насыпи и т.п.); такого же бруса, но конечной длины (параллелепипеда); вертикальной трубы конечной длины;

в) источники в форме горизонтальной трубы или бруса квадратного сечения, полностью находящиеся в грунте.

Учитывая относительно небольшие сроки возведения сооружений по сравнению с продолжительностью их службы, процесс установления граничных условий на поверхности контакта сооружения с грунтом (ограничивающей поверхности) можно считать практически мгновенным. При этом обычные для систем «атмосфера-грунт» или «инженерные сооружения - грунт» граничные условия третьего рода (когда задается температура теплоносителя) удается заменить на граничные условия первого рода (когда известной величиной является температура ограничивающей поверхности), обеспечивающие более простое решение.

Исследования института «Красноярский промстройниипроект» показали, что под центрами источников перечисленных конфигураций нестационарные температурные поля удовлетворительно подчиняются уравнению, выведенному Лахенбрухом [2] для центра круглого поверхностного источника.

                                      (1)

где θ и θ_пр - относительные (избыточные) температуры, соответственно нестационарная и стационарная;

 - число Фурье;

α - коэффициент температуропроводности;

y - глубина, считая от низа источника;

τ - время.

Это видно из табл. 1, в которой приведены значения θ для двух крайних из рассматриваемых случаев, когда верхнее граничное условие - температура θ = 1 - задана на части поверхности, имеющей форму круга и полосы. В первом случае температуры рассчитывались по формуле (1), во втором - по опубликованной в [13].

Таблица 1

Значения Q в зависимости от Q_пр и F₀ для центров полосы (числитель) и круга (знаменатель)

Однотипность нестационарных температурных полей под центрами источников различной формы и сравнительная простота описывающего их уравнения открывают большие возможности для решения задач о более сложными условиями однозначности. В частности, на основе уравнения (1) получено приближенное решение задачи типа Стефана для двух - и трехмерного случаев [4] (см. п.п. 3.6 - 3.7 Руководства), при единственном допущении, заключающемся в следующем: при отыскании производной глубины промерзания (оттаивания) по времени принято, аналогично [5] и по расчетам, что предельное температурное состояние в промерзающем (оттаивающем) грунте наступает практически мгновенно.

Основной исходной величиной в уравнении (1), отражающей влияние формы источника и нуждающейся в определении, является безразмерная стационарная температура θ_пр.

Решение стационарных температурных полей в Руководстве даны для поверхностных источников и горизонтальной трубы в грунте.

Стационарные температурные поля заглубленных и приподнятых источников определяются по формулам и графикам для поверхностных источников, только вместо координат реальной плоскости x, y подставляются координаты вспомогательной полуплоскости ξ, v на которой прямоугольные поперечные сечения заглубленных и приподнятых источников - бесконечного бруса, параллелепипеда и вертикальной трубы - конформно отображаются на поперечные сечения (линия на полуплоскости) своих поверхностных аналогов - полосы, прямоугольника и круга.

Решения представлены в окончательном, удобном для практического использования виде (графиков, таблиц), с промежуточными выкладками можно ознакомиться в [2 - 6]. Основные расчетные формулы даны в приложении 1. Графики для стационарных температурных полей в системе «термосвая-грунт» (конвективный теплообмен жидкого теплоносителя в термосвае учитывается методом эквивалентной теплопроводности) и нестационарных температурных полей получены путем обобщения результатов расчетов на электро- и гидроинтеграторе.

Графики для определения положения фазовой изотермы во времени (рис. 7 - 11) построены при допущении а₂/а₁ = 1 и  (λ₁, а₁, с₁ - коэффициенты тепло- и температуропроводности и теплоемкость в верхней зоне; λ₂, а₂, с₂ - то же в нижней зоне), что близко к действительности. Уравнение для общего случая дано в приложении 1.

В 4 - 6 разделах Руководства изложена методика определения исходных величин для расчета температурных полей грунта - составляющих внешнего теплообмена и теплофизических характеристик грунта (и коэффициента эквивалентной теплопроводности жидкого теплоносителя в термосвае). При составлении этих разделов ставилась цель - свести к минимуму количество исходных данных, определяемых в полевых и лабораторных условиях, т.е. упор делался на более доступные проектировщикам косвенные (расчетные) методы определения, основывающиеся на данных метеостанции и справочном материале. Методика определения некоторых вспомогательных данных вынесена в приложение. В приложении приводятся также примеры расчета, помогающие лучшему пониманию излагаемой методики.

1. ИСХОДНЫЕ И ИСКОМЫЕ ВЕЛИЧИНЫ, ИХ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ

Координаты параметры (размеры в м, время в час)

x и y - соответственно, горизонтальная и вертикальная координаты пространства, отсчитываемые от центра координат, расположенного под краем теплового источника (или под его центром - в задачах раздела 3 и в решении для горизонтальной трубы в грунте в разделе 2, а также в формулах приложения 1);

r - радиальное расстояние от центра источника (для круга и цилиндра) до точки, в которой определяется температура;

y_ц - глубина под центром источника, отсчитываетcя от его низа (за вычетом мощности слоя сезонного промерзания и оттаивания - для поверхностных источников);

ξ - глубина промерзания или для бесконечного цилиндра - радиус промерзания;

b и l - ширина и длина источника;

r₀ - радиус круга или цилиндра;

r_тр - радиус горизонтальной трубы;

r_из - внешний радиус теплоизоляционного покрытия;

h_из - толщина теплоизоляции;

h и h_тр - расстояние по оси у, соответственно, до низа заглубленного источника или, до центра горизонтальной трубы;

h_тер - общая длина термосваи;

h_п, h_н - длина подземной и надземной частей термосваи;

d₂, d₁ - диаметры большей и меньшей труб, образующих круглую щель;

τ - время;

τ_г - годовой отрезок времени, 8760 час.

Показатели температуры (°С)

t₀ - температура грунта за пределами источника (начальная температура - при расчете нестационарных температурных полей), устанавливаемая по наблюдениям за пределами зоны (или до начала) теплового влияния источника;

t_пр - предельная (стационарная) температура грунта в точке с заданными или искомыми координатами;

t'_пр - предельная температура с учетом геотермического градиента;

t_τ - нестационарная температура грунта в точке с заданными или искомыми координатами;

t_сг - среднегодовая температура в естественных условиях, определяемая разовым замером на глубине 10 м;

t_max - максимальная за год температура грунта;

t_п - температура ограничивающей поверхности (температура на контакте источника с грунтом), устанавливается согласно п.п. 4.1 - 4.6.

Климатические показатели

t_в - температура воздуха, град. (5.2)^*);

^*) Здесь и далее в скобках указан номер пункта, в которой изложена методика определения данного показателя.

A_м - годовая амплитуда колебаний температуры воздуха, град. (5.2);

В - радиационный баланс, ккал/м² · мес. (5.3);

LE - затраты тепла на испарение, ккал/м² · мес. (5.5);

Q_c = S + D - суммарная солнечная радиация, ккал/м² · мес. (5.3);

S и D - прямая и рассеянная солнечная радиация, ккал/м² · мес. (5.4);

A - альбедо поверхности, доли единицы (прил. III);

α_к - коэффициент конвективного (турбулентного) теплообмена, ккал/м² · час · град. (5.6);

E - интенсивность испарения, мм/сутки (5.5);

n_об - общая облачность, доли единицы, по данным метеостанций;

P - количество осадков, мм/декада, по данным метеостанций;

V_в - скорость ветра на высоте флюгера, м/сек, по данным метеостанций;

h_см, γ_сн - высота и плотность снежного покрова, м, по данным метеостанций с учетом п. 5.7.

Физические и теплофизические константы

λ, a, v_к и с - коэффициенты теплопроводности (ккал/м · час · град), температуропроводности (м²/час), кинематической вязкости (м²/час) и объемная теплоемкость; для грунтов, определяемые согласно п.п. 6.1 - 6.4, для прочих веществ и материалов - по справочникам;

C_ус, C_уз, C_ув - удельные теплоемкости частиц грунта, льда и воды (ккал/кг · град) (6.4);

γ_ск - объемный вес скелета грунта, кг/м³;

γ_у и γ - удельный и объемный вес грунта, кг/м³;

w_c и w_н - суммарная влажность и влажность за счет незамерзшей воды, доли единицы (6.3);

q - степень заторфованности (отношение веса торфа к весу всего грунта), доля единицы (6.4);

v - скорость движения хладоносителя, м/час;

G - степень водонасыщения, доли единицы (6.4);

γ_в и γ_л - плотность воды и льда, кг/м³ (6.4);

w_п - полная влагоемкость, доли единицы (6.4);

λ_э - эквивалентный коэффициент теплопроводности хладоносителя в термосвае, ккал/м · час · град (6.5);

λ_из, R_из - коэффициент теплопроводности, ккал/м · час · град и термическое сопротивление изоляции, м² · час · град/ккал, определяемые по справочному материалу;

λ_сн - коэффициент теплопроводности снега, ккал/м · час · град (5.7);

R_сн - термическое сопротивление снега, м² · час · град/ккал (5.7);

G_r - геотермический градиент, принимаемый по наблюдениям, или приближенно 0,03 град/м;

ρ - скрытая теплота фазовых превращений, воды 80 ккал/кг,

α - коэффициент теплоотдачи, ккал/м² · час · град (4.6).

Безразмерные обобщенные величины

 - предельная (стационарная) относительная температура, зависящая от формы источника;

 - нестационарная относительная температура;

 - число Фурье для источника любой формы, кроме бесконечного цилиндра;

 - число Фурье для бесконечного цилиндра (рис. 12);

 - число Фурье на графике рис. 7 - 11 (при K₀ = 0; );

 - критерий Нуссельта для цилиндра;

 - то же, для кольцевой щели;

 - критерий Прандтля;

 - критерий Рейнольдса;

 - то же, для кольцевой щели; H = y/h; μ = h/r₀; Г = x/h; η = r/r₀;  - критерий Коссовича;

   

Индексами «М» и «Т» в тексте обозначены теплофизические константы и температуры соответственно мерзлого и талого грунтов.

Индексами «МИН» и «ОР» - удельные теплоемкости соответственно минеральных и органических частиц грунта.

Цифрами 1 и 2 помечены теплофизические константы и температура в мерзлой и талой зонах в случае промерзания и, наоборот, - в случае оттаивания.

2. ПРЕДЕЛЬНЫЕ (СТАЦИОНАРНЫЕ) ТЕМПЕРАТУРНЫЕ ПОЛЯ ГРУНТА

2.1. Предельные температурные поля рассчитываются по формулам;

- для теплофизически однородного (мерзлого или талого) грунта

t'_пр = t₀ + θ_пр · (t_п - t₀) + Gr · y_п                                                  (2)

- для двухслойной среды из мерзлого и талого грунта;

в верхней (ближайшей к источнику) зоне

                                        (3)

- в нижней зоне

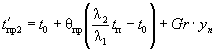                                                                                                                          (3¹)

здесь и далее y_п - глубина, отсчитываемая от поверхности грунта.

2.2. Величина θ_пр в выражениях (1) - (3') определяется с помощью формул в приложении 1 графиков на рис. 1 - 7 и в соответствии с указаниями п.п. 2.3 - 2.7.

2.3. Для поверхностных источников (полосы прямоугольника, круга), а также бесконечной горизонтальной трубы в грунте, изолинии температурных полей которых являются дугами окружностей (или по форме близки к ним), графики (рис. 1) даны только для осей симметрии (центров источника). Определение положения искомой изотермы в других точках плоскости x, y производится в таком порядке;

- по формуле (4) вычисляется радиус изотермы r_им

r_им = 0,5y_n(1 + δ)                                                           (4)

где δ - параметр равный:

 - для полосы и прямоугольника;

 - для круга;

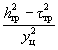 - для горизонтальной трубы

- описывается окружность радиусом r_им (искомая изотерма) из точки на оси симметрии, отстоящей от y_ц в сторону источника на величину r_им.

2.4. При действии нескольких (n) источников с одинаковой температурой ограничивающей поверхности θ_пр вычисляется по формуле

θ_пр = θ_пр(1) + θ_пр(2) + ... + θ_пр(n)                                               (5)

Величины θ_пр(1) - θ_пр(n) в уравнении (5) определяются по формулам приложения 1 или согласно п. 2.3.

Аналогично рассчитываются температурные поля под источниками сложной формы, если их удается представить совокупностью простых тел (прямоугольников, полос, секторов круга).

2.5. Если длина источника в два или более раз превышает ширину, а отношение ширины к глубине, на которой определяется температура, больше некоторой критической величины b/z^кр, зависящей от температурного перепада t_n - t₀ (табл. 2), величину θ_пр под центром источника с практической точностью можно принимать равной 1.

Таблица 2

Значение величины b/z^кр

Около границ таких источников θ_пр определяется по формуле

θ_пр = 0,5 ±                                                    (6)

или графику на рис. 1 как для полосы, но при δ = (x/y)² (x - отсчитывается от контакта между участками с отрицательной и положительной температурой). Знаки перед вторым слагаемым подбираются так, чтобы под источником (участком с температурой t_п) θ_пр лежала в пределах: 0,5 < θ_пр < 1; вне его 0 < θ_пр < 0,5.

В углах - величина θ_пр рассчитывается по формуле 3 прил. 1 как для сектора круга с центральным углом β = 0,5π.

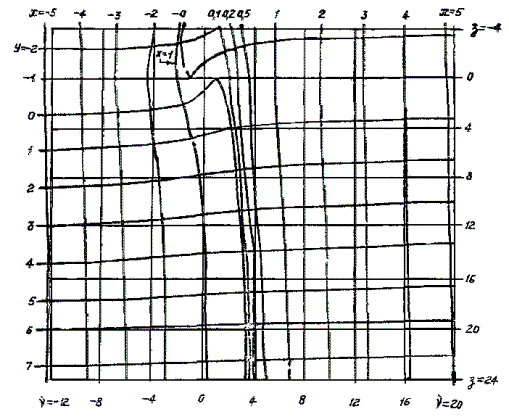
2.6. Предельные температурные поля заглубленных и приподнятых источников в форме бесконечного бруса, параллелепипеда, вертикальной трубы определяются также как и наземных (см. п.п. 2.2 - 2.5), только вместо X, Y и 0,5b в соответствующие формулы и графики подставляются координаты вспомогательной полуплоскости 1 + з, v и 1 + зв, найденные в зависимости от Г и Н с помощью графика на рис. 3, при этом величина зв, определяется при Г = 0,5b/h и H = 0. При расчете температурных полей заглубленных источников используется нижняя часть графика рис. 3 (v > 0), приподнятых - верхняя (v < 0).

Центр координат размещается под низом левого края источника.

2.7 На рис. 4 - 6 приведены графики для нахождения предельных температурных полей в системе «термосвая-грунт» для трех значений ε = λ_э/λ_м на конец холодного периода.

Величины ε могут изменяться от 1 до ∞. При ε = 1 величина θ_пр - 0,63θ_пр.кр. (θ_пр.кр. - предельная температура под источником в форме круга, определяемая согласно п.п. 2.2 - 2.3), при ε = ∞ величина θ_пр определяется как для вертикальной заглубленной трубы (п. 2.6). Для промежуточных значений ε предельные температуры ищутся в такой последовательности:

- при заданных значениях переменных H, μ и η определяется θ_пр для пяти значений ε (0, 22, 43, 86, ∞)

- по этим данным строится график зависимости θ_пр от exp(-0,01ε)

- с помощью указанного графика находится θ_пр для заданного значения.

Рис. 1 Стационарные (предельные) температурные поля под центрами (x = 0,5b, z = 0) поверхностных источников.

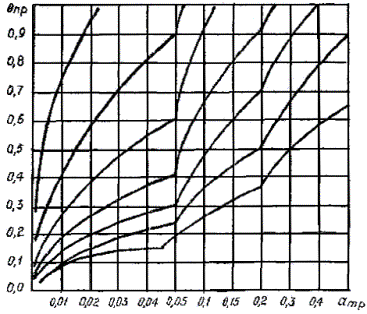
Рис. 2 Стационарные (предельные) температурные поля под центром (X = 0) горизонтальной трубы в области y = r_тр + h_тр; a_тр = (h²_тр - r²_тр)/y²

Рис. 3 Сетка для перевода координат X, Y в координаты з, v и обратно.

Рис. 4 Стационарные (предельные) температурные поля в системе грунт-термосвая при ξ = 85.

Рис. 5 Стационарные (предельные) температурные поля в системе грунт-термосвая при ξ = 43.

Рис. 6 Стационарные (предельные) температурные поля в системе грунт-термосвая при ξ = 22

Примечание. Размерные температуры в системе «грунт-термосвая» вычисляются по формуле (2), но вместо t_n в этом случае подставляется t_в - среднезимняя температура воздуха, вместо t₀ - t_max

2.8. Наличие термического сопротивления между сооружением и грунтом учитывается приближенно - удлинением координат глубины под сооружением (или логарифма относительного радиуса в пределах высоты цилиндрического источника) на величину эквивалентного слоя, т.е. в соответствующие формулы или графики вместо y и η подставляется

                                                            (7)

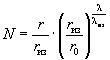                                                          (8)

3. НЕСТАЦИОНАРНЫЕ ТЕМПЕРАТУРНЫЕ ПОЛЯ ГРУНТА

3.1. Нестационарные температурные поля в грунтовом полупространстве при отсутствии фазовых превращений влаги (К₀ = 0) рассчитывается по формуле

t_τ = t₀ + θ · (t_п - t₀) + Gr · y_п                                                  (9)

3.2. Относительная температура θ в уравнении (9) для тепловых источников любой формы (за исключением бесконечного цилиндра) рассчитывается в такой последовательности:

- по п.п. 2.2 - 2.4, 2.6 находится θ_пр в точке с заданными координатами и затем - глубина под центром источника, в которой наблюдается найденное значение θ_пр;

- на этой глубине по графикам на рис. 7 при К₀ = 0 или, более точно, формуле (1), определяется величина θ, которая и будет искомой.

Рис. 7 Нестационарные температурные поля под центрами источников в форме полосы, прямоугольника, круга, их заглубленных аналогов, а также - горизонтальной трубы в грунте при θ_пр = 1 и θ_пр = 0,1.

Рис. 8 Нестационарные температурные поля под центрами источников в форме полосы, прямоугольника, круга, их заглубленных аналогов, а также - горизонтальной трубы в грунте при θ_пр = 0,9 и θ_пр = 0,2.

 

 

 

 

Рис. 9 Нестационарные температурные поля под центрами источников в форме полосы, прямоугольника, круга, их заглубленных аналогов, а также - горизонтальной трубы в грунте при θ_пр = 0,8 и θ_пр = 0,3.

Рис. 10 Нестационарные температурные поля под центрами источников в форме полосы, прямоугольника, круга, их заглубленных аналогов, а также - горизонтальной трубы в грунте при θ_пр = 0,7 и θ_пр = 0,4.

Рис. 11 Нестационарные температурные поля под центрами источников в форме полосы, прямоугольника, круга, их заглубленных аналогов а также - горизонтальной трубы в грунте при θ_пр = 0,6 и θ_пр = 0,5.

Рис. 12 Нестационарные температурные поля источника в форме бесконечного цилиндра (К₀ = 0).

Рис. 13 Графики для определения температур вечномерзлого грунта на любой отрезок времени года (пунктиром показаны графики для определения экстремальных температур).

Рис. 14 Графики для определения К в зависимости от Б

3.3. При расчете температурных полей, возбуждаемых цилиндрическими источниками с μ > 70 и (для горизонтального цилиндра) расположенных глубже 10 м, в плоскостях, отстоящих от торцов более чем на 4r₀ в сторону середины цилиндра, при определении θ допускается использовать решение для бесконечного цилиндра (рис. 12).

3.4. Расчет температурных полей, формируемых несколькими источниками, а также источниками сложной формы, осуществляема по формуле (5), только вместо предельных относительных температур θ_пр(1), θ_пр(2) ... θ_пр(n) подставляются нестационарные температуры θ₁, θ₂, ... θ_n, найденные согласно п. 3.2 - 3.3.

3.5. До глубины около 10 м температуры грунта испытывают сезонные колебания. Расчет температур однородного (талого или мерзлого) грунта в годовом цикле колебаний в естественных условиях, а также под зданиями и наземными сооружениями, основания которых охлаждаются атмосферным воздухом, либо подземными сооружениями, расположенными выше отметки 10 м, производится с помощью графика на рис. 11, при этом в случае расчета температур под зданиями и сооружениями вместо t_сг - подставляется значение t_пр, вычисленное согласно п.п. 2.2 - 2.5.

Учет сезонных колебаний при расчете температурных полей грунта, возбуждаемых тепловыми источниками в форме вертикального цилиндра конечной длины (в том числе - автономными холодильными устройствами), осуществляется путем прибавления к температуре вычисленной по формуле (1), величины Δt

Δt = (t_сг - t_max) ·                                                  (10)

здесь (τ - τ₀) - время работы теплового источника, час.

3.6. Нестационарные температурные поля в полупространстве при фазовых переходах влаги рассчитываются по формулам:

                                                      (11)

                                                          (12)

θ_1y, θ_2y и θ_1ξ, θ_2ξ в формулах (11) - (12) определяются согласно п.п. 3.1 - 3.3 при соответствующих значениях теплофизических констант. В выражение F₀ при вычислении θ_y подставляется заданная глубина, а при вычислении θ_ξ - глубина промерзания, если рассчитываются температуры промерзающего грунта, или оттаивания, если рассчитываются температуры оттаивающего грунта.

3.7. Глубина промерзания (оттаивания) под сооружениями различной формы определяется с помощью графиков на рис. 7 - 11 (а более точно, с помощью формулы в приложении 1).

Радиус промерзания (оттаивания) для источника в форме бесконечного цилиндра определяется в такой последовательности:

из соотношений (13) находятся параметры К и Б

                                                        (13)

- по графикам на рис. 14 определяется значения η = ξ/r₀ и затем ξ.

В выражение для θ при определении глубины или радиуса промерзания (оттаивания) вместо t_τ подставляется температура начала замерзания грунтовой влаги t_нз, для песчаных грунтов, а в первом приближении также и для глинистых, принимаемая равной нулю. Более точно величина t_нз определяется по методике, изложенной в приложении IV.

3.8. Учет термической изоляции между тепловым источником и грунтом во всех задачах нестационарной теплопроводности осуществляется приближенно, согласно п. 2.10.

4. ТЕМПЕРАТУРА ОГРАНИЧИВАЮЩЕЙ ПОВЕРХНОСТИ

4.1. При решении тепловых задач, связанных со строительным проектированием, обычно встречаются два типа ограничивающей поверхности - плоская и цилиндрическая.

4.2. Плоскую ограничивающую поверхность имеют крупные инженерные сооружения (жилые и общественные здания, склады, холодильники и т.д.), а также различного рода и назначения участки естественной поверхности с измененными условиями теплообмена (затененные от прямой солнечной радиации, с убираемым или уплотненным снежным покровом и т.п.).

4.3. Температуры ограничивающих поверхностей для инженерных сооружений (температура у поверхности пола для зданий с полами на грунте, либо у поверхности подвала или подполья) определяется по указаниям соответствующих глав СНиП или специальных методик и рекомендаций.

4.4. Температура поверхности участков естественной поверхности рассчитывается по формулам:

- среднегодовая температура

                                            (14)

- температура у поверхности грунта в теплый период года (с положительными температурами воздуха)

                                                        (15)

- температура у поверхности грунта в холодный период года принимается равной температуре воздуха.

В правые части формул (14) и (15) подставляются значения входящих величин соответственно средних за год и средних за искомый период (но не менее, чем за декаду).

4.5. Цилиндрической ограничивающей поверхностью обладают различного рода инженерные сети, трубопроводы, а также охлаждающие или нагревающие устройства.

4.6. Температура цилиндрической поверхности вычисляется по формуле

t_п = t₀ + θ' · (t_ср - t₀)                                                         (16)

где, кроме известных обозначений

t_ср - средняя температура тепло- или хладоносителя в трубе, величина которой должна быть известна из условий задачи;

θ' - относительная температура, определяемая по табл. 3 в зависимости от критерия B_i = α · r₀/λ.

Таблица 3

Зависимость θ' от B_i

Величина α в выражении для B_i находится из выражений:

- для круглой трубы

                                        (17)

(λ_x - коэффициент теплопроводности хладоносителя)

- для круглой щели между двумя коаксиально расположенными трубами

Nu_х = 0,015Re^0,8Pr^0,4(d₂/d₁)^0,25                                            (18)

Физические константы некоторых хладоносителей приведены в приложении II.

5. КЛИМАТИЧЕСКИЕ ПОКАЗАТЕЛИ

5.1. Влияние климата на температуру грунта опосредовано температурой ограничивающей поверхности. Входящие в формулу (14) величины отражают влияние основных климатических показателей - температуры воздуха и амплитуды ее колебаний, радиационного баланса, затрат тепла на испарение и конвективный (турбулентный) теплообмен, термического сопротивления снежного покрова на температурный режим грунта.

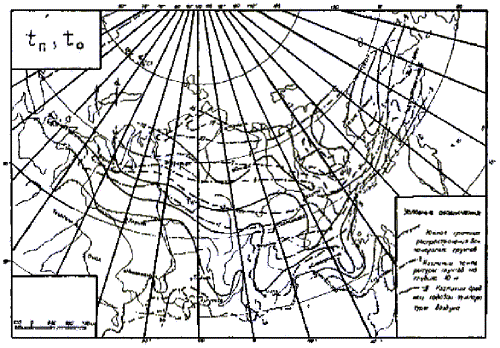
5.2. Температура воздуха и амплитуда ее колебаний устанавливаются по климатическим справочникам и ежегодникам. Среднегодовые температуры воздуха и грунта (левая часть формулы (14) показаны на схематической карте рис. 15.

5.3. Радиационный баланс за месяц вычисляется по формуле

B = Q_c(0,9 - 0,7А)² - 0,7 ккал/см² · мес.                                 (19)

Суммарная солнечная радиация определяется из выражения

Q_c = Q₀[1 - (1 - K_c) · n_об]                                               (20)

где K_c - коэффициент, показывающий какая доля солнечной радиации, приходящей на верхнюю границу облаков, доходит до поверхности земли.

Величины Q₀ и K_c находятся по табл. 4 и 5, а величина альбедо - по справочному материалу или приложению III.

5.4. Прямая солнечная радиация рассчитывается по формуле

                                                      (21)

5.5. Месячные суммы затрат тепла на испарение (ккал/см² · мес) в естественных условиях определяются из выражения

LE = 1,8E,                                                                 (22)

где Е - интенсивность испарения, мм/сут., устанавливаемая с помощью рис. 16.

Таблица 4

Среднеширотные значения суммарной солнечной радиации при безоблачном небе Q₀ ккал/см² · мес.

Рис. 15 Изолинии температур t_n и t₀ на территории распространения вечномерзлых грунтов.

Рис. 16 Зависимость испарения от температуры и давления воздуха (е, мб).

Таблица 5

Среднеширотные значения К_с

На участках с поверхностью, экранированной от прямого солнечного облучения, месячные затраты тепла на испарение вычисляются по формуле:

                                         (23)

где

t_в - среднемесячная температура воздуха

Q_c и D - суммарная и рассеянная солнечная радиация, ккал/см² · мес.

5.6. Для перевода месячных сумм солнечной радиации и затрат тепла на испарение с размерностями ккал/см² · мес. в систему размерностей ккал/м² · час, принятую в технике, результаты, полученные в соответствии с п.п. 5.3 - 5.5, умножаются на коэффициент 1,39.

5.7. Среднегодовые (сг) и среднемесячные (см) значения α_к ккал/(м · час · град) вычисляются по формулам

                                                       (24)

                                                     (25)

Вычисленные по формуле (24) среднегодовые величины α_к показаны на схематической карте (рис. 17).

5.8. Термическое сопротивление снежного покрова м² · час · град/ккал рассчитывается с помощью соотношений

R_сн = h_сн/λ_сн                                                             (26)

λ_сн = 0,87γ_сн + 0,018                                                     (27)

Рис. 17 Изолинии среднегодовых значений конвективного теплообмена

Рис. 18 Изолинии значений R_сн на территории с вечномерзлыми грунтами

Сетевые метеостанции дают величину максимальной за декаду высоты снежного покрова. Переход от максимальных декадных высот к среднемесячным осуществляется с помощью выражения

h_сн = 0,25(h₀ + h₁ + h₂ + 0,5h₃)                                         (28)

где h₀ - максимальная высота снежного покрова за предшествующую декаду (h₀ = 0, если определяется высота снежного покрова за первый зимний месяц);

h₁, h₂, h₃ - соответственно максимальные высоты снежного покрова за первую, вторую и третью декады месяца.

На рис. 18, 19 представлены схематические карты распределения величин R_сн рассчитанных по формулам (26) - (27) и  в области с вечномерзлыми грунтами.

6. ФИЗИЧЕСКИЕ И ТЕПЛОФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ

6.1. Теплофизические свойства грунтов характеризуются коэффициентами тепло- и температуропроводности (λ и С), а также удельной C_y или объемной C теплоемкостью. Эти величины связаны между собой соотношениями:

a = λ/C;                C = C_y · γ                                          (29)

6.2. Коэффициенты теплопроводности талого и полностью промерзшего грунта определяются по формуле

λ = λ^min + (λ^max - λ^min)G^φ = λ^min + (λ^max - λ^min)e^φlnG                        (30)

где λ^min, λ^max - коэффициенты теплопроводности при G = 0 и G = 1, а φ - безразмерный коэффициент, определяемые по табл. 7 в зависимости от параметра П = W_н/

Удельная теплоемкость талого грунта С_ут рассчитывается по формуле

                                   (31)

Удельные теплоемкости компонентов грунтового комплекса, входящие в уравнения для теплоемкости грунта, определяются по табл. 6.

Коэффициент теплопроводности λ'_м удельная теплоемкость промерзающего (оттаивающего) грунта С_ум рассчитываются по формулам:

λ'_м = λ_т[1 + (λ_м/λ_т - 1)(1 - W_н/W_с)]                                (32)

    (33)

Влажность за счет незамерзшей воды и производная этой величины от температуры зависят от температуры (см. приложение IV), но поскольку в уравнения для температурных полей они входят в виде констант, приходится идти на упрощение - брать в расчет средние значения W_н и dW_н/dt в температурном интервале значительных фазовых превращений. Среднее значение dW_н/dt в этом интервале для всех грунтов составляет минус 0,03 град.

Средние значения W_н принимаются по табл. 6.

Методика определения содержания незамерзшей воды в грунтах, в том числе засоленных, как функции от температуры, приведена в приложении IV.

6.4. Степень заторфованности грунтов и полная влагоемкость W_н в выражении для степени водонасыщения рассчитываются по формулам:

                                                          (34)

                                                (35)

где А (м³/кг) и В (безразмерный) - параметры, зависящие от состава минеральной части заторфованного грунта, принимаемые соответственно равными 3460 и 1,3 - для песчаных заторфованных грунтов, 3260 и 1,9 - для глинистых заторфованных грунтов.

Удельные веса составляющих грунтового комплекса приведены в табл. 6.

6.5. Эквивалентный коэффициент теплопроводности хладоносителя в автономных охлаждающих устройствах (термосваях) вычисляется по формуле

λ_э = 30λ_и(j + 0,4)Ф                                       (36)

Рис. 19 Изолинии значений Δt_сн на территории с вечномерзлыми грунтами

здесь, кроме известных обозначений

С_у, λ_и - удельная теплоемкость хладоносителя, ккал/кг · град и его истинная теплопроводность, ккал/м · час · град.

g = 9,8 м/сек² - ускорение силы тяжести.

А_р = 1/427 ккал/кг · м - тепловой эквивалент работы,

j - отношение надземной части термосвай к подземной.

Таблица 6

Удельные веса (кг/м³), теплоёмкости (ккал/кг · град), а также средние значения влажности за счет незамерзшей воды и параметра П (град^0,25) для типичных (незасоленных) грунтов (компонентов грунта)

Таблица 7

Значения λ^min, λ^max (ккал/м · час · град) и) и φ в зависимости от параметра П

ПРИЛОЖЕНИЯ

I. Формулы для расчетов температурных полей

а) стационарные (предельные) температурные поля под поверхностными источниками в форме:

1) бесконечной полосы -

2) прямоугольника -

3) круга

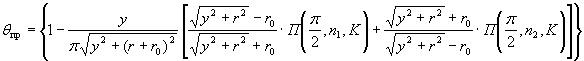
где   

 - полный эллиптический интеграл третьего рода (табулированная функция).

Для центра круга (β = 2π, r = 0) это уравнение значительно упрощается -

4) горизонтальной трубы в грунте -

б) нестационарные температурные поля грунта под центрами сооружений любой формы при отсутствии фазовых переходов -

5)

в) то же, при наличии фазовых переходов -

6) уравнение связи времени и глубины промерзания (оттаивания) под центром сооружений

где:

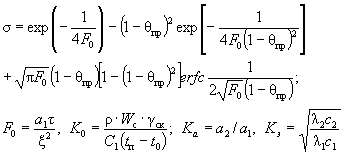
В выражение σ' в отличие от σ величина F₀ входит с множителем К_a.

Примечание: В формулах (5 и 6) глубина отсчитывается от низа сооружения, а его форма учитывается через величину θ_пр.

II. Физические и теплофизические свойства некоторых хладоносителей

Таблица 8

ПРИМЕЧАНИЕ: В таблице 8 приведены средние значения в интервале температур от -10 °С до -50 °С.

III. Значения альбедо (%) некоторых поверхностей

IV. Определение содержания незамерзшей воды в мерзлом грунте в зависимости от температуры

Содержание незамерзшей воды в грунте (отношение веса незамерзшей воды к весу сухого грунта) определяется по формуле

W_н = W_п · T^-0,35 = W_п · e^-0,35lnT                                                   (*)

где T = t/t_нз

t - температура грунта,

t_нз - температура начала замерзания свободной воды в грунте, определяемая по формуле:

                                         (**)

где Р - концентрация солей в грунтовой (поровой) влаге;

P_э и t_э - эвтектические значения концентрации и температуры, определяемые по табл. 9.

Таблица 9

Производная величины W_н по температуре, которая входит в формулу для расчета эффективной теплоёмкости, равна

                                               (***)

V. Примеры расчета

а) к разделу 2

1. Определить стационарную температуру грунта под длинным холодильником в форме заглубленного бруса при следующих исходных данных: t_п = -5, t₀ = -1, x = 3 м, y = 4 м, h = 6 м, b = 12 м (помнить, что начало системы координат в левом углу заглубления).

Находим безразмерные переменные

Г = 3/6 = 0,5; Н = 4/6 = 0,67; 0,58/h = 1

С помощью рис. 3 по найденным значениям Г, Н определяем значения

з = 3,8; зв = 5,7; v = 2,5

В формулу (1) приложения 1 вместо x подставляем 1 + з = 4,8 вместо 0,5b   1 + зв = 6,7, вместо y v = 2,5 тогда имеем

По формуле (2) основного текста вычисляем t_пр

t_пр = -1 + 0,76(-4) + 10 · 0,03 = -3,74

2. Определить стационарную температуру в системе «грунт - термосвая» при следующих исходных данных: h_п = 4 м, r₀ = 0,1 м, y = 1 м, r = 0,5 м, t_в = -21, t₀ = -1, ε = 86.

Определяем безразмерные переменные

μ = 40; η = 5, Н = 0,25.

По графику на рис. 4 находим искомую предельную температуру θ_пр = 0,12.

По формуле (2) вычисляем

t_пр = -1 + 0,12(-20) + 1 · 0,03 = -3,37

б) к разделу 3.

3. Определить нестационарную температуру грунта при исходных данных примера 1 и α_м = 0,004 м²/час; τ = 1200 час.

По графику на рис. 1 определяем относительную глубину, на которой θ_пр = 0,76 наблюдается под центром источника на вспомогательной плоскости с координатами з и v.

С учетом того, что зв = 5,7 (см. пример 1), величина v равна 6,7 · 0,35 = 2,35.

С помощью рис. 3 переводим величину v = 2,35 (при зв = 5,7) в y_ц; y_ц/h = 0,67, y_ц = 4.

Определяем F₀:

По графику на рис. 9 при К₀ = 0, θ_пр = 0,76 ≈ 0,8 и F₀ = 0,3 находим: θ = 0,23.

По формуле (9) вычисляем t(τ):

t(τ) = -1 + 0,23(-4) + 10 · 0,03 = -1,62

4. Определить время, за которое нулевая изотерма достигнет глубины y = 4 м под центром здания (b = 12 м, L = 19 м) с холодным подпольем (t_г = -3,5); необходимые для расчета исходные характеристики грунта: t₀ = +0,5; a_м = 0,004 м²/час; W_с = 0,1; γ_ск = 1600 кг/м³; С_м = 400 ккал/м³ · град.

С помощью графика на рис. 1 в зависимости от y/0,5b = 0,67 находим величину θ_пр: θ_пр = 0,6.

Вычисляем К₀ = 80 · 0,1 · 1600/(400 · 4) = 8 и θ = (0 - 0,5)/(-3,5 - 0,5) = 0,125.

По графику на рис. 11 находим P₀ = 6, откуда

τ = 6 · 16/0,004 = 2400 час ≈ 2,7 года

в) к разделу 4.

5. Определить температуру поверхности скважины (d₂ = 0,4), охлаждаемой холодным воздухом через трубу меньшего диаметра (d₁ = 0,1 м), коаксиально расположенную в скважине; λ_м = 1 ккал/м · час · град.

V = 5 м/сек, t_ср = -10, t₀ = -1.

Из формулы (18), подставив в нее указанные значения V, d₂ и d₁, а также значения v и a для воздуха, по приложению II находим величину коэффициента теплоотдачи: α = 13,5 ккал/м² · час · град.

Вычисляем критерий Био: B_i = 13,5 · 0,2/1 = 2,6

По табл. 3 находим значение θ': θ' = 0,86

По формуле (16) вычисляем температуру поверхности скважины

t_п = -1 + 0,86(-10 + 1) = -8,7

г) к разделу 5.

6. Определить величину радиационного баланса бетонного (светлосерого) покрытия за июль на 70° широте при общей облачности n_об = 0,6.

По таблицам 4 и 5 определяем Q₀ и K_c, а по приложению А:

Q₀ = 20,3 ккал/см² · мес; K_c = 0,5; А = 0,23.

По формуле (20) вычисляем Q_с:

Q_с = 20,3[1 - 0,5 · 0,6] = 14,2 ккал/см² · мес.

По формуле (19) находим величину радиационного баланса

B = 14,2(0,9 - 0,16)² - 0,7 = 7,1 ккал/см² · мес

7. Определить величину Δt_сн в районе Якутска

По схематической карте (рис. 19) находим Δt_сн = 4,8.

д) к разделу 6.

Определить теплофизические характеристики заторфованной глины со следующими характеристиками W_с = 0,43; γ_узг = 2,320 кг/м³, γ = 1620 кг/м³; t = -2, t_нз = -0,5.

С помощью формул (34), (35) и по приложению IV определяем исходные обобщенные характеристики:

g = 3260 : 2320 - 1,19 = 0,21

G = 0,43/0,48 = 0,89;

По формуле (*) приложения IV рассчитываем влажность за счет незамерзшей воды: W_н = 0,27.

Определяем параметр П = W_н/ = 0,27/1,19 = 0,23 и по табл. 6, в зависимости от величины этого параметра находим λ^min = 0,19; λ_т^max = 1,24; λ_м^max = 1,9; φ = 1,27.

По формуле (30) вычисляем λ_т и λ_м

λ_т = 1,1 ккал/м · час · град; λ_м = 1,6 ккал/м · час · град.

По формуле (32) рассчитываем коэффициент теплопроводности при t = -2

λ' = 1,1 · 1 + (1,45 - 1)(1 - 0,63) = 1,28 ккал/м · час · град.

По формулам (30), (33) с учетом (***) табл. 9 и выражения для объемного веса скелета грунта γ_ск = γ/(1 + W_c) определяем эффективную объемную теплоемкость

С = 1140[0,22 · 0,79 + 0,38 · 0,21 + 0,5 · 0,43 - 0,27(-0,5) + 0,02 · 80] = 2508 ккал/м³ · град.

ЛИТЕРАТУРА

1. Вялов С.С. Длительная прочность мерзлых грунтов при переменной нагрузке и температуре. Труды V Всесоюзного совещания-семинара по обмену опытом строительства в суровых климатических условиях. Т. 2, вып. 5. Тюмень, октябрь, 1968. Красноярск, 1968. (Институт «Красноярский промстройниипроект»).

2. Lachenbruch A.H. Three-dimentional heat conduction in permafrost beneath heated buildings. Geol. Surv. Bull. № 1052-В, 1957.

3. Лыков А.В. Теория теплопроводности. М., «Высшая школа», 1967.

4. Коновалов А.А. Метод определения температурных полей промерзающих или оттаивающих оснований зданий и сооружений. В сб.: Строительство в районах Восточной Сибири и Крайнего Севера, вып. 26. Красноярск, 1973. (Институт «Красноярский промстройниипроект»)

5. Порхаев Г.В. Тепловое взаимодействие зданий и сооружений с вечномерзлыми грунтами. М., «Наука», 1970.

6. Конюшенко А.Г., Коновалов А.А. К расчету стационарных температурных полей заглубленных сооружений. В сб.: Строительство в районах Восточной Сибири и крайнего Севера, вып. 26, Красноярск, 1973. (Институт «Красноярский промстройниипроект»).

7. Иванов Н.С. Тепло- и массоперенос в мерзлых горных породах. М., «Наука», 1969.

8. Пособие по проектированию оснований и фундаментов зданий и сооружений на вечномёрзлых грунтах. М., Стройиздат, 1969.

9. Руководство по расчетным способам определения прочностных деформативных и теплофизических характеристик мерзлых, промерзающих и оттаивающих грунтов. Красноярск, 1972. (Институт «Красноярский промстройниипроект»).

10. Будыко М.И. Тепловой баланс поверхности земли. Гидрометеоиздат. Л., 1956.

11. Константинов А.С. Испарение в природе. Гидрометеоиздат. М., 1963.

12. Кутателадзе С.С., Боришанский В.М. Справочник по теплопередаче. Госэнергоиздат. Л., - М. 1959.

13. К расчету температурных полей промерзающих и оттаивающих грунтовых оснований зданий и сооружений, в сб. «Строительство в районах Восточной Сибири и Крайнего Севера», вып. 29, Красноярск, 1974. (Институт «Красноярский промстройниипроект»)

СОДЕРЖАНИЕ